View Frustum Culling
作者:i_dovelemon
来源:CSDN
日期:2014 / 10 / 28
主题:View Frustum, Culling
引言
在前面的一篇文章获取View Frustum的6个面中讲述了如何根据View-Proj矩阵来获取View Frustum在世界坐标系中的6个平面。研究过场景管理的同学就会知道,在将图元数据传入到流水线之前,我们需要对数据进行组织。而场景管理通常就是进行这样的工作,通过场景管理,我们剔除(Culling)那些不在View Frustum中的物体,也就是在显示器中看不到的几何物体。读者可能会问,硬件不也会进行裁剪操作吗?是的,的确会这样。但是裁剪操作是发生在光栅化操作中。也就是说,很多的数据在最后光栅化的时候,被裁剪掉了,但是在前面的光照计算,纹理过程等等操作中都进行了,这明显浪费了资源,让系统做了不需要进行的工作。而今天讲解的View Frustum Culling就是来判断一个物体是否会显示在界面上,如果不显示,那么在应用程序阶段就将它剔除掉,这样就不用浪费资源来进行操作了。更彻底的,读者还可以实现那些被前面物体遮挡的物体剔除的算法。但这不再本文的讨论范围之内。好了,废话不多说,来讲解今天的内容吧!!!
AABB-Plane Intersecting
进行View Frustum Culling的关键技术在于进行AABB-Plane检测。在前面的文章中,我们获取到了6个平面,如果能够判断一个物体的AABB包围盒完全的在其中一个平面的负半空间中的话,就表明这个物体一定不再View Frustum中。这里,需要理解一个概念,什么是负半空间?
理论上,一个平面会将空间划分成为两个半空间,平面法向向量所指向的那个空间是正半空间,而另外一个空间被称为负半空间。我们在获取View Frustum一文中,获取的6个平面的法线都是指向View Frustum内部的。这就给我们的剔除提供了基础。所以,问题的关键就在判断一个AABB-Plane的位置情况。
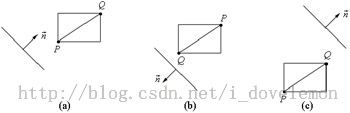
实现这样的检测,算法非常简单。我们根据要检测的平面法线的方向,在AABB盒上构造一个和这个方向最接近的一个向量,然后判断这个向量与平面的位置关系。看下面的图:
图中给出了三种基本的情况,PQ这条向量就是AABB盒上和平面上法线方向最接近的向量。从上图中可以得出下面的结论:
1.如果P点在平面所划分的正半空间内,那么AABB盒就在平面的正半空间内
2.如果Q点在平面所划分的负半空间内,那么AABB盒就在平面的负半空间内
3.如果P点在负半空间内,Q点在正半空间内,那么AABB就与平面相交叉
这三个结论,很显然通过观察就能够得到。
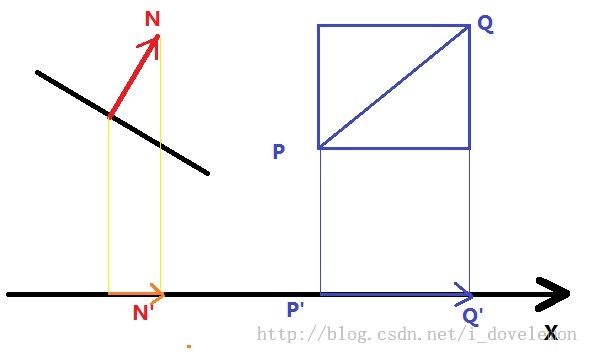
有了上面的结论,我们就是要获取PQ这两个点了。如何获取了?它的特征是和平面的法线方向最接近的值。如果我们单独看一个轴向上的情况,比如X轴向上。如图所示,一个平面的法线在X轴上的投影如下:
我们可以看到N在X轴上的投影为N‘,而想要让PQ的方向和N最接近,那么PQ这个向量在X轴向上的投影应该与N’一致,对吧!!!读者仔细观察下就会发现这样的事实。对于其他轴向上,此种事实同样出现。所以,我们的算法就是基于这个事实来给出的。如下是算法获取PQ这个向量的伪代码部分:
<span style="font-family:Microsoft YaHei;">VECTOR3 P, Q;
AABB a ;
Normal n;
if(n.x > 0)
{
//P.x < Q.x
P.x = a.min.x ;
Q.x = a.max.x
}
else
{
//P.x > Q.x
P.x = a.max.x;
Q.x = a.min.x ;
}
if(n.y > 0)
{
//P.y < Q.y
P.y = a.min.y ;
Q.y = a.max.y;
}
else
{
//P.y > Q.y
P.y = a.max.y ;
Q.y = a.min.y
}
if(n.z > 0)
{
//P.z < Q.z
P.z = a.min.z ;
Q.z = a.max.z ;
}
else
{
//P.z > Q.z
P.z = a.max.z ;
Q.z = a.min.z ;
}</span>
通过上面的代码,我们就可以得到PQ这个最接近平面法线方向的向量了。在有了这个向量之后,我们将Q点带入平面方程中,得出结果。如果结果为负,那么就表示Q点在平面的负半空间里面,也就是说上面的结论2成立,物体的AABB盒在平面的外面。还记的前面说过,我们获取的View Frustum的平面的正半空间是指向View Frustum内部的,也就是说如果在负半空间中的话,这个AABB盒就在View Frustum的外面了,不需要在对其他的面进行判断,我们就可以断定这个物体将不会被显示,能够被剔除掉。
好了,算法就介绍到这里。下面来看下完整的实现如何。
Demo
下面是测试这个算法的Demo。如果Cube还在View Frustuml里面的时候,就会在屏幕上写出Inside字样,如果在外面就会写出Outside字样。下面是算法的完整显示,同时给出了获取View Frustum的代码:
<span style="font-family:Microsoft YaHei;">void CubeDemo::draw()
{
drawCube();
//save the view proj matrix
m_ViewProj = m_Camera.viewproj();
//get the plane
D3DXVECTOR4 col0(m_ViewProj._11, m_ViewProj._21, m_ViewProj._31, m_ViewProj._41);
D3DXVECTOR4 col1(m_ViewProj._12, m_ViewProj._22, m_ViewProj._32, m_ViewProj._42);
D3DXVECTOR4 col2(m_ViewProj._13, m_ViewProj._23, m_ViewProj._33, m_ViewProj._43);
D3DXVECTOR4 col3(m_ViewProj._14, m_ViewProj._24, m_ViewProj._34, m_ViewProj._44);
m_Plane[0] = (D3DXPLANE)col2 ;
m_Plane[1] = (D3DXPLANE)(col3 - col2);
m_Plane[2] = (D3DXPLANE)(col3 + col0);
m_Plane[3] = (D3DXPLANE)(col3 - col0);
m_Plane[4] = (D3DXPLANE)(col3 - col1);
m_Plane[5] = (D3DXPLANE)(col3 + col1);
for(UINT i = 0 ; i < 6 ; i ++)
D3DXPlaneNormalize(&m_Plane[i], &m_Plane[i]);
D3DXVECTOR3 vcMin(-5,-5,-5), // AABB盒的min
vcMax(5,5,5), // AABB盒的max
_vcMin, _vcMax ; // _vcMin ==> P , _vcMax ==> Q
bool bOutSide = false ;
for(UINT i = 0 ; i < 6 ; i ++)
{
if(m_Plane[i].a > 0)
{
_vcMax.x = vcMax.x ;
_vcMin.x = vcMin.x ;
}
else
{
_vcMin.x = vcMax.x ;
_vcMax.x = vcMin.x ;
}
if(m_Plane[i].b > 0)
{
_vcMax.y = vcMax.y ;
_vcMin.y = vcMin.y ;
}
else
{
_vcMin.y = vcMax.y ;
_vcMax.y = vcMin.y ;
}
if(m_Plane[i].c > 0)
{
_vcMax.z = vcMax.z ;
_vcMin.z = vcMin.z ;
}
else
{
_vcMin.z = vcMax.z ;
_vcMax.z = vcMin.z ;
}
if(D3DXVec3Dot(&D3DXVECTOR3(m_Plane[i].a, m_Plane[i].b, m_Plane[i].c), &_vcMax) + m_Plane[i].d < 0)
{
bOutSide = true ;
break ;
}
}
RECT rect ;
rect.left = 10.0f;
rect.top = 400.0f;
rect.right = 100;
rect.bottom = 600 ;
if(bOutSide)
{
HR(m_pFont->DrawTextA(0, "OutSide", -1, &rect, DT_NOCLIP, D3DCOLOR_XRGB(0,0,0))) ;
}
else
{
HR(m_pFont->DrawTextA(0, "Not OutSide", -1, &rect, DT_NOCLIP, D3DCOLOR_XRGB(0,0,0)));
}
}</span>
下面是程序截图:
好了,今天到这里结束了!欢迎继续关注我的博客!!!