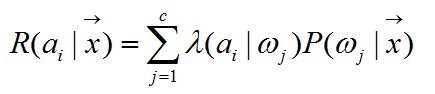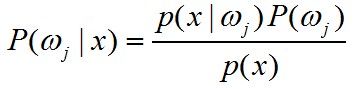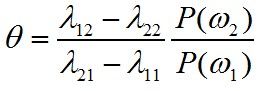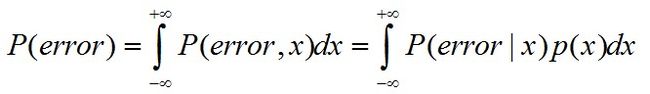极小化极大准则(minimax)
1、问题的提出
有时我们必须设计在整个先验概率上都能很好工作的分类器。也就是说,先验概率可能波动较大又或者先验概率在设计分类器时是未知的,那么我们要如何设定分类器的判决边界,使得无论先验概率以何种形式出现时,都可以将贝叶斯分类器的误差控制在一定范围,而不是大幅度的误差波动。
2、判决边界是什么?
先来看下面这张图
横轴为特征值x,纵轴为似然比。似然比就是似然函数的比值。假设有一个两类分类问题,两个似然比分别为p(x|ω1)和p(x|ω2),那么似然比就是p(x|ω1)/p(x|ω2)。
贝叶斯决策规则可以解释成如果“似然比超过某个阈值(θ),那么可判决为ω1类”。
3、为何可以依靠似然比及阈值来做决策?
由【此文】我们知道了风险是什么以及风险是如何计算的。根据如下的条件风险计算公式
我们可以计算两类分类问题
R(a1|x)=λ11P(ω1|x) + λ12P(ω2|x)
R(a2|x)=λ21P(ω1|x) + λ22P(ω2|x)
各个式子的含义:
R(a1|x)的意思是对特征值x采取a1行动所可能导致的风险。
R(a2|x)的意思是对特征值x采取a2行动所可能导致的风险。
λij的含义是将ωi类归到ωj类所导致的错误代价。
按照贝叶斯决策的意思,对特征值x要选择风险最小的一个行为来action。也就是说如果R(a1|x)<R(a2|x),那么将特征值x所在的样本判为ω1类。
进一步演绎这个不等式,得
λ11P(ω1|x) + λ12P(ω2|x) < λ21P(ω1|x) + λ22P(ω2|x)
λ11P(ω1|x) - λ21P(ω1|x) < λ22P(ω2|x) - λ12P(ω2|x)
(λ11 - λ21)P(ω1|x) < (λ22 - λ12)P(ω2|x) 【式 ①】
又根据贝叶斯公式
式①可以整理为
(λ11 - λ21)p(x|ω1)P(ω1) < (λ22 - λ12)p(x|ω2)P(ω2)
写成分数形式为
若将不等式的右边用θ替代,即
那么将有
这个不等式的含义就是:“当似然比大于θ时,也就是R(a1|x)<R(a2|x)时,因此判决为ω1”,得证。
4、如何确定阈值θ ?
阈值θ可以说是我们分类器的判决边界,那么怎样的θ才能满足我们在1中提出的问题,即在先验概率未知的情况下设定一个判决边界,该边界可以使总的风险的最坏情况界定在一定范围之内。
确定阈值的方法如下:
在似然函数固定的情况下,可以根据
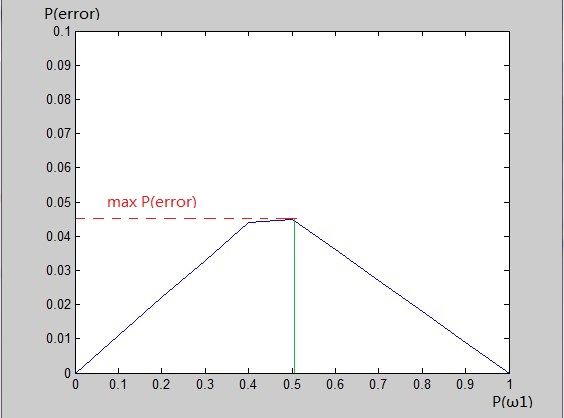
两个公式求出在x的取值域内,当P(ω1)取不同值时的曲线。如下图所示:
如图所示,当P(ω1)=0.5时,出现最大的贝叶斯误差。我们就将此P(ω1)值作为制订判决边界的参数来计算阈值θ。另一个参数P(ω2) = 1 - P(ω1)。λ11、λ21、λ22 、λ12均为已知。
P(error)的计算函数为:
function perror = getPerror(rate1,rate2) for index=0:10 pw1 = index/10; pw2 = 1-pw1; for x= 1:12 perror(index + 1) = 0; px = rate1(x)*pw1 + rate2(x)*pw2; pw1x = rate1(x)*pw1/px; pw2x = rate2(x)*pw2/px; if(pw1x < pw2x) perror(index + 1) = perror(index + 1) + pw1x * px; else perror(index + 1) = perror(index + 1) + pw2x * px; end end end
参数rate1为p(x|ω1),rate2为p(x|ω2)。
————————————————————————————
有朋友留言说太难懂。我在这里列一下文章的顺序,这一篇其实是贝叶斯决策的一个延伸,所以在此之前如果有贝叶斯的基础会比较容易看懂文章的内容。
基础的贝叶斯 -》
然后是它的例子-》
然后是贝叶斯决策 -》