Standford机器学习 线性回归Cost Function和Normal Equation的推导
1.线性回归CostFunction推导:
在线性回归中,Cost Function是![]() ,关于这个公式的推导,首先由一个假设
,关于这个公式的推导,首先由一个假设![]() ,其中
,其中![]() 满足高斯分布,
满足高斯分布,![]() .
.
那么![]() 根据
根据![]() 得出
得出![]() 在这里,把
在这里,把![]() 看成是随机变量,那么
看成是随机变量,那么![]() 服从高斯分布,
服从高斯分布,![]() ,对于给定的X,theta要估计y的分布是怎么样的,极大似然估计函数为:
,对于给定的X,theta要估计y的分布是怎么样的,极大似然估计函数为:
![]()
![]() 就是使得上式中的
就是使得上式中的![]() 最小,即
最小,即![]() 这个式子就是线性回归中的CostFunction J(theta),梯度下降的最终目标即是要最小化这个函数。
这个式子就是线性回归中的CostFunction J(theta),梯度下降的最终目标即是要最小化这个函数。
2. 线性回归中的NormalEquation的推导
Andrew Ng讲的推导过程有点复杂,不知道他的思维过程是怎么样的。下面我用线性代数的方法来推导下NormalEquation。
通常给定一个线性方程![]() ,要满足这个方程有解的条件是向量y在X的列向量张成的空间中。另外,对X的列向量进行线性变换即
,要满足这个方程有解的条件是向量y在X的列向量张成的空间中。另外,对X的列向量进行线性变换即![]() ,得到的向量一定是X的列空间中的。
,得到的向量一定是X的列空间中的。
现在这个问题中,样本的输入可以组成一个矩阵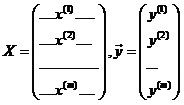 ,现在要求解
,现在要求解![]() ,找到这样的一个
,找到这样的一个![]() ,很明显,在大多数情况下这个方程是没有解的,原因是向量y不一定在X的列向量空间中。最小二乘法就是要在X的列向量空间中找到一个向量
,很明显,在大多数情况下这个方程是没有解的,原因是向量y不一定在X的列向量空间中。最小二乘法就是要在X的列向量空间中找到一个向量![]() ,使得这个向量和向量y的error最小。
,使得这个向量和向量y的error最小。![]() ,即
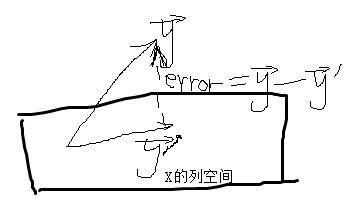
,即![]() ,请看下图:
,请看下图:
很明显,error最小的情况是找到y在X的列空间中的投影![]() ,它们的差值是最小的,那么
,它们的差值是最小的,那么![]() 就是我们要求解的,而且这个方程必定有解,那么如何找到这个投影呢?
就是我们要求解的,而且这个方程必定有解,那么如何找到这个投影呢?
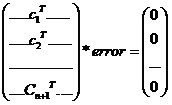
由于向量error和X的列空间是垂直的,所以error和X的所有列向量垂直,![]() ,ci是X的每一个列向量,所以
,ci是X的每一个列向量,所以![]() ,表示成矩阵的形式
,表示成矩阵的形式
所以![]() ,所以可以推导出
,所以可以推导出![]() ,X不是一个nbyn的矩阵,所以不能写成
,X不是一个nbyn的矩阵,所以不能写成![]()
其中![]() 可逆的充要条件是X的列向量不相关,这个可以自己推导下。所以在特征选取的时候不能选择一些线性相关的特征。
可逆的充要条件是X的列向量不相关,这个可以自己推导下。所以在特征选取的时候不能选择一些线性相关的特征。
Ps:上面的图太难看了,请见谅,不知道有没有好点的画图软件