【机器学习基础】理解为什么机器可以学习1——PAC学习模型
引言
自从下定决心认真学习机器学习理论开始,接触到很多基本问题,但其实都不是很理解,比如损失函数、风险函数、经验结构最小化、结构风险最小化、学习方法的泛化能力、VC维等,这些概念在学习中都纯属空泛的概念存在,我都不理解这些概念存在的意义。
为什么会存在这样的问题呢?我自己想了一下,有几个原因:首先,很多相关的书籍在讲授这些概念的时候,很少说这些为什么会有这样的概念问题,为解决什么问题引入的这些概念;然后,还有一些书,在简单表述了这些概念之后就立马挨个介绍算法了,遇到这样的书也会忽视这些基础问题的存在;最后,当初学者在遇到这些概念的时候,看到很多公式和抽象的表达方式,很容易产生挫败感,进而忽视了这些基础。
但是,我觉得这些问题还是很重要的。为什么这么说呢?原因如下:
1、理解这些问题有助于理解为什么机器可以学习,增强学习具体算法的信心,有助于深入进去;
2、理解这些基本问题并掌握基本的分析方法有助于分析具体学习算法的泛化能力;
举例
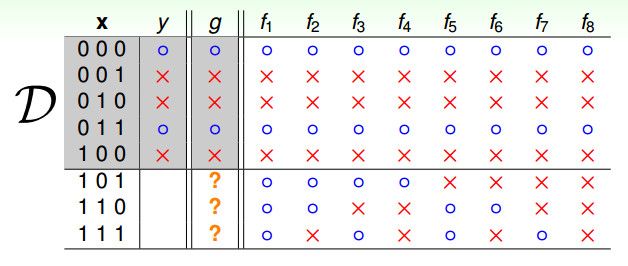
如图所示,输入为x,是一个三维数据,且元素都为布尔值,如果以D来做训练数据,那么要预测未知的情况,那请问当x为101,110,111的时候,预测输出y是什么呢?
我们看到图表中,会有8中不同的假设(hypothesis),所以我们无论预测是哪种输出,都有可能让我们的预测是完全错误的。这是不是就说明这种条件下,学习器是不可学习的呢?现在我们就从这个角度出发,看看如何训练我们的学习器,才能让学习器真正学到有用的知识,进而来产生有效的预测。
可能近似正确(probably approximately correct,PAC)学习模型
问题框架
这里我会简要描述一下我们要处理的具体问题。
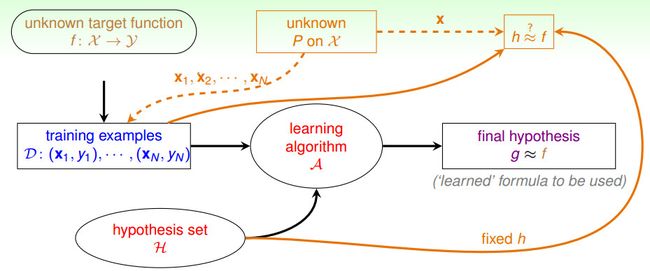
假定数据按照某概率分布P从X中随机产生,一般,D可为任意分布,并且它对学习型算法是未知的。对于P,所要求的是它的稳定性,即该分布不会随时间变化(不然我们就没有学习的意义了)。训练数据的由P分布随机抽取而产生x,然后x及其目标值(可以理解为y,标签)被提供给学习器
学习器在学习目标函数时考虑可能假设的集合H。
在观察了一系列训练数据后,学习器需要从假设集合H中得到最终的假设g,这是对未知的符合D分布的理想模型f的估计。
最后,我们通过精心挑选出来的假设g对X中新的数据的性能来评估训练器。
错误率
为了描述学习器输出的假设h对真实目标函数f的逼近程度,我们要定义两种错误率:
1、真实错误率(true error),也可以说是out-of-sample error,即样本之外,对于从任意分布中抽取的所有数据而言。
h的真实错误率是应用h到未来按分布P抽取的数据时的期望错误率
具体定义如下:
2、样本错误率(sample error),也可以说是in-sample error,即针对所训练的样本数据的。
因为h关于f的错误率不能直接由学习器观察到。学习器只能观察到在训练数据上h的性能如何,所以训练器也只能在此性能基础上选择其假设输出。我们用训练错误率(training error)来指代训练样本中被h误分类的数据所占的比例,以区分真实错误率。
那么,数据集合S的样本错误率为数据集合S中被h误分类的数据所占的比例。训练错误率就是当S为训练数据集合时的样本错误率。
PAC可学习性(PAC Learnability)
我们训练学习器的目标是,能够从合理数量的训练数据中通过合理的计算量可靠的学习到知识。
机器学习的现实情况:
1、除非对每个可能的数据进行训练,否则总会存在多个假设使得真实错误率不为0,即学习器无法保证和目标函数完全一致
2、训练样本是随机选取的,训练样本总有一定的误导性
为此,我们要弱化对学习器的要求:
1、我们不要求学习器输出零错误率的假设,只要求错误率被限制在某常数ε范围内,ε可为任意小。
2、不要求学习器对所有任意抽取的数据都能成功预测,只要求其失败的概率被限定在某个常数μ的范围内,μ可取任意小。
简而言之,我们只要求学习器可能学习到一个近似正确的假设,故得到了“可能近似正确学习”或PAC学习。
一个可PAC学习的学习器要满足两个条件:
- 学习器必须以任意高的概率输出一个错误率任意低的假设
- 学习过程的时间最多以多项式方式增长
对于PAC学习来说,训练样本的数量和学习所需的计算资源是密切相关的。如果学习器对每个训练样本需要某最小处理时间,那么为了使目标函数f是可PAC学习的,学习器必须在多项式数量的训练样本中进行学习。实际上,为了显示某输出空间的类别C是可PAC学习的,一个典型的途径是证明中每个C可以从多项式数量的训练样本中学习到,而后证明每个样本处理时间也限制于多项式级。
参考资料
机器学习, Tom M.Mitchell ,机械工业出版社
机器学习基石课程,林轩田,台湾大学
转载请注明作者Jason Ding及其出处