Data-Intensive Text Processing with MapReduce第三章(3)-MapReduce算法设计-3.2 PAIRS(对)和STRIPES(条纹)
3.2 PAIRS(对)和STRIPES(条纹)
在MapReduce程序中同步的一个普遍做法是通过构建复杂的键和值这样一个途径来使数据自然地适应执行框架。我们在之前的章节中涉及到这个技术,即把部分总数和计数“打包”成一个复合值(例如pair),依次从mapper传到combiner再传到reducer。以之前的出版物为基础【54,94】,这节介绍两个常见的设计模式,我们称为pairs(对)和strips(条纹)。
作为一个运行时的例子,我们关注于在大型数据上建立单词同现矩阵,这是语料库语言学和自然语言处理的共同任务。正式来说,语料库中的同现矩阵是一个在语料库中以n个不同单词(即词汇量)为基础的n×n矩阵。一个mij包含单词wi与wj在具体语境(像句子,段落,文档或某些窗口上的m词,m词是应用程序依赖的属性)下共同出现的次数。矩阵的上下三角形是同样的因为同现是一个对称关系,虽然一般来说单词之间的关系不必相对称。例如,一个同现矩阵M,mij是单词i和单词j同现的次数,它通常不能均衡。
这个任务在文本处理和为其它算法提供初始数据时很普遍,例如,逐点信息交互的统计,无人监管的辨别聚集,还有很多,词典语义的大部分工作是基于词语的分布式情景模式,追溯到1950年和1960年的Firth [55] 和 Harris [69]。这个任务也可以应用于信息检索(例如,同义词词典构建和填充),另外一些相关的领域例如文本挖掘。更重要的是这些问题代表着一个从大量观测值中的不相关的joint事件的分布的任务的特殊实例,统计自然语言处理的一个共同任务是MapReduce的解决方案。实际上这里展示的观念在第六章讨论最大期望值算法时也会用到。
除了文本处理,很多应用领域的问题都有相同的特性。例如,大的零售商会分析销售点的交易记录来识别出购买的产品之间的关系(例如,顾客们买这个的话就会想买那个),这有助于库存管理和产品在货架上的摆放位置。同样地,一个智能的分析希望分辨重复的金融交易,它将提供恶意买卖的线索。这节讨论的算法可以解决类似的问题。
很明显,单词同现问题的算法复杂度是O(n2), 其中n是词库大大小,现实中的英语单词全部加起来可能有10万多个,在web规模中甚至达到10亿个。如果把整个单词同现矩阵放到内存中,计算这个矩阵是非常容易的,然而,由于这个矩阵太大以致内存放不下,一种在单机上很慢无经验的实现是把内存保存到磁盘上。虽然压缩计数能够提高单机构建单词同现矩阵的规模,但是它明显存在限制伸缩性的问题。我们会为这个任务提供两个MapReduce算法来使其能适用于大规模的数据集。
1: class Mapper
2: method Map(docid a, doc d)
3: for all term w ∈ doc d do
4: for all term u ∈ Neighbors(w) do
5: Emit(pair (w, u), count 1) //出现一次发送一次计数
1: class Reducer
2: method Reduce(pair p, counts [c1, c2, . . . ])
3: s ← 0
4: for all count c 2 counts [c1, c2, . . . ] do
5: s ← s + c //统计出现的次数
6: Emit(pair p, count s)
图 3.8: 大数据集中计算单词的同现矩阵的伪代码
图3.8展示了我们称之为“pairs”的第一个算法的伪代码。像往常一样,文档的id和相关的内容组成输入的键值对。Mapper处理每一个输入文档和发送同现词对作为键1(即计数)作为值的中间键值对。这由两个嵌套循环来完成:外循环遍历每一个词语(pair中的左元素),内循环遍历第一个词语(pair中的右元素)的所有邻接词。MapReduce执行框架保证同一键的所有值都会在reducer中集合。因此,在这种情况下reducer只是用同一单词同现键值对获得文档中joint事件的绝对数量来进行简单的统计,这些值将作为最终键值对发送出去。每一个键值对相当于单词同现矩阵的一个值。这个算法说明了使用复杂的键来协调分布式计算。
1: class Mapper
2: method Map(docid a, doc d)
3: for all term w ∈ doc d do
4: H ← new AssociativeArray
5: for all term u ∈ Neighbors(w) do
6: H{u} ← H{u} + 1 //统计和w同时出现的单词的计数
7: Emit(Term w, Stripe H)
1: class Reducer
2: method Reduce(term w, stripes [H1,H2,H3, . . . ])
3: Hf ← new AssociativeArray
4: for all stripe H ∈ stripes [H1,H2,H3, . . . ] do
5: Sum(Hf ,H) //按元素进行统计Element-wise sum
6: Emit(term w, stripe Hf )
图 3.9:用stripes的方法来计算单词的同现矩阵, 注:element wise就是按元素进行运算,将两个不同矩阵内部的对应元素相乘
图3.9展示了另一个可选的方法---“stripes”方法。和pairs方法一样,同现词的键值对由两个嵌套循环来生成。然而,和之前方法主要的不同是,同现的信息首先被存放在关联数组H中而不是发送每一个同现词对的中间键值对。Mapper用词语作为key并把对应的关联数组作为value发送出去,每一个关联数组记录着某一个词语的相邻元素(如:它的上下文中出现的词语)的同现次数。MapReduce执行框架会使所有相同key的关联数组到reduce阶段一起处理。Reducer根据相同的key来进行统计运算(element-wise sum),积累的计数相当于同现矩阵中的同一个单元(cell)。最后的关联数组以相同的词作为主键发送出去。相比于pairs方法,stripes方法中每个最终键值对包含同现矩阵中的一行。
很明显,pairs算法相对stripes算法来说要生成很多键值对。Stripes表现得更加紧凑,因为pairs算法中的左元素代表着每一同现词对。Stripes方法则生成更加少而短的中间键,因此,在框架中执行时不需要太多的排序。但是,stripes的值更加复杂,也比pairs算法有着更多的序列化与反序列化操作。
这两种算法都得益于使用combiners,因为它们运行在reducers(额外和元素智能的关联数组的个数)的程序都是可交换和可结合的。然而,stripes方法中的combiners有更多的机会执行局部聚集,因为主要是词库占用空间,关联数组能在mapper多次遇到某个单词时被更新。相比之下,pairs的主要占用空间的是它自己和词典相交的空间,一个mapper观察到多次同一同现对时只能计数只能聚集(它和在stripes中观察一个单词的多次出现不同)。
对这两种算法而言,之前章节提到的in-mapper combining优化方法也可以对它们使用;因为这个修改比较简单我们把它留给读者作为练习。然而,上面提到的警告仍然有:因为缺少中间值的存储空间,pairs方法将有比较少的机会做到部分聚集。缺少空间也限制了in-mapper combining的效率,因为在所有文档都被处理之前mapper就有可能已经用完了内存,这样就必须周期地发送出键值对(更多地限制执行部分聚集的机会)。同样地,对stripes方法来说,它的内存的管理对于简单的单词统计例子来说更加复杂。对于常见的词语,关联数组会变得特别大,需要周期地清除内存中的数据。
考虑到每个算法潜在的伸缩性瓶颈是重要的。Stripes方法假定,在任何时候,每一个关联数组都要足够小来使之适合内存---否则,内存的分页会显著地影响性能。关联数组的大小受限于词典大小,而词典大小和文档的大小无关(回忆之前讨论过的内存不足问题)。因此,当文档的大小增加时,这将成为一个紧迫的问题---可能对于GB级别的数据还没有什么,但可以肯定未来将常见到的TB和PB级别的数据一定会遇到。Pairs方法,在另一方面,没有这种限制,因为它不需要在内存中保存中间数据。
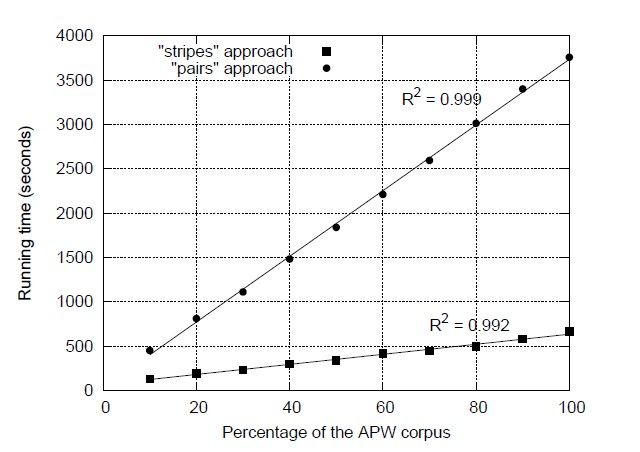
鉴于此讨论,那一个方法更快呢?这里我们引用已发表的结果[94]来回答这个问题。我们在Hadoop中实现了这两个算法,并把它们应用在美联社Worldstream栏目(APW)中总计5.7GB的由2.27百万个文档组成的文档集中。在Hadoop中运行之前,文档集需先做下面处理:把所有XML标记移除,然后是用Lucene搜索引擎提供的基本工具来做分词和去除停止词。了更有效的编码所有分词都被唯一的整数代替为。图3.10对比了pairs和stripes在同一文档集中运行时的不同分数,这个实验是执行在有19个节点的Hadoop集群中,每个节点有一个双核处理器和两个磁盘。
这个结果说明了stripes方法比pairs方法要快很多:处理5.7GB的数据分别用666秒(11分钟)和3758秒(62分钟)。Pairs方法中的mappers生成26亿个总计31.2GB的中间键值对。经过combiners处理后,减少到11亿个键值对,这确定了需要通过网络传输的中间数据的数据量。最后,reducers总共发送1.42亿个最终键值对(同现矩阵中不为零的值的数量)。在另一方法,Pairs方法中的mappers生成6.53亿个总计48.1GB的中间键值对。经过combiners处理后,只剩0.288亿个键值对,最后reducers总共发送169万个最终键值对(同现矩阵中的行数)。像我们期望那样,stripes方法提供更多的机会来让combiners聚集中间结果,因此大大的减少了清洗(shuffle)和排序时的网络传输。图3.1.0也看到了两种算法展现出的高伸缩性---输入数据数量的线性。这由运行时间的线性回归决定,它产生出的R2 值接近1。
图 3.10: 使用不同百分比的APW文集作为实验数据测试pairs和stripes算法计算单词的同现矩阵所使用的时间,这个实验的环境是一个有着19个子节点的Hadoop集群,每个子节点都有两个处理器和两个硬盘。
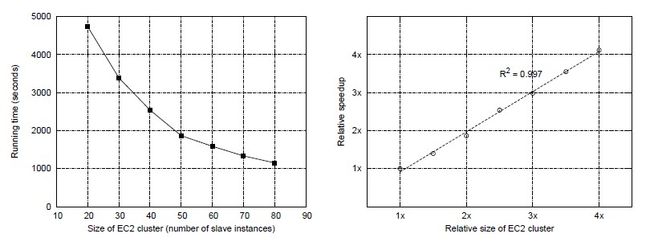
图 3.11:(左边)用不同规模的EC2服务器组成的Hadoop集群来测试stripes算法在APW文集中执行的时间。(右边)根据增加Hadoop集群的规模得到的标度特征(相对的运行速度的提升)。
额外的一系列实验探索了stripes方法另一方面的伸缩性:集群的数量。这个实验可以用亚马逊的EC2服务来做,它允许用户很快地提供聚群来,EC2中的虚拟化计算单元被称为实例,用户根据实例的使用时间来交费。图3.11(左)展示了stripes算法的时间(同一数据集,与之前相同的设置),在不同数量的集群上,从20个节点的“小”实例到80个节点的实例(沿着x坐标)。运行时间由实心方块标示。图3.11(右)重构同样的结果来说明伸缩性。圆圈标出在EC2实验中规模的大小和增速,关于20个节点的集群。这个结果展示了非常理想的线性标度特征(即加倍集群数量使任务时间加快一倍)。这由线性回归中R2值接近1决定的。
从抽象层面看,pairs和stripes算法代表两个计算大量观测值中的重现事件的不同方法。这两个算法抓住了很多算法的特点,包括文本处理,数据挖掘和分析复杂生物资料。由于这个原因,这两种设计模式可以广泛而且频繁地用在不同的程序中。
总的来说,pairs方法分别记录每个同现事件,stripes方法记录所有重现时间关心的调节事件。我们把整个词典拆分成b个部分(即通过哈希查找),wi的同现词会分成b个小的“子stripes”,与10个不同的键分开(wi; 1), (wi; 2) …(wi; b)。这是应对stripes方法中内存限制的合理方法,因为每个子stripes会更小。对b=|V|而言,|V|是词典大小,这与pairs方法是相同的。对b=1而言,这与标准的stripes方法相同。