压缩感知及实验分析
压缩感知及实验分析
摘要
压缩感知的主要内容有三个:信号x的稀疏表示;设计测量矩阵,在降维的同时,保证原始信号x的信息损失最小;设计信号恢复算法,利用降维后的观测值无失真地恢复原始信号x。根据压缩感知理论,基于Matlab平台,做了最简单的一维信号的压缩感知实验。
压缩感知原理
压缩感知的理论依据
<1> 如果信号x在某个正交基ψ上是k-稀疏的
说明:信号x可以通过正交基ψ分解得到对应的系数s,即x=ψ×s,系数s是k-稀疏的(指s中只含有k个非零值,或者只含有k个与众不同的值).
<2> 如果能找到一个与ψ不相关的观测基Φ(测量矩阵)
<3> 用观测基Φ观测x信号得到的观测值y:y=Φ×x
<4> 就可以利用最优化方法,从观测值y中高概率恢复x
最后,得到的压缩感知方程为:
y=Φ×x=Φ×ψ×s=Θ×s,Θ=Φ×ψ
其中,Θ被称为传感矩阵。由测量得到的y、选择的稀疏基ψ和观测基Φ,可以得到s的最优解s’,那么x的最优解x’就可以通过公式x’=ψ×s’计算出来。
信号的稀疏表示
<1> 稀疏表示的理论及数学描述
自然界存在的真实信号一般不是绝对稀疏的,但往往在某个变化域下近似稀疏,即为可压缩信号。所以,只要能够找到对应的正交基ψ,使得该信号可以有稀疏表达,就可以有效的进行压缩采样。
以一维信号为例,长度为N的信号x,存在一组正交基 ψT=[ψ1,ψ2,…,ψN] (其中 ψi 的维数是1×N,即ψ的维数为N×N),使得x=ψ×s,s的维数是N×1,s是属于k-稀疏的,其中k≪N 。
<2> 稀疏表示方法
经典的稀疏化方法有离散余弦变换(DCT)、傅里叶变换(FFT)、离散小波变换(DWT)等。如JPEG与JPEG2000的区别就体现在:JPEG采用DCT进行压缩,JPEG2000采用的是DWT ,而DWT要比DCT更加稀疏,因此JPEG2000有更高的压缩比。但本质上,都是将信号从一个域变换到另一个域上(即把坐标系进行旋转,将信号投影到不同的基上),从而获得信号的稀疏表示,用最少的系数来表示信号。信号不同,对应的最稀疏表达的基也会不同,对于一维信号小波基可能是最稀疏的,对于图像Curvelet和contourlet可能是最优的,而对于有些信号,则可能需要将几种基结合起来才是最优的,稀疏分解是找到信号的最稀疏最有效的表达,也是压缩的能力源泉。
目前,图像稀疏表示研究的另一个热点是信号在冗余字典下的稀疏分解,集中在两个方面:一是如何构造一个适合某一类信号的冗余字典;二是如何设计快速有效的稀疏分解算法。目前常用的稀疏分解算法大致可分为匹配追踪(Matching Pursuit)和基追踪(Basis Pursuit)两大类。
信号的观测矩阵Φ
<1> 观测矩阵的描述及设计目的
将原信号x(N×1)投影到观测矩阵(观测基)Φ(M×N)上得到观测向量y(M×1) 。其中,M≪N。
观测矩阵的设计目的有两个:将原信号x(N×1)通过投影降维到y(M×1);保证从y中恢复出x或者稀疏系数向量s(N×1)。
<2> 如何保证能从y中恢复x或s
测量矩阵Φ与稀疏基矩阵ψ的乘积需要满足有限等距性质(RIP),下面给出RIP的严格定义:
如果的M×N的矩阵Θ满足
那么就称矩阵Θ以参数 δk∈[0,1) 满足k阶有限等距性质,简记为Θ ∈RIP(k,δk) 。其中集合T的势 |T|≤k,ΘT 为保留Θ中子列索引集合T对应列构成的子矩阵。
Candes E J, Romberg J, and Tao T.等给出的精确重构k-稀疏信号x的充分条件为: δ2k≤√2−1 ,Cai T T, Wang L, and Xu G W等进一步得到恢复k-稀疏信号的充分条件为: δk≤0.307 。
RIP性质保证了传感矩阵Θ不会把两个不同的k-稀疏信号映射到同一个集合当中,这就要求从中Θ中抽取的任意不大于k个的列向量构成的矩阵是非奇异的。如果稀疏基ψ和观测基Φ不相关,则很大程度上保证了传感矩阵Θ的RIP性质。CandeS和Tao等证明:独立同分布的高斯随机测量矩阵可以成为普适的压缩感知测量矩阵。 所以,一般用随机高斯矩阵作为观测矩阵。目前常用的测量矩阵还有随机贝努利矩阵、部分正交矩阵、托普利兹和循环矩阵和稀疏随机矩阵等。
信号的重构算法
先通过式子 y=Φ×x=Φ×ψ×s 的逆问题求解稀疏系数向量s,然后再由式子 x=ψ×s 恢复出信号x。稀疏系数向量s的重构问题可以等价为求解矩阵列向量的稀疏组合问题,最直接的方法是通过L0范数求解最优化问题:
从而得到稀疏系数向量s的估计s’,s’即为上式中求出的满足条件的α。然而,上式的求解是一个非确定项难问题(NP-hard),往往L1最小范数与L0最小范数在一定条件下具有等价性,可得到相同的解,那么上式就可以转化为L1最小范数的最优化问题:
L1范数最小化是凸优化问题,可以将求解过程转化成线性规划问题,又被称为基追踪(BP),常用的实现算法有:内点法和梯度投影法。内点法速度慢、结果准确,而梯度投影法速度快、结果不如内点法准确。
目前,压缩感知的重构算法主要分为两大类:一是贪婪算法,通过选择合适的原子并经过一系列的逐步递增的方法实现信号矢量的逼近,此类算法主要包括匹配跟踪算法、正交匹配追踪算法、补空间匹配追踪算法等;二是凸优化算法,通过把L0范数放宽到L1范数由线性规划求解,主要包括梯度投影法、基追踪法、最小角度回归法等。
压缩感知实验分析
<1> 实验结果
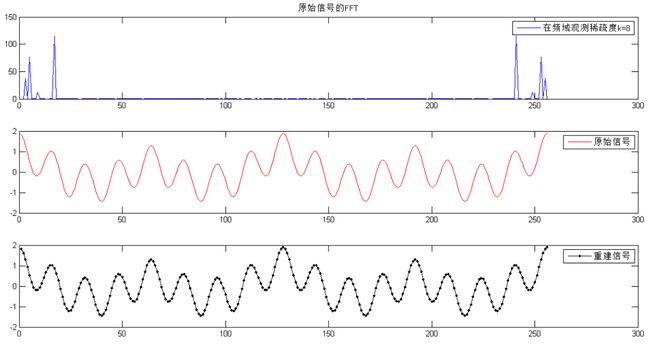
重建信号与原始信号的对比如图,重建误差计算为 3.2988×10−15 。
<2> 实验步骤-流程
1) 选择合适的k-稀疏信号x
实验中选取的原始信号是一个由4个不同频率正弦信号叠加得到的信号为:
其中 n∈[1,N],N=256,f1=50,f2=100,f3=200,f4=400,fs=6400 。
由FFT结果可以知道原始信号在频率域上是稀疏的,即原始信号为k-稀疏信号,k=8。
2) 选择适合的测量矩阵Φ,观测得到测量值y
实验中选择的测量矩阵为高斯分布白噪声, Φ(M×N),M=64 ,其中M的取值应当满足 M≥k×log(N÷k)≈28 。由公式y=Φ×x,得到测量值y。此时y向量是M维的,从而实现了将256数据长度的x压缩(降维)至64长度的y。
3) 得到正交稀疏基ψ、传感矩阵Θ
因为选取的原始信号在频率域上是k-稀疏的,那么就有: x=ψ×s ,其中ψ(N×N)为傅里叶反变化矩阵,s为稀疏系数向量,也就是fft的结果。然后计算得到传感矩阵 Θ(M×N)=Φ×ψ 。
4) 正交匹配追踪法(OMP算法)得到逼近值s’
算法思想:贪婪迭代,每次都做出当前最好的选择,而不对整体加以考虑。
算法流程
i) 初始化残差 r0=y 、增量矩阵 Ω0 为空集、指标集 ID0=∅
ii) 找到满足下述最优化问题的指标λ_t,求出最大投影系数对应的位置,即找到一个其标记看上去与收集到的数据最相关的小波
iii) 扩充指标集ID和增量矩阵Ω
iv) 解如下最小二乘问题,
v) 从Θ中剔除当前所选中的具有最大投影系数对应的列,避免重复。计算新的信号估计和残差
vi) 迭代次数t=t+1,若 t<k 返回步骤2(一般可迭代2k次,对于舍弃其他小的系数值,而构成的k-稀疏度,多迭代可以使误差更小,在本例中,迭代了2k次,由于是理想周期函数抽样,所以后k次迭代得到的s’对应的值都是0)
vii) 重建s’,s’中的第 λj 个元素元素的值等于α_t中的第j个元素,其余为0
5) 通过公式:x=ψ×s,重建原始信号x’
由前面介绍,ψ为傅里叶反变换矩阵,那么x’=ψ×s’。
2015-9-19 艺少