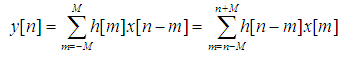Savitzky-Golay 滤波器

Savitzky-Golay滤波器（通常简称为S-G滤波器）最初由Savitzky和Golay于1964年提出，发表于Analytical Chemistry 杂志。之后被广泛地运用于数据流平滑除噪，是一种在时域内基于局域多项式最小二乘法拟合的滤波方法。这种滤波器最大的特点在于在滤除噪声的同时可以确保信号的形状、宽度不变。

信号的最小二乘平滑

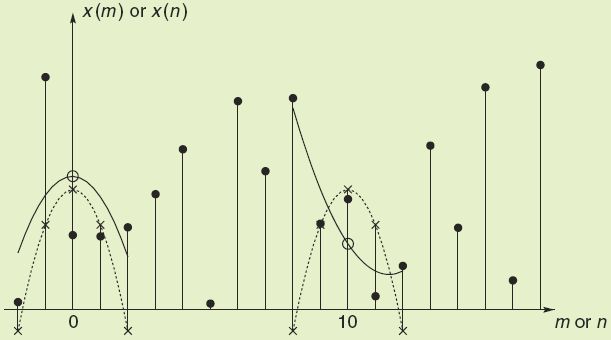
信号的最小二乘平滑的基本思想可以通过图1来说明。

图 1 信号的最小二乘平滑的示例

一列数据x[n] 在图中用实心的圆点来表示。考虑一组以n=0为中心的2M+1个数据。我们可以用如下的多项式来拟合它。

所以我们只需要获得拟合多项式的常数项。Savitzky和Golay 发现计算a0相当于对原始数据进行一次FIR 滤波。也就是说可以利用卷积运算来实现。

也可以说是对输入数据进行了加权平均。图1中x 表示的就是加权系数。下面就来说说如何获得a0。

由基本的微积分知识可知，若要ε最小，ε对各个参数的偏导数都应为0，也就是：

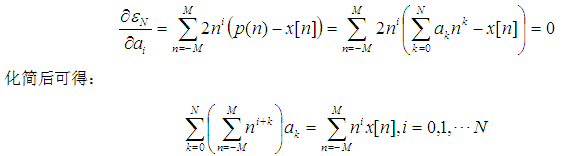
我们引入一个（2M+1）行（N+1）列的辅助矩阵A。

载设一个辅助矩阵B，使得：

H 的第一行行向量就是我们要求的卷积系数。从上面的推导可知，H 是与x无关的，只由N和M来决定。比如N=4，M=5时。用下面的Maxima 代码可以获得A，B和H。

可以看到，用Maxima来计算SG 滤波器的系数是非常方便的。还有另外一种方法只计算H 的第一行，其基本思想如下。首先选取一个特殊的x=x’，利用 x 可以算出a’，这一步就是普通的多项式拟合，各种数学软件都能计算，不需要从矩阵A 开始构造。然后用a’来计算H的第一行。具体的说就是取x’ 为单位冲击序列。

*号部分是我们无法确定，这一部分我们也不需要确定。我们再将H 的表达式写出来。

下面仍然以N=4，M=5为例，给出Matlab 代码：

x=[zeros(1,5),1,zeros(1,5)]
a=polyfit([-5:5],x,4)
polyval(a,[-5:5])

当然，利用Maxima 同样可以计算，下面给出代码：

至此，SG Filter 的构造问题就解决了，关于SG滤波器的性质，等我有空时再写一篇博客详细介绍。