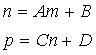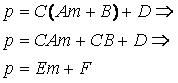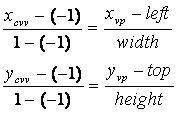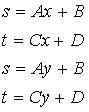深入探索透视纹理映射（上）

-潘宏
-2010年5月3日

-本人水平有限，疏忽错误在所难免，还请各位数学高手、编程高手不吝赐教
-email: [email protected]

 

在这篇文章中，我们将探讨图形流水线中另一个复杂的主题——透视纹理映射（Perspective Texture Mapping）。你可能听说过仿射纹理映射（Affine Texture Mapping）（没听过？没关系，我会让你理解的），并且知道在大多数情况下仿射的已经足够了，但如果不能很好的理解透视纹理校正，可能某一天当你在3D空间中移动相机的时候，突然发现你所熟悉的一些场景开始在屏幕上剧烈地“蠕动”，你很有可能意识不到美术在导出模型的时候不小心关闭了透视校正开关。如果不信，请马上关闭你渲染器中的透视校正开关，然后一边移动相机一边欣赏场景（没感觉到？场景中的面是不是太小了？相机是不是离物体太远？）。

这个主题比较复杂，因此我准备分两篇文章来分析这个主题。第一篇介绍必要的基础知识以及仿射纹理映射的基本概念。第二篇引出仿射纹理映射存在的问题以及如何实现透视校正。最后将给出一些实现一个完整透视纹理映射器的参考（来自于Chris Hecker）。这对于需要自己实现软件光栅器以及希望打下坚实图形学基础的人来说是必不可少的材料。希望你能够坚持看完并自己动手开始实现它。

透视纹理映射甚至比透视投影变换更另初学者觉得神秘莫测。这个阶段处于图形流水线的下游，是一个牵扯面很广的处理过程，需要你对图形流水线有一个比较清楚的认识，幸好我们已经对透视投影有了一个细节层次的认识，我们已经理解了顶点如何变换到裁剪空间，并进行透视除法（如果你对这些还不是很了解，请参考《深入探索透视投影变换》一文）。我们将从透视投影之后开始探索，目的是让流水线初学者有一个清晰的认识，能够了解流水线是如何过渡到透视纹理映射阶段的。由于透视纹理映射的推导比较复杂，我们仍然在开始的时候给出一些重要的数学技巧，目的是为了让我们在后面的推导过程中轻松一些。首先来看一个比较重要的理论。

 

线性关系与线性插值

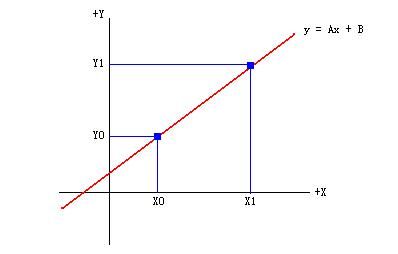
在2D平面上，一条直线可以表示为斜截式：y = Ax + B。这个形式也表示变量x和y是线性关系。也就是说，只要参数A和B定下来，则x和y就有了一个固定的对应关系，有一个x，在直线上就有唯一一个y和它对应。更具体地说，比如x的范围是[X0, X1]，则对应的y范围就是[Y0, Y1]。如下图所示

 

 

这同时也是一个简单的线性插值的关系。我们从《深入探索透视投影变换》中讲到的线性插值公式来看：

 

  

上面的式子表明，线性关系的两个变量可以进行线性插值，线性插值公式和直线公式其实是一致的。也就是说，如果两个变量是线性关系，就可以对它们进行线性插值，从而从一个变量x得到另一个变量y。为了更直观的说明这个理论，我举一个例子：假设我们在研究图形学的某个领域时发现有两个变量m和n，它们满足线性关系

 

 

 

则它们可以在平面上用一条直线表示出来，同时，对于m的一个区间M=[M0, M1]，n的一个区间N=[N0, N1]中的每一个值和M中的值都是一一对应的。则我们通过一些输入操作，得到了M=[23.4862, 100.3975]，以及N=[0.5836, 0.9762]，则通过循环取遍M中的任何一个值m，我们都可以通过线性插值公式得到相应的n。就像下面的程序这样：

 

// 假设m0和m1是m的取值区间

// n0和n1是n的取值区间

// mstep是m插值的步长

double m0 = 23.4862;

double m1 = 100.3975;

double n0 = 0.5836;

double n1 = 0.9762;

double mstep = 0.1266;

double A = (n1 – n0) / (m1 – m0);

double B = n0 – A * m0;

double m, n;

for( m = m0; m <= m1; m+=mstep)

{

       n = A * m + B;

       // 做其他处理

       // …

}

 

上面的代码就实现了对n基于m进行线性插值。此外，线性关系还有传递性。比如，我们有两个线性关系：

 

 

 

 

则通过把n带入第二个式子，有

 

 

 

则我们得到结论：如果m和n是线性关系，同时p和n也是线性关系，则m、n以及p互相都为线性关系。希望你能够记住这些线性理论，因为——我们后面将会用到它们。

 

视口变换（Viewport Transform）

我们在《深入探索透视投影变换》一文中分析了当前流行的图形API所使用的透视投影矩阵的构造原理。在文章结束的时候，我们构造出了透视投影矩阵，并可以把它应用于观察空间中的顶点。对顶点实施透视投影变换之后，顶点变成了4D的齐次坐标的形式，从而进入了固定流水线中的裁剪空间，等待进行图元装配（Primitive Assembly）并针对图元进行CVV裁剪。裁剪之后的图元顶点接下来即将“遭受”的处理就是透视除法。透视除法把顶点从4D的齐次形式再次变回3D的普通形式，变化之前由于采用了精心设计的透视投影矩阵进行过处理，因此能够在裁剪过程中“幸免于难”的顶点以及新生的顶点都被“透视除法”成了归一化的设备坐标（NDC）。这个坐标系实际上就是规则观察体——CVV所包围的有限空间，在OpenGL的环境中x，y和z都在[-1, 1]的区间，是个正方体。接下来，顶点准备进入流水线下游阶段，开始进行屏幕处理。首先要做的一个事情，就是要把CVV中的顶点变到视口中。视口是你我可以在屏幕的窗口上看到3D图元的一个矩形区域。是它把虚拟的3D世界与真实的计算机屏幕连接起来。视口不是唯一的，可以有任意多个，每一个视口都可以有自己的观察姿态，可以用窗口坐标所表示的left，top以及width和height来定义，分别表示视口在窗口中的左上角坐标以及视口的长和宽（不同的API可能有些差别）。把顶点从CVV的xy平面上变换到视口中非常容易，采用的技术一点也不神秘，是什么呢？你可能已经猜到了，我们都讲了很多遍的——线性插值。把CVV中的x和y从[-1, 1]变换到视口的[left, left+width]以及[top, top + height]中，写出来就是：

 

 

 

其中x_vp和y_vp就是视口中的x和y，可以通过这两个公式计算出来。通过这样的处理，可以把所有图元的顶点都从CVV中变换到视口中来。此外，对于CVV中的z值，也可以变换到视口中来，虽然很多渲染器都直接保留CVV中的z值，但仍然可以通过线形插值把[-1, 1]中的z变换到视口自己的z范围[z_min, z_max]中，各个API都提供了这样的方法，这里就不具体说明了，因为它和我们这次的主角——透视纹理映射——关系不太大。

    图元顶点们经过了视口变换后，尽管统统都进入了窗口坐标中，但这个时候还看不到。为了能够看到窗口中的图元，要把图元进行光栅化——从连续的虚拟空间变换到离散的屏幕空间——对图元以及它们的所有属性进行过滤（Filter），以一定的规则变成像素的前身——片元（Fragment）。

光栅化（Rasterization）

目前的图形API都可以使用可编程的顶点着色器（Vertex Shader）和像素着色器（Pixel Shader）进行流水线上游（主要包括顶点变换、光照等等功能）和流水线下游（主要包括片元操作等等功能）的数据处理。但有两个地方始终是不可编程的——裁剪以及光栅化——它们被图形硬件自动完成。这两个部分被Benjamin Lipchak称为固定管线的粘合剂——连接顶点着色器和像素着色器的固定阶段。既然是不可编程的，它们的功能相对来说就比较单一了，前者的功能描述起来很简单——对图元进行CVV裁剪，去掉CVV外面的点，生成必要的新顶点，然后进行透视除法。而后者，我们开始在下面详细介绍。

经过了透视除法的顶点重新组合成图元，进行视口变换后，接下来就要经历光栅化阶段。在这个阶段中，图元被光栅化从而产生片元。图元是通过顶点定义的图形元素，包括点、线段、多边形、位图等等。片元是带有一系列属性的图像元素，比如位置、颜色、深度值、纹理坐标等属性。光栅化就是通过插值把一个图元过滤成能够在屏幕上表示它的一系列离散的片元，并通过片元操作把它们最终以像素的形式显示在帧缓冲中。过滤的意思就是通过样本重建信号，这里的意思就是通过对多边形在3D空间中的顶点以及相关属性的采样重新在屏幕上建立可见图像。而我们的主角——纹理映射，就是在光栅化阶段进行的。

下图展示了一个三角形在视口中被光栅化的过程，可以看到红色的点表示产生的片元，黑色的箭头表示光栅化的方向。

 

 

 

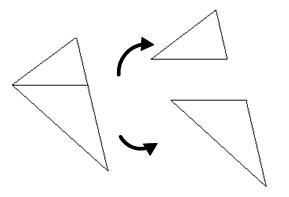
在实时图形学中，光栅化基本上都是基于对多边形进行扫描线转换（scan-line converting）。把一个三角形的三个顶点所包围的区域转换成和屏幕水平方向平行的由像素组成的一条条扫描线。对三角形进行光栅化，有两种使用比较多的方式：一种是André LaMothe在他那本大而全的《Tricks Of The 3D Game Programming Gurus》（3D游戏编程大师技巧）中所描述的平底或者平顶三角形的方式——把任意一个三角形分成一个平底和一个平顶三角形，然后进行扫描转换。如下图所示：

 

 

 

这样的话，只对平顶和平底三角形进行扫描线转换就可以了，降低了处理难度。另外一个方法就是Chris Hecker在他的震撼性系列文章《Perspective Texture Mapping》中使用的一般性方法——在一般三角形的扫描过程中，当遇到左边或者右边线段斜率变化的时候，比如下面这个三角形的红色线段的扫描线，上面的左线段和下面的左线段不是同一条线段，使用新的左线段来处理下半部分三角形。

 

 

 

实际上两种方法的主要差别在于是否把一个三角形提前分割成两个三角形。扫描线本身的处理都是一样的。在后面我们还要提到Chris Hecker和他的这些文章，他实现了一个性能非常高的软件透视纹理映射光栅器，尽管文章写于1995-1996年，但里面提到的知识以及用到的技巧非常棒，至今仍然可以被用在实时图形程序中。这里我们暂时先用André LaMothe的方法说明扫描线算法，因为它简单。现在我们来看一个简单的平底三角形的光栅化方法。

 

 

 

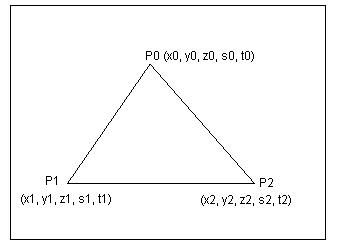
上图是视口中的一个平底三角形，可以看到它有三个顶点P0，P1和P2，分别有相应的x，y和z三个坐标，其中x和y是从NDC通过视口变换转换过来的，而z可能是NDC的数据，也可能是从NDC变成视口自己的z范围中。s和t就是每个顶点的纹理坐标值，它是一直从模型坐标带过来或者是通过API自动生成的，始终没有进行过处理。现在，我们就要把这个三角形做一个扫描线的转化。我们的老朋友又来了！谁呢？线性插值。我们通过下面的一个简单算法来看看插值过程：

 

double x, y, xleft, xright;

double s, t, sleft, sright, tleft, tright, sstep, tstep;

for(y = y0; y < y1; ++y)

{

       xleft = 用y和左边的直线方程来求出左边的x

       xright = 用y和右边的直线方程来求出右边的x

       sleft = 用y对s0，s1插值来求出左边的s

       sright = 用y对s0，s2插值来求出右边的s

       tleft = 用y对t0，t1插值来求出左边的t

       tright = 用y对t0，t2插值来求出右边的t

       sstep = (sright – sleft) / (xright – xleft);

       tstep = (tright – tleft) / ( xright – xleft);

       for(x = xleft, s = sleft, t = tleft; x < xright;

++x, s += sstep, t += tstep)

       {

               帧缓冲像素[x, y] = 纹理[s, t];

       }

}

 

上面的算法是一个最简单的线性插值纹理映射算法，一切都是基于线性插值的。在第一层循环的时候，我们通过左右两边的直线方程以及当前的y，计算出左边线段的x和右边线段的x，左边线段的s、t和右边线段的s、t。然后计算出s和t针对于的x变化量。第二层循环就是实际绘制扫描线，绘制的同时根据纹理坐标变化量更新s和t，然后把s和t所指向的纹理值赋给当前的插值像素点。这个过程使用了最简单的替换（replace）纹理混合方式，直接把纹理颜色替换到帧缓冲中当前的位置。而且在替换之前没有作任何的片元操作，比如深度测试、蜡板测试、Alpha测试以及混合等等。也没有考虑离散像素的填充规则，总之是一个最简单的光栅化框架。

在上面的插值中，我们做了一个错误的假设——纹理坐标s、t和屏幕x和y是线性关系。也就是说，我们假设

 

 

 

其中，s和t就是每个顶点的纹理坐标值，而x和y是视口中的屏幕坐标值。我们在这个假设的基础上进行了s和t对x和y的线性插值，这样的纹理映射方式就叫做仿射纹理映射。仿射纹理映射是应用在90年代的游戏开发中的主流方式（当前的很多游戏也在一些地方使用仿射方式），因为处理简单，所以性能比较高。你完全可以基于这个框架实现一个自己的仿射纹理映射器，并且在大多数情况下它都能“看起来正确”地显示（要让多边形和相机远离，让多边形显示尽可能的小）。但是，仿射纹理映射有一个最大的问题——它完全是错误的。我们将在下一篇文章中分析它为什么是错误的，并最终给出透视纹理映射的解决方案以及介绍Chris Hecker给出的非常牛的实现方法！下次见！