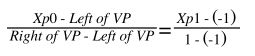深入探索3D拾取技术

-潘宏

-2013年1月

-本人水平有限，疏忽错误在所难免，还请各位高手不吝赐教

-email: [email protected]

-weibo.com/panhong101

3D拾取

在游戏中，玩家需要通过点击2D屏幕来选择3D物体，这个过程就是拾取（picking）。拾取是3D游戏必不可少的基本操作，它实现了玩家和游戏世界内对象的交互。

虽然拾取技术很基本，但它却迷惑了很多3D初学者。很多朋友都问过我关于拾取的细节问题，这让我觉得很有必要具体探讨一下该技术。 其实，拾取之所以让很多开发者感到复杂，主要原因在于它跨域了流水线的多个阶段，并且是逆流水线上行。另外，它是一个2D信息扩展到3D的过程，必须对信息做相应的扩展和额外的计算才能够得到正确的结果。下面我门具体分析一下这个技术。

水流线主要阶段分析

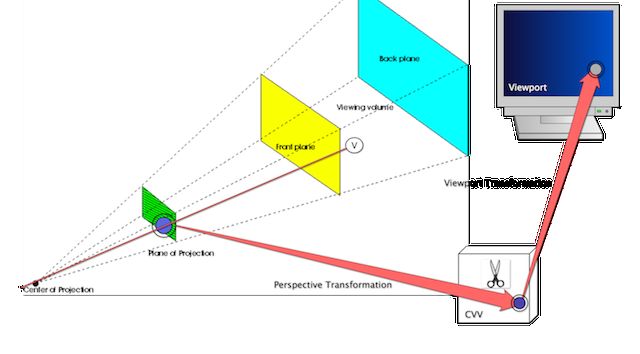
我们来直观地看一下从相机空间到viewport的变换图：

相机空间中的一个顶点v，经过透视变换后进入了CVV中。这个变换矩阵实际上完成了两个工作：

1）将顶点从3D空间投影到2D的投影平面（Projection Plane）上。

2）将投影平面上的2D投影点通过线性插值变换到齐次裁剪空间CVV中。

这些变换都通过透视矩阵一次完成（如果对此不是很了解，请参考《深入探索透视投影变换》一文）。 我之所以把这一步分解为两步，因为这对于分析拾取很重要。

顶点进入齐次裁剪空间并经过CVV裁剪，最终进行透视除法从4D齐次形式变回成3D形式。然后经过一个线性插值（被封装在视口（viewport）变换中），变换到viewport中，多个点以三角形的形式经过光栅化后被玩家看到。最后一步的点变换可以描述为：

3）将CVV中的点通过线性插值变换到viewport中。

分析了这个变换过程之后，我们知道了从相机空间开始实际处理点位置信息的操作，就是上面的三个步骤。这样，我们可以先把顶点从viewport中先变换回投影平面上，也就是我们可以先完成（2）和（3）的逆处理。这里我们不用考虑裁剪和透视除法这些操作，因为反推的时候，处于视口中的点，已经是经过裁剪后留下的有效点了，必定处于CVV内，也必定处于projection plane内！而且从viewport逆变换到projection plane，点一直保持2D形式。

picking的开始是玩家在屏幕上点击一个位置——这实际上是在viewport中进行了点击。我们通过响应玩家的点击事件，得到在viewport中的点击位置，记为P0（Xp0，Yp0）。然后我们把p0从viewport中线性插值到CVV中，得到P1（Xp1，Yp1）：

上面的线性插值（如果对线性插值公式不熟悉，请参考《深入探索透视投影变换》一文中的线性插值部分）公式在x方向上计算出了CVV中的P1，y方向的公式同理。接下来我们再把P1从CVV中变换到projection plane中，得到P2（Xp2，Yp2）：

y方向的计算同理。P2就是viewport中玩家点击的点在projection plane上所对应的位置。

目前来看很好。我们已经获得了相机空间中的投影平面上，玩家点击的位置。但目前的点是一个2D点——它处于投影平面上。玩家需要拾取的是一个3D对象，因此我们需要将2D信息拓展到3D中。

向3D世界拓展

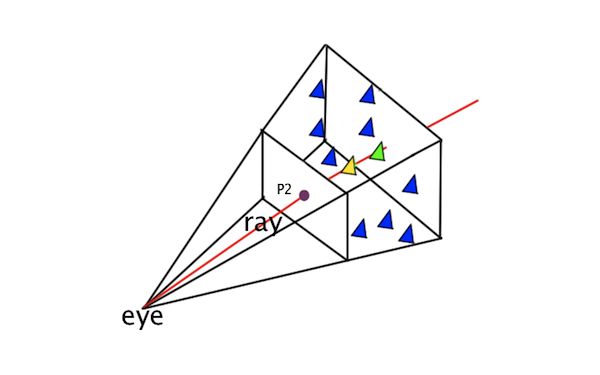
将2D的点信息拓展到3D空间进行picking，会使用射线（ray）进行。ray就是一端固定，另一端无限延伸的线性模型。如下图所示：

在相机空间中，红线标明的就是用于picking的ray。它的固定端就是eye的位置（也就是相机空间的原点），并且穿过我们刚刚求出来的projection plane上面的点P2。射线向空间无限延伸，第一个穿过的polygon应该就是picking到的结果。在图中，有两个polygon被picking到：绿色和黄色的。其中黄色的polygon是第一个被穿过的，因此picking操作返回的结果就是这个polygon。在实现中，我们一般有两种方式来表示一个ray：

struct Ray3D
{
	Point3D m_startingPos;
	Point3D m_penetratedPos;
};

struct Ray3D
{
	Point3D m_startingPos;
	Point3D m_direction;
};

第一种方式标明了ray的起始点m_startingPos和任意一个穿过点m_penetrated。第二种方式标明了ray的起始点m_startingPos和方向m_direction。这两种方式可以很方便的相互转换。

在有了ray的表示法之后，我们要做的就是判断ray是否和各个polygon产生了相交——这实际上是一个射线和三角形的相交判断算法。这种算法很普遍，很容易找到，这里我们不进行讨论。最基本的拾取算法（相机空间中）如下所示；

extern float ray_triangle_intersection( const Ray3D& ray, const Polygon& polygon );

GameObject* picking( const Point3D& P2, const std::vector< GameObject* >& objects )
{
	Ray3D ray;
	ray.m_startingPos = Point3D( 0, 0, 0 );
	ray.m_penetratedPos = P2;
	
	float minDistance = 10000.0; // Big enough
	GameObject* intersected = NULL;
	for( int i = 0; i < objects.size(); ++i )
	{
		GameObject* obj = objects[i];
		for( int j = 0; j < obj->number_polygons(); ++j )
		{
			Polygon* triangle = obj->get_polygon( j );
			float distance = ray_triangle_intersection( ray, *triangle );
			if( distance > 0.0 ) // Penetrated
			{
				if( distance < minDistance )
				{
					minDistance = distance;
					intersected = obj;
				}
			}
		}
	}
	return intersected;
}

这个暴力算法首先生成了相机空间中的ray，然后遍历所有的游戏对象，并遍历每个游戏对象的每一个多边形，用ray_triangle_intersection函数做射线交叉判断，如果返回正值，则证明穿插并表示ray起始点到穿插的距离，负值则表示没有穿插。函数判断每个穿插的多边形，保留最近的一个返回，如果没有任何穿插，则返回NULL。这里值得一提的是关于判断的优化问题。ray_triangle_intersection算法虽然可以优化，但对于一个规模较大的场景或者模型的polygon数量比较大的场景，通过这种暴力法遍历所有polygon，在效率上是不能够接受的。需要采用以下两种方式进行优化：

1）采用场景管理方法，用层次结构的方法提前剔除大量不在视线中的多边形。只留下视线中的多边形。

2）以包围体为单位进行ray相交判断，而不是三角形。比如包围盒、包围球等等，变成了ray和矩形、球体进行相交判断。一个游戏对象一般都可以分解为多个包围体。

除了上面的方法，还有很多其他高级的方式可以用于这种优化，这通常和你的游戏场景管理方法和3D对象表示方法有关。特别地，如果使用的是正交投影（Orthogonal Projection），则不需要使用ray，直接在平面上判断就可以了，这将退化为一个2D picking问题。

回到世界空间？

接下来的问题会有一些策略性。我们要决定的是picking在当前相机空间种进行还是在世界空间进行。我们已经处理了相机空间中的picking，但有一个问题：在程序中，我们一般不会保留相机空间中每个3D物体的位置，因此在这种情况下，我们会采用两个办法之一：

1）将ray用逆相机矩阵变换到世界空间中。

2）将物体用世界矩阵和相机矩阵变换到相机空间中进行picking，就如我们上面的处理方式。

但就算我们采用了第1种方式，我们也必须用世界矩阵变换一下模型，让他们从模型空间变换到世界空间中——这导致在这种picking方式下，我们既需要变换模型，又要变换ray（除非把ray一直变到模型空间中，这也行）。但在一般的游戏中，我们会保留一个“模型－视图”矩阵——也就是世界矩阵和相机矩阵的归并，在这种情况下，采用第2种方式的代价比第1种要小——ray不需要任何变换。值得注意的一点是，如果采用第一种方式，并且使用了上面所描述的ray的第2种表达结构，对于m_direction的变换，需要采用相机逆矩阵的逆转置，这和变换polygon的法线是同一个道理，对于此问题迷惑的读者可以搜索法线变换相关主题。

总结

到目前位置，我们已经探讨了关于3D picking的主要理论方法。很多图形API（比如OpenGL）都提供了相关的方法来简化picking操作，可能picking的阶段有所差异，或者进行了某些优化，或者CVV定义不同，而原理大同小异。但一个统一的要求就是需要对流水线有一个细节层次上的认识，如此才能在不断变化的需求中找到合理的解决方案。