地铁系统 POJ1635 subway tree systems 判断树同构 DFS搜索子串
题目给出两个串,判断这两个串是否表示同一颗树。如果str1和str2表示同一颗树,那肯定“殊路同归”,即最终肯定能变换成同一种形式。所以,算法的基本思路:把str1和str2都转换成标准形式,然后判断是否相同。
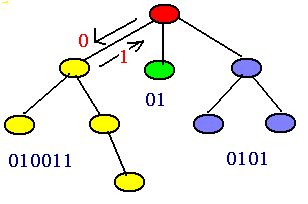
最终的“标准形式”是什么?先分析一下,这些串有什么特点。“万法归宗”,从根节点出发,最终还要回到根节点。对树的每条边,有去必有回,去为0,回为1。显然,遍历整个树会得到一个串,而这个串里面的o和1个数相等。由递归性可知,遍历子树得到的串,0和1也相等。也就是说,遍历的整个过程就是得到许多01相等的串。而题目中所给的串恰由这些子串构成。这样,如果对这些子串按字典顺序排序(也就是调用sort),原串就可以变为另外一种形式。而且,对任意一个原串都可以进行该过程。这就是我们要找的:标准形式。 如图所示:因为从根到子树要经过一条边,所以子串要去掉前导0和结尾的1。.
原串:0010011101001011
子串:00100111 01 001011
最后,在整理一下思路:首先对str1和str2分别提取子串,然后对str1的所有子串进行排序,对str2的所有子串也进行排序。最后,如果排序结果相同,则同构。
#include <iostream> #include <string> #include <vector> #include <algorithm> using namespace std; //***********************常量定义***************************** //*********************自定义数据结构************************* //********************题目描述中的变量************************ //**********************算法中的变量************************** string DFS( string tree ) { //只有前导0和结尾的1 //即已经到叶子节点,无子树,直接返回 if( tree == "01" ) return tree; //去掉前导0和结尾的1 int len = (int)tree.size(); string root = tree.substr( 1, len-2 ); //求树的子树 //也就是求串的子串,DFS递归调用 int cnt = 0; int start = 0; vector<string> sub; for( int i=0; i<len-2; i++ ) { cnt += ( root[i] == '0' ) ? 1 : -1; //当0和1的数目相等时,即找到一个子串 if( cnt == 0 ) { sub.push_back( DFS( root.substr( start, i-start+1 ) ) ); start = i+1; } } //加上前导0和结尾的1 string ans = "0"; //对串的子串进行排序 //因为排序是放在递归里, 所以最终对所有的子串都按字典顺序排序了 sort( sub.begin(), sub.end() ); int sz = (int)sub.size(); for( int j=0; j<sz; j++ ) { ans += sub[j]; } return ans + "1"; } //***********************算法实现***************************** //************************main函数**************************** int main() { //freopen( "in.txt", "r", stdin ); int caseNum; cin >> caseNum; while( caseNum-- ) { string a, b, ansA, ansB; cin >> a; a = "0" + a + "1"; ansA = DFS( a ); cin >> b; b = "0" + b + "1"; ansB = DFS( b ); if( ansA == ansB ) cout << "same" << endl; else cout << "different" << endl; } return 0; }