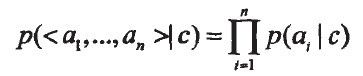朴素的贝叶斯分类器（Naive Bayesian Classifier）

贝叶斯理论是处理不确定性信息的重要工具。作为一种不确定性推理方法，它基于概率和统计理论，具有坚实的数学基础，贝叶斯网络在处理不确定信息的智能化系统中已经得到了广泛的应用，并且成功地用于医疗诊断、统计决策、专家系统等领域。这些成功的应用，充分说明了贝叶斯技术是一种强有力的不确定性推理方法。贝叶斯分类器分为两种：一种是朴素贝叶斯分类器，另一种贝叶斯网分类器。

朴素贝叶斯分类器是一种有监督的学习方法，其假定一个属性的值对给定类的影响而独立于其他属性值，此限制条件较强，现实中往往不能满足，但是朴素贝叶斯分类器取得了较大的成功，表现出高精度和高效率，具有最小的误分类率，耗时开销小的特征。贝叶斯网分类器是一种有向无环图模型，能够表示属性集间的因果依赖。通过提供图形化的方法来表示知识，以条件概率分布表表示属性依赖关系的强弱，将先验信息和样本知识有机结合起来；通过贝叶斯概率对某一事件未来可能发生的概率进行估计，克服了基于规则的系统所具有的许多概念和计算上的困难。其优点是具有很强的学习和推理能力，能够很好地利用先验知识，缺点是对发生频率较低的事件预测效果不好，且推理与学习过程是NP—Hard的。

分类有基于规则的分类(查询)和非规则分类(有指导学习)。贝叶斯分类是非规则分类，它通过训练集(已分类的例子集)训练而归纳出分类器(被预测变量是离散的称为分类，连续的称为回归)，并利用分类器对未分类的数据进行分类。贝叶斯分类器中有代表性的分类器有朴素贝叶斯分类器、贝叶斯网络分类器和树增强朴素贝叶斯分类模型TAN等。

贝叶斯分类具有如下特点：

(1)贝叶斯分类并不是把一个实例绝对指派给某一类，而是通过计算得出属于某一类的概率，具有最大概率的类是该实例所属的类。

(2)一般情况下在贝叶斯分类中的所有属性都直接或间接地发挥作用，即所有的属性都参与分类，而不是一个或几个属性决定分类。

(3)贝叶斯分类实例的属性可以是离散的、连续的，也可以是混合的。

假设A1,A2,...,An是数据集的n个特征(属性)，假设有m个类,C={C1.C2,...Cm}给定一个具体的实例工其属性为{xl,x2,...,Xn}，这里Xi是属性Ai的具体取值，该实例属于某一个类Ci的后验概率是P(X|Ci)，C(X)表示分类所得的类标签。贝叶斯分类器表示为：

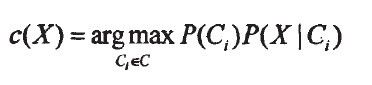
即预测实例X属于在属性给定条件下后验概率最大的类别时，预测的正确率最大。

朴素贝叶斯分类模型

但是公式上述的后验概率难以计算，因此朴素贝叶斯分类器引入了以下假设：在给定类别C的条件下，所有的属性Ai相互独立。即：

被称为“朴素贝叶斯假设“。

用贝叶斯网表达的朴素贝叶斯分类器如下图所示：

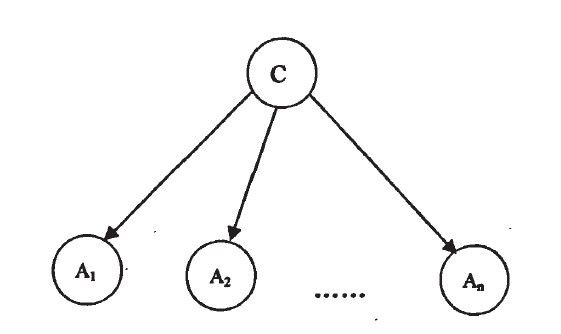
在朴素贝叶斯分类算法中，既可以独立的学习每个属性Ai在类别属性C下的条件概率P(Ai|C)，也可以独立学习每个属性Ai的概率，因该值为常数，可用归一化因子a来代替。然后，分类器应用贝叶斯公式计算特定实例数据在给定属性值下类别的后验概率：

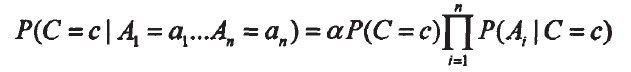
并预测该实例属于后验概率最大的类别。

朴素贝叶斯分类器的学习和分类

根据上述公式可知，最优分类C=Ci应该同时满足满足：

类别C的先验概率分布可以简单的从训练集数据中获得其最大似然估计，等于不同类别属性在数据集中出现的频度，计算复杂度为O(|D|)。

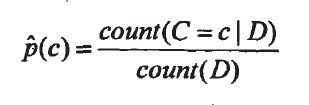
由于实例<al,...,an>的概率P(<al,...,an>)是一常数，在计算中仅进行归一化处理，因此，学习的过程主要是通过训练集估计属性的后验概率P(<al,...,an>|c)。根据朴素贝叶斯假设，应用贝叶斯公式展开:

右边的每一项均可以用下式估计：

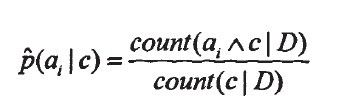
上式给出了最大似然度下的基于训练数据集的参数估计值，同样可在O(|D|)时间内计算。

朴素贝叶斯分类模型的优势是：

1)算法逻辑简单，易于实现；

2)分类过程中时间、空间开销小；

3)算法性能稳定，对于不同的数据特点其分类性能差别不大，即模型健壮性比较好。