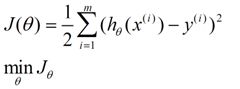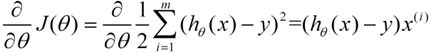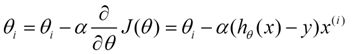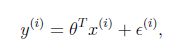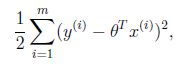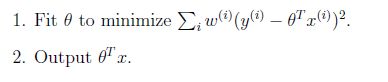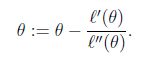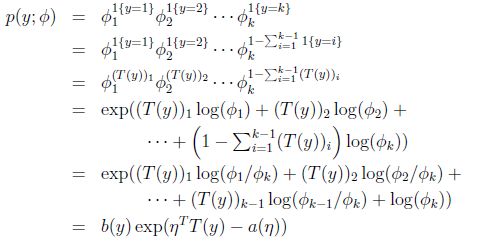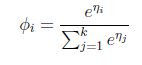线性回归和logistic回归

转自：http://www.cnblogs.com/jerrylead/archive/2011/03/05/1971867.html

红字处是个人的理解

1 摘要

      本报告是在学习斯坦福大学机器学习课程前四节加上配套的讲义后的总结与认识。前四节主要讲述了回归问题，回归属于有监督学习中的一种方法。该方法的核心思想是从连续型统计数据中得到数学模型，然后将该数学模型用于预测或者分类。该方法处理的数据可以是多维的。

     讲义最初介绍了一个基本问题，然后引出了线性回归的解决方法，然后针对误差问题做了概率解释。之后介绍了logistic回归。最后上升到理论层次，提出了一般回归。

2 问题引入

     这个例子来自http://www.cnblogs.com/LeftNotEasy/archive/2010/12/05/mathmatic_in_machine_learning_1_regression_and_gradient_descent.html

     假设有一个房屋销售的数据如下：

面积(m^2)	销售价钱（万元）
123	250
150	320
87	160
102	220
…	…

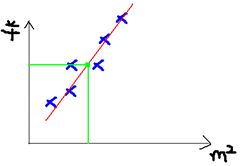
     这个表类似于北京5环左右的房屋价钱，我们可以做出一个图，x轴是房屋的面积。y轴是房屋的售价，如下：

     

     如果来了一个新的面积，假设在销售价钱的记录中没有的，我们怎么办呢？

     我们可以用一条曲线去尽量准的拟合这些数据，然后如果有新的输入过来，我们可以在将曲线上这个点对应的值返回。如果用一条直线去拟合，可能是下面的样子：

     

     绿色的点就是我们想要预测的点。

     首先给出一些概念和常用的符号。

     房屋销售记录表：训练集(training set)或者训练数据(training data), 是我们流程中的输入数据，一般称为x

     房屋销售价钱：输出数据，一般称为y

     拟合的函数（或者称为假设或者模型）：一般写做 y = h(x)

     训练数据的条目数(#training set),：一条训练数据是由一对输入数据和输出数据组成的输入数据的维度n (特征的个数，#features)

     这个例子的特征是两维的，结果是一维的。然而回归方法能够解决特征多维，结果是一维多离散值或一维连续值的问题。

3 学习过程

     下面是一个典型的机器学习的过程，首先给出一个输入数据，我们的算法会通过一系列的过程得到一个估计的函数，这个函数有能力对没有见过的新数据给出一个新的估计，也被称为构建一个模型。就如同上面的线性回归函数。

     

4 线性回归

     线性回归假设特征和结果满足线性关系。其实线性关系的表达能力非常强大，每个特征对结果的影响强弱可以由前面的参数体现，而且每个特征变量可以首先映射到一个函数，然后再参与线性计算。这样就可以表达特征与结果之间的非线性关系。

     我们用X1，X2..Xn 去描述feature里面的分量，比如x1=房间的面积，x2=房间的朝向，等等，我们可以做出一个估计函数：

     

     θ在这儿称为参数，在这的意思是调整feature中每个分量的影响力，就是到底是房屋的面积更重要还是房屋的地段更重要。为了如果我们令X0 = 1，就可以用向量的方式来表示了：

     

     我们程序也需要一个机制去评估我们θ是否比较好，所以说需要对我们做出的h函数进行评估，一般这个函数称为损失函数（loss function）或者错误函数(error function)，描述h函数不好的程度，在下面，我们称这个函数为J函数

     在这儿我们可以认为错误函数如下：

     

     这个错误估计函数是去对x(i)的估计值与真实值y(i)差的平方和作为错误估计函数，前面乘上的1/2是为了在求导的时候，这个系数就不见了。

     至于为何选择平方和作为错误估计函数，讲义后面从概率分布的角度讲解了该公式的来源。

     如何调整θ以使得J(θ)取得最小值有很多方法，其中有最小二乘法(min square)，是一种完全是数学描述的方法，和梯度下降法。

5 梯度下降法

     在选定线性回归模型后，只需要确定参数θ，就可以将模型用来预测。然而θ需要在J(θ)最小的情况下才能确定。因此问题归结为求极小值问题，使用梯度下降法。梯度下降法最大的问题是求得有可能是全局极小值，这与初始点的选取有关。

     梯度下降法是按下面的流程进行的：

     1）首先对θ赋值，这个值可以是随机的，也可以让θ是一个全零的向量。

     2）改变θ的值，使得J(θ)按梯度下降的方向进行减少。

     梯度方向由J(θ)对θ的偏导数确定，

由于求的是极小值，因此梯度方向是偏导数的反方向。结果为

          

     迭代更新的方式有两种，一种是批梯度下降，也就是对全部的训练数据求得误差后再对θ进行更新，另外一种是增量梯度下降，每扫描一步都要对θ进行更新。前一种方法能够不断收敛，后一种方法结果可能不断在收敛处徘徊。

     一般来说，梯度下降法收敛速度还是比较慢的。

     另一种直接计算结果的方法是最小二乘法。

6 最小二乘法

     将训练特征表示为X矩阵，结果表示成y向量，仍然是线性回归模型，误差函数不变。那么θ可以直接由下面公式得出

令J(θ) = 0得

     但此方法要求X是列满秩的，而且求矩阵的逆比较慢。

7 选用误差函数为平方和的概率解释

     假设根据特征的预测结果与实际结果有误差，那么预测结果和真实结果满足下式：

     一般来讲，误差满足平均值为0的高斯分布，也就是正态分布。那么x和y的条件概率也就是

     这样就估计了一条样本的结果概率，然而我们期待的是模型能够在全部样本上预测最准，也就是概率积最大。注意这里的概率积是概率密度函数积，连续函数的概率密度函数与离散值的概率函数不同。这个概率积成为最大似然估计。我们希望在最大似然估计得到最大值时确定θ。那么需要对最大似然估计公式求导，求导结果既是

          

     这就解释了为何误差函数要使用平方和。

     当然推导过程中也做了一些假定，但这个假定符合客观规律。

8 带权重的线性回归

     上面提到的线性回归的误差函数里系统都是1，没有权重。带权重的线性回归加入了权重信息。

     基本假设是

          

     其中假设符合公式

               

     其中x是要预测的特征，这样假设的道理是离x越近的样本权重越大，越远的影响越小。这个公式与高斯分布类似，但不一样，因为不是随机变量。

     此方法成为非参数学习算法，因为误差函数随着预测值的不同而不同，这样θ无法事先确定，预测一次需要临时计算，感觉类似KNN。

9 分类和logistic回归

     一般来说，回归不用在分类问题上，因为回归是连续型模型，而且受噪声影响比较大。如果非要应用进入，可以使用logistic回归。

     logistic回归本质上是线性回归，只是在特征到结果的映射中加入了一层函数映射，即先把特征线性求和，然后使用函数g(z)将最为假设函数来预测。g(z)可以将连续值映射到0和1上。

     logistic回归的假设函数如下，线性回归假设函数只是。

     logistic回归用来分类0/1问题，也就是预测结果属于0或者1的二值分类问题。这里假设了二值满足伯努利分布，也就是

     当然假设它满足泊松分布、指数分布等等也可以，只是比较复杂，后面会提到线性回归的一般形式。

     与第7节一样，仍然求的是最大似然估计，然后求导，得到迭代公式结果为

     

logistic在梯度下降的时候却取梯度的正方向，这是因为logistic求的是最大值，而上面的线性回归求的是Loss的最小值，所以去梯度的负方向。

     可以看到与线性回归类似，只是换成了，而实际上就是经过g(z)映射过来的。

10 牛顿法来解最大似然估计

     第7和第9节使用的解最大似然估计的方法都是求导迭代的方法，这里介绍了牛顿下降法，使结果能够快速的收敛。

Andrew举例很形象，

     当要求解时，如果f可导，那么可以通过迭代公式

     来迭代求解最小值。

     当应用于求解最大似然估计的最大值时，变成求解最大似然估计概率导数的问题。

目标函数是l(ϴ)

找到l’(ϴ) = 0的点

这个点就局部最优点，但是不能直接求出

设f(ϴ)= l’(ϴ)，也就是求f(ϴ)=0

取一点ϴ₀，则f(ϴ)的斜率l’’(ϴ₀) = l’(ϴ₀)/( ϴ_i- ϴ₀),所以ϴ_i = ϴ₀ - l’(ϴ₀)/ l’’(ϴ₀)

     那么迭代公式写作

     

     当θ是向量时，牛顿法可以使用下面式子表示

      

     其中是n×n的Hessian矩阵。

     牛顿法收敛速度虽然很快，但求Hessian矩阵的逆的时候比较耗费时间。

     当初始点X0靠近极小值X时，牛顿法的收敛速度是最快的。但是当X0远离极小值时，牛顿法可能不收敛，甚至连下降都保证不了。原因是迭代点Xk+1不一定是目标函数f在牛顿方向上的极小点。

11 一般线性模型

     之所以在logistic回归时使用

     

     的公式是由一套理论作支持的。

     这个理论便是一般线性模型。

     首先，如果一个概率分布可以表示成

     

     时，那么这个概率分布可以称作是指数分布。

     伯努利分布，高斯分布，泊松分布，贝塔分布，狄特里特分布都属于指数分布。

     在logistic回归时采用的是伯努利分布，伯努利分布的概率可以表示成

     

     其中

     

     得到

     

     这就解释了logistic回归时为了要用这个函数。

     一般线性模型的要点是

     1）  满足一个以为参数的指数分布，那么可以求得的表达式。

     2） 给定x，我们的目标是要确定，大多数情况下，那么我们实际上要确定的是，而。（在logistic回归中期望值是，因此h是；在线性回归中期望值是，而高斯分布中，因此线性回归中h=）。

     3） 

12 Softmax回归

     最后举了一个利用一般线性模型的例子。

     假设预测值y有k种可能，即y∈{1,2,…,k}

     比如k=3时，可以看作是要将一封未知邮件分为垃圾邮件、个人邮件还是工作邮件这三类。

     定义

     

     那么

     

     这样

     

     即式子左边可以有其他的概率表示，因此可以当作是k-1维的问题。

     为了表示多项式分布表述成指数分布，我们引入T(y)，它是一组k-1维的向量，这里的T(y)不是y，T(y)i表示T(y)的第i个分量。

     

     应用于一般线性模型，结果y必然是k中的一种。1{y=k}表示当y=k的时候，1{y=k}=1。那么p(y)可以表示为

     

     其实很好理解，就是当y是一个值m（m从1到k）的时候，p(y)=，然后形式化了一下。

     那么

     

     最后求得

     

     而y=i时

     

     求得期望值

     那么就建立了假设函数，最后就获得了最大似然估计

     对该公式可以使用梯度下降或者牛顿法迭代求解。

     解决了多值模型建立与预测问题。

 

 

学习总结

     该讲义组织结构清晰，思路独特，讲原因，也讲推导。可贵的是讲出了问题的基本解决思路和扩展思路，更重要的是讲出了为什么要使用相关方法以及问题根源。在看似具体的解题思路中能引出更为抽象的一般解题思路，理论化水平很高。

     该方法可以用在对数据多维分析和多值预测上，更适用于数据背后蕴含某种概率模型的情景。

几个问题

     一是采用迭代法的时候，步长怎么确定比较好

     而是最小二乘法的矩阵形式是否一般都可用