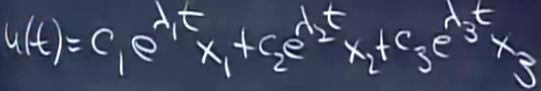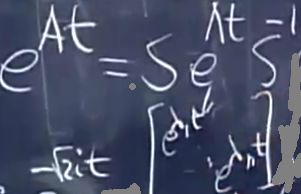线性代数导论33——第三阶段总结
本文是Gilbert Strang的线性代数导论课程笔记。课程地址: http://v.163.com/special/opencourse/daishu.html
第三十三课时:第三阶段总结复习
本讲梳理知识要点:1)特征值与特征向量Ax=λx;2)微分方程;3)对称矩阵A=A
T的特征值是实数,总存在足够的特征向量特征值使它可以对角化:A=
Q
ΛQT;4)正定矩阵是特征值均为正的对称矩阵;5)相似矩阵满足B=M
-1AM,A与B的特征值相同,它的关键在于,通过不同的基表示同样的变换动作,且B
k=M
-1A
kM,所以,虽然M改变了矩阵的特征向量,但不会改变特征值;6)奇异值分解SVD。
1)矩阵可对角化的本质即要有足够的特征向量可以线性无关;
2)投影矩阵的特征值为0和1;
3)正交矩阵的特征值的绝对值等于1,正交矩阵的作用就像旋转,不会改变向量的长度;
4)当矩阵满足:AAT=ATA 时,A的特征向量正交。对称阵,反对称阵,正交矩阵 是满足此条件的三类矩阵;
5)SVD:任意矩阵 A=UΣVT=(orthog)(diag)(orthog),V是ATA的特征向量矩阵,U是AAT的特征向量矩阵。具体做奇异值分解时,奇异值σ是对角矩阵Σ对角线上的元素,它的值等于(ATA)的特征值的正平方根,但值得注意的一点是:在求AAT的特征向量的时候,方向要由Avi=σiui来确定。
题1:解微分方程
求通解u(t)
求出特征向量和特征值,然后通过初始值确定c1,c2..常数。A的第一行和第三行线性相关,这是一个奇异矩阵,奇异矩阵的有一个特征值为0,同时,这是一个反对称矩阵,A=-A
T,特征值为纯虚数。此解既不发散也不收敛于0,而是稳定在某值,且具有周期性。指数矩阵形式如下:
题2:已知3×3的矩阵的特征向量和两个特征值
1)这个矩阵可以对角化吗?当c满足什么条件时,矩阵可对角化。
因为矩阵能否对角化只与是否有足够多的特征向量有关,因此c为任何值时矩阵都可以对角化。
2)当c为何值时,矩阵是对称的?
这三个特征向量正交,对称轴的特征值都是实数。所以当c为实数时矩阵对称。
3)当c为何值时,矩阵是正定的?
因为有一个特征值是等于0的,所以矩阵不可能是正定的。但如果c>=0,矩阵是半正定的。
4)矩阵可能是马尔科夫矩阵吗?
不可能,因为马尔科夫矩阵的特征值都小于等于1.
5)A/2可能是投影矩阵吗?
投影矩阵的特征值为0和1, P
2=P
, λ
2=λ
,所以当c=2或0时满足条件。
题3:对于如下情况,因为奇异值不等于0,所以这个矩阵肯定是2×2可逆矩阵。
如果Σ对右下角不是2是0,那么矩阵A是一个奇异矩阵。秩为1,那么零空间呢?0特征值对应的特征向量是v2,v2就在零空间里。从SVD可以看到四个基本子空间。
题4:A对称且正交
1)A的特征值是1或-1。因为对称阵的特征值是实数,正交矩阵的特征的绝对值是1。
2)A是非奇异矩阵;
3)(A+I)/2 是投影矩阵。验证P
2=P,且特征值为0和1.