Gradient And Karush-Kuhn-Tucker Conditions
转自:http://www.cnblogs.com/vivounicorn/archive/2011/12/29/2306060.html
作者讲得很详细,赞!
一、梯度是什么?
1、一个小例子
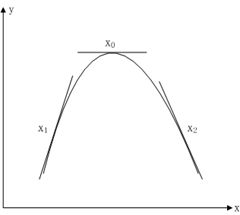
假设有单变量实值函数,其图形如下:
在自变量发生微小变化时,目标函数值的变化可以这么描述:
针对上图有以下三种情况:
(1)、点位置,此时,在 点做微小正向变化:,显然有,这说明在点往轴正向有可以使目标函数值增大点存在;
(2)、点位置,此时,在 点做微小负向变化:,显然有,这说明在点往轴负向有可以使目标函数值增大点存在;
(3)、点位置,此时,不管在 点做微小负向变化还是正向变化都有,这说明在点是一个最优解。
实际上,在一维情况下目标函数的梯度就是,它表明了目标函数值变化方向。
2、梯度与方向导数
(1)、方向导数
以二元函数:为例,设它在点的某个邻域内有定义,以点出发引射线,为上的且在邻域内的任意点,则方向导数的定义为:
其中表示和两点之间的欧氏距离:
从这个式子可以看到:方向导数与某个方向有联系、方向导数是个极限值、方向导数与偏导数似乎有联系。
实际上,如果在点可微,则:
其中和分别是两个维度上的方向角
这里需要注意的一个细节是:沿某个维度的方向导数存在时,其偏导数不一定存在,原因就是方向导数只要求半边极限存在(),而偏导数则要求双边都存在。
(2)、梯度
把方向导数变换一下形式:
函数在点的梯度就被定义为向量:
与射线同方向的单位向量被定义为:
于是方向导数变成了:
我的理解是:方向导数描述了由各个维度方向形成的合力方向上函数变化的程度,当这个合力方向与梯度向量的方向相同时,函数变化的最剧烈,我想这就是为什么在梯度上升算法或者梯度下降算法中选择梯度方向或者负梯度方向的原因吧。换句话说就是:函数在某点的梯度是这样一个向量,它的方向与取得最大方向导数的方向一致,而它的模为方向导数的最大值。
某个函数和它的等高线,图中标出了a点的梯度上升方向
3、多维无约束问题
将开篇的那个小例子扩展到多维的情况,目标函数值将会成为一个向量,向任意个维度方向做微小变动都将对目标函数值产生影响,假设有n个维度,可以用下面的式子描述:
令
(1)、当,此时,因此可以从点移动使得目标函数值增加;
(2)、当,此时,因此可以从点移动使得目标函数值减少;
(3)、当,梯度向量和正交(任一向量为0也视为正交),不管从点怎样移动都找不到使目标函数值发生变化的点,于是点就是目标函数的最优解。
由于可以是任意方向向量,只要点的梯度向量不为零,从点出发总可以找到一个变化方向使得目标函数值向我们希望的方向变化(比如就找梯度方向,此时能引起目标函数值最剧烈地变化),理论上当最优解出现时就一定有(实际上允许以某个误差结束),比如,对于梯度下降算法,当时迭代结束,此时的为最优解(可能是全局最优解也可能是局部最优解):
二、拉格朗日乘数法和KKT条件
从现在开始,我假设目标函数和约束在某点可微,用符号代替符号。
1、等式约束
 在约束条件的作用下,与点(它是个向量)可移动方向相关的向量就不像无约束问题那样随便往哪个方向都能移动了,此时只能沿着约束曲线移动,例如,在、处,和不正交,说明还有使目标函数值更小的等高线存在,所以点还有移动的余地,当移动到位置时和正交,得到最优解。那么在最优解处和约束有什么关系呢?因为此时,,显然此时有(其中是常数),也就是说约束的梯度向量与目标函数的梯度向量在最优解处一定平行。
在约束条件的作用下,与点(它是个向量)可移动方向相关的向量就不像无约束问题那样随便往哪个方向都能移动了,此时只能沿着约束曲线移动,例如,在、处,和不正交,说明还有使目标函数值更小的等高线存在,所以点还有移动的余地,当移动到位置时和正交,得到最优解。那么在最优解处和约束有什么关系呢?因为此时,,显然此时有(其中是常数),也就是说约束的梯度向量与目标函数的梯度向量在最优解处一定平行。
想到求解此类优化问题时最常用的方法——拉格朗日乘数法,先要构造拉格朗日函数:
其中,是常数
为什么求解拉格朗日函数得到的最优解就是原问题的最优解呢?
假设、为的最优解,那么就需要满足:
第一个式子印证了约束的梯度向量与目标函数的梯度向量在最优解处一定平行,第二个式子就是等式约束本身。
于是:
2、不等式约束
实际情况中,约束条件可能是等式约束也可能是不等式约束或者同时包含这两种约束,下面描述为更一般地情况:
依然使用拉格朗日乘数法,构造拉格朗日函数:
其中且
在这里不得不说一下Fritz John 定理了,整个证明就不写了(用局部极小必要条件定理、Gordan 引理可以证明)。
定理1:
依然假设为上述问题的极小值点,问题中涉及到的各个函数一阶偏导都存在,则存在不全为零的使得下组条件成立:
这个定理第一项的形式类似于条件极值必要条件的形式,如果则有效约束会出现正线性相关,由Gordan 引理知道此时将存在可行方向,就是将不是原问题的极值点,因此令则线性无关则。
这个条件又叫互不松弛条件(Complementary Slackness),SVM里的支持向量就是从这个条件得来的。
由Fritz John 定理可知线性无关则,让每一个拉格朗日乘子除以,即,得到下面这组原问题在点处取得极小值一阶必要条件。
定理2:
假设为上述问题的极小值点,问题中涉及到的各个函数一阶偏导都存在,有效约束线性无关,则下组条件成立:
这组条件就是Karush-Kuhn-Tucker条件,满足KKT条件的点就是KKT点,需要注意的是KKT条件是必要条件(当然在某些情况下会升级为充要条件,比如凸优化问题)。
由此也可以想到求解SVM最大分类间隔器时,不管是解决原问题还是解决对偶问题,不管是用SMO方法或其它方法,优化的过程就是找到并优化违反KKT条件的最合适的乘子。
KKT条件与对偶理论有密切的关系,依然是解决下面这个问题:
构造拉格朗日函数:
其中且,它们都是拉格朗日乘子
令,原问题可以表示为下面这个形式:
这个式子比较容易理解,当违反原问题约束条件时有:
于是原问题等价为下面这个问题:
它的最优解记为
令,则有以下形式:
它的最优解记为
上面这两个形式很像,区别只在于和的顺序,实际上和互为对偶问题。因为,打个不太恰当的比喻,这就像瘦死的骆驼比马大,具体的证明就不写了,所以,这个就是弱对偶性,此时存在对偶间隙,它被定义为:。
有弱对偶性就有强对偶性,它指的是在某些条件下有,比如在以下条件下满足强对偶性:
目标函数和所有不等式约束函数是凸函数,等式约束函数是仿射函数(形如),且所有不等式约束都是严格的约束(大于或小于)。
KKT条件和强对偶性的关系是:
KKT条件是强对偶性成立的必要条件,特别的,当原问题是凸优化问题时,KKT条件就是充要条件,强对偶性存在时KKT点既是原问题的解也是对偶问题的解,这个时候对偶间隙为0。
关于对偶问题可以参考pluskid写得非常好的一篇文章:http://blog.pluskid.org/?p=702
三、总结
梯度是一个基础而重要的概念,函数在某点的梯度是这样一个向量,它的方向与取得最大方向导数的方向一致,而它的模为方向导数的最大值,梯度下降算法正是依据这一原理,还有在求解极大似然问题时也可以用梯度上升的算法进行参数估计;对于约束最优化问题可以使用拉格朗日乘数法解决——如:构造拉格朗日函数,求出KKT条件;当原问题不太好解决的时候可以利用拉格朗日乘数法得到其对偶问题,满足强对偶性条件时它们的解会是一致的,SVM问题的解决把这一点用的淋漓尽致,同时也为我们提供了一种判断算法收敛情况的方法——监视可行间隙。