《数据结构复习笔记》--堆和堆排序

把堆的相关知识在复习一下。加深理解

堆排序与快速排序，归并排序一样都是时间复杂度为O(N*logN)的几种常见排序方法。学习堆排序前， 先来了解一下二叉堆。

二叉堆的定义

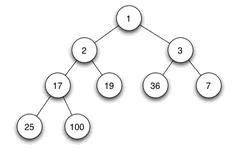
二叉堆是完全二叉树或者是近似完全二叉树。

二叉堆满足二个特性：

1．父结点的键值总是大于或等于（小于或等于）任何一个子节点的键值。

2．每个结点的左子树和右子树都是一个二叉堆（都是最大堆或最小堆）。

当父结点的键值总是大于或等于任何一个子节点的键值时为最大堆。当父结点的键值总是小于或等于任何一个子节点的键值时为最小堆。下图展示一个最小堆：

由于其它几种堆（二项式堆，斐波纳契堆等）用的较少，一般将二叉堆就简称为堆。

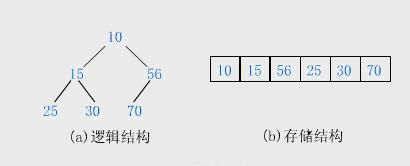
堆的存储

一般都用数组来表示堆，i结点的父结点下标就为(i – 1) / 2。它的左右子结点下标分别为2 * i + 1和2 * i + 2。如第0个结点左右子结点下标分别为1和2。

创建堆：

typedef struct HeapStruct *MaxHeap;//创建最大堆
struct HeapStruct
{
    ElementType *Elements; /* 存储堆元素的数组 */
    int Size; /* 堆的当前元素个数 */
    int Capacity; /* 堆的最大容量 */
};
MaxHeap Create( int MaxSize )
{
    /* 创建容量为MaxSize的空的最大堆 */
    MaxHeap H = malloc( sizeof( struct HeapStruct ) );
    H->Elements = malloc( (MaxSize+1) * sizeof(ElementType));
    H->Size = 0;
    H->Capacity = MaxSize;
    H->Elements[0] = MaxData;/*把MaxData换成小于堆中所有元素的MinData，同样适用于创建最小堆*/
    /* 定义“哨兵”为大于堆中所有可能元素的值，便于以后更快操作 */
    return H;
}

堆的操作——插入删除

<span style="font-size:12px;">void Insert( MaxHeap H, ElementType item )//算法：将新增结点插入到从其父结点到根结点的有序序列中,比交换数据要快
{
    /* 将元素item 插入最大堆H，其中H->Elements[0]已经定义为哨兵 */
    int i;
    if ( IsFull(H) )
    {
        printf("最大堆已满");
        return;
    }
    i = ++H->Size; /* i指向插入后堆中的最后一个元素的位置 */
    for ( ; H->Elements[i/2] < item; i/=2 )
        H->Elements[i] = H->Elements[i/2]; /* 向下过滤结点 */
    H->Elements[i] = item; /* 将item 插入 */
}

删除
ElementType DeleteMax( MaxHeap H )//最大堆的删除
{
    /* 从最大堆H中取出键值为最大的元素，并删除一个结点 */
    int Parent, Child;
    ElementType MaxItem, temp;
    if ( IsEmpty(H) )
    {
        printf("最大堆已为空");
        return;
    }
    MaxItem = H->Elements[1]; /* 取出根结点最大值 */
    /* 用最大堆中最后一个元素从根结点开始向上过滤下层结点 */
    temp = H->Elements[H->Size--];
    for( Parent=1; Parent*2<=H->Size; Parent=Child )
    {
        Child = Parent * 2;
        if( (Child!= H->Size) &&
                (H->Elements[Child] < H->Elements[Child+1]) )
            Child++; /* Child指向左右子结点的较大者 */
        if( temp >= H->Elements[Child] ) break;
        else /* 移动temp元素到下一层 */
            H->Elements[Parent] = H->Elements[Child];
    }
    H->Elements[Parent] = temp;
    return MaxItem;
}</span>

图解：

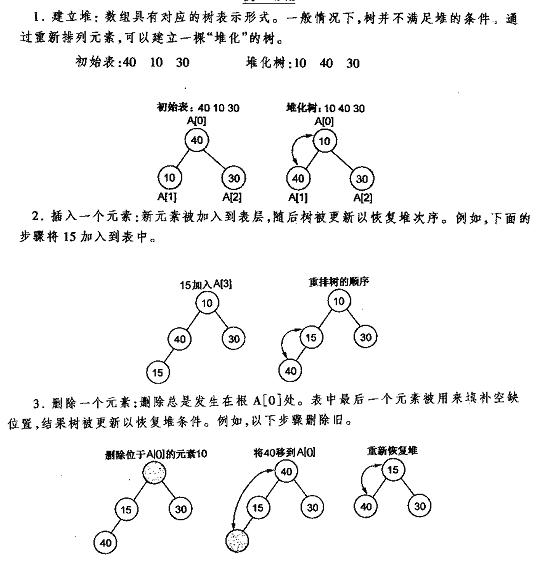
至此，可以得出最大堆的建立：
方法1：通过插入操作，将N个元素一个个相继插入到一个初始为空的堆中去，其时间代价最大为O(N logN)。
建立最大堆：将已经存在的N个元素按最大堆的要求存放在一个一维数组中。
方法2：在线性时间复杂度下建立最大堆。
（1）将N个元素按输入顺序存入，先满足完全二叉树的结构特性。
（2）调整各结点位置，以满足最大堆的有序特性。
 

堆排序

这里直接引用维基百科：比自己表达更全面。

堆排序算法的演示。首先，将元素进行重排，以符合堆的条件。图中排序过程之前简单的绘出了堆树的结构。

首先可以看到堆建好之后堆中第0个数据是堆中最小的数据。取出这个数据再执行下堆的删除操作。这样堆中第0个数据又是堆中最小的数据，重复上述步骤直至堆中只有一个数据时就直接取出这个数据。

由于堆也是用数组模拟的，故堆化数组后，第一次将A[0]与A[n - 1]交换，再对A[0…n-2]重新恢复堆。第二次将A[0]与A[n – 2]交换，再对A[0…n - 3]重新恢复堆，重复这样的操作直到A[0]与A[1]交换。由于每次都是将最小的数据并入到后面的有序区间，故操作完成后整个数组就有序了，有点类似选择排序。

#include <iostream>
using namespace std;
/*
	#堆排序#%
          #数组实现#%
*/
//#筛选算法#%
void sift(int d[], int ind, int len)
{
	//#置i为要筛选的节点#%
	int i = ind;
 
	//#c中保存i节点的左孩子#%
	int c = i * 2 + 1; //#+1的目的就是为了解决节点从0开始而他的左孩子一直为0的问题#%
 
	while(c < len)//#未筛选到叶子节点#%
	{
		//#如果要筛选的节点既有左孩子又有右孩子并且左孩子值小于右孩子#%
		//#从二者中选出较大的并记录#%
		if(c + 1 < len && d[c] < d[c + 1])
			c++;
		//#如果要筛选的节点中的值大于左右孩子的较大者则退出#%
		if(d[i] > d[c]) break;
		else
		{
			//#交换#%
			int t = d[c];
			d[c] = d[i];
			d[i] = t;
			//
			//#重置要筛选的节点和要筛选的左孩子#%
			i = c;
			c = 2 * i + 1;
		}
	}
 
	return;
}
 
void heap_sort(int d[], int n)
{
	//#初始化建堆, i从最后一个非叶子节点开始#%
	for(int i = (n - 2) / 2; i >= 0; i--)
		sift(d, i, n);
 
	for(int j = 0; j < n; j++)
	{
                //#交换#%
		int t = d[0];
		d[0] = d[n - j - 1];
		d[n - j - 1] = t;
 
		//#筛选编号为0 #%
		sift(d, 0, n - j - 1);
 
	}
}
 
int main()
{
	int a[] = {3, 5, 3, 6, 4, 7, 5, 7, 4}; //#QQ#%
 
	heap_sort(a, sizeof(a) / sizeof(*a));
 
	for(int i = 0; i < sizeof(a) / sizeof(*a); i++)
	{
		cout << a[i] << ' ';
	}
	cout << endl;
    return 0;
}

最坏情况下，时间复杂度：

，另外，注意，堆排序是一种不稳定的排序。