牛客堂刷题之KMP

题目：

给定两个字符串str和match，长度分别为N和M。实现一个算法，如果字符串str中含有字串match，
则返回match在str中的开始位置，不含有则返回-1。
【举例】
str=“acbc”，match=“bc”。返回2。
str=“acbc”，match=“bcc”。返回-1。
【要求】
如果match的长度大于str长度(M>N)，str必然不会含有match，可直接返回-1。
但如果N>=M，要求算法复杂度O(N)。

思路：

按照一般的思路，依次匹配不上，就要全部改造重来，势必会造成复杂度的上升。

KMP算法是：提前算好了next数组，然后按照next数组中的一些规律来减少我们匹配的复杂度

next数组表示的是当前元素 i 以前的最长前缀和最长后缀，

match串： 1  2  3 1  2 b

next数组：-1 0  0  0 1 2

1位置的时候，开始默认设置为-1

2位置的时候，以前的位置只有一个1，所以是0

3位置的时候，以前的是 1 2，所以还是0

1位置的时候，以前的是1 2 3，所以还是0
2位置的时候，以前是1 2 3 1，所以前缀是1，后缀是1，所以最长子串的长度是1
b位置，以前是1 2 3 1 2，所以最前缀是1 2，最后缀是1 2，两者相等，所以长度为2

类似的还有

match：     a a a a a b
next数组：-1 0 1 2 3 4 

我们先假设已经得到了next数组，先来看看如何匹配

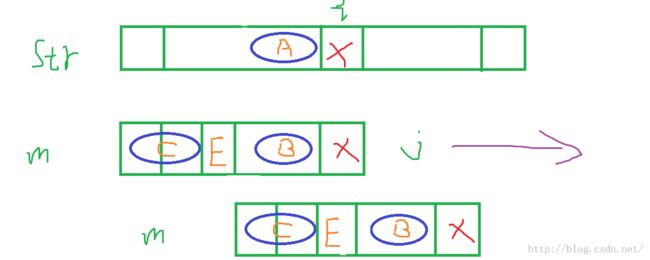
如图，假设str串和match串匹配到 i 和 j 处无法继续匹配，那么我们利用已经计算出的next数组

可以获取match串 j 位置的最长前缀 C和最长后缀B，A是和B相等的原串的一部分，显然C=A=B

所以下一次比较的时候可以直接比较元素E与str[i]，也就是match串向右移动。

比如说原串是1 2 3 1 2 1 2 3 4 6 7，匹配串是1 2 3 1 2 b，next数组是 -1 0  0  0 1 2

首先匹配是

1 2 3 1 2 1 2 3  4 6 7

1 2 3 1 2 b

当比较到1和b的位置时，无法继续匹配

此时next[b]的值是2，那么 右移后的结果就是

1 2 3 1 2 1 2 3  4 6 7

          1 2 3 1 2 b

此时再继续比较即可。

刚才图中我们省略了一部分，有一部分不用比较可以直接略去

如图所示

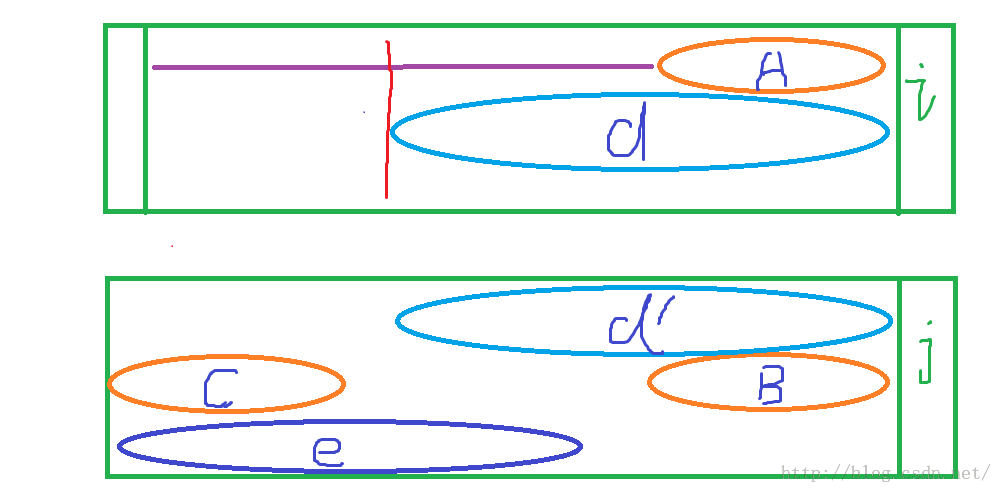
紫色横线这一部分可以直接省去，那么为什么可以省去呢？

我们先假设在紫色横线内找到了和match全部匹配的，假设是d和e全部匹配。

又因为str和match是匹配到最后一个才不相等，那么d和d‘也是相等的，所以d’和e就是相等的

那么d‘作为 j 位置的最后缀，e为j位置的最前缀，很明显a不等于e，d’不等于B，所以就与next计算出的最长前后缀产生矛盾，所以就不用比较这一部分的值

匹配完了，我们再继续看如何得出next数组

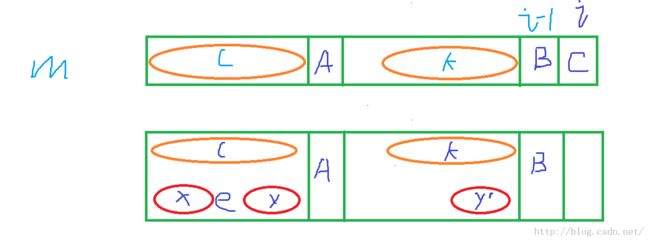
如图，我们要计算i位置的next值，假设已经比较到了A和B，L和K是已经全部相等的，

如果A和B相等，那么i位置的next值等于 i-1位置处的next值加1

如果A和B不相等，由于A的最长前缀 x 和后缀 y 我们已经计算出，显然y‘和y是相等的（都是l和k的末尾处）

所以我们只需要比较e和B是否相等即可。

代码：

package com.cowcode_fourth;

public class KmpTest {

	public static void main(String[] args) {
		 
		String str = "1231234";
		String ma = "1234121ab";
	 
		System.out.println(getIndexOf(str,ma));
	}
 
	
	 public static int getIndexOf(String s, String m) { 
	        if (s == null || m == null || m.length() < 1 || s.length() < m.length()) { 
	        return -1; 
	        } 
	        char[] ss = s.toCharArray(); 
	        char[] ms = m.toCharArray(); 
	        int si = 0; 
	        int mi = 0; 
	        int[] next = getNextArray(ms); 
	        while (si < ss.length && mi < ms.length) { 
	        if (ss[si] == ms[mi]) { 
	            si++;   //相等都加1
	            mi++; 
	        } else if (next[mi] == -1) { 
	            si++; 
	        } else { 
	            mi = next[mi]; //可以看做是向右滑动的过程
	        } 
	        } 
	        return mi == ms.length ? si - mi : -1; //如果找到，那么match串也就走完，直接和长度比较
	    } 


	    public static int[] getNextArray(char[] ms) { 
	        if (ms.length == 1) { 
	            return new int[] { -1 }; 
	        } 
	        int[] next = new int[ms.length]; 
	        next[0] = -1; 
	        next[1] = 0; 
	        int pos = 2; //要算的next元素的值
	        int cn = 0;  //可以看做是进位，相等了就向前进一位
	        while (pos < next.length) { 
	            if (ms[pos - 1] == ms[cn]) { 
	                next[pos++] = ++cn; 
	            } else if (cn > 0) { 
	                cn = next[cn];  //用cn的最长前缀值和其比较
	            } else { 
	                next[pos++] = 0; 
	            } 
	        } 
	        return next; 
	    }

}

复杂度：

匹配过程中，match不断向右移动，str匹配的位置时不退回的，所以最坏情况下，match向右滑动n个单位，所以时间复杂度为O(n)

计算next数组过程中，我们关注pos和pos-cn两个变量和求解next数组的代码

pos最小是0，最大是m，cn不可能大于m，所以有

                                           pos(0~~m)           pos-cn(0~~~m)

第一个循环分支：              增加                           不变

第二个循环分支：              不变                            增加

第三个循环分支：              增加                             增加

因为pos+pos-cn<=2m，所以循环总次数不可能大于2m，所以时间复杂度为O(m)

所以总体的复杂度是O(m)+O(n)

又因为KMP发生的条件是m<n，所以时间复杂度是O(n)