USACO 3.3.3 Packing Rectangles (packrec)(转)
报告:http://starforever.blog.hexun.com/2097115_d.html
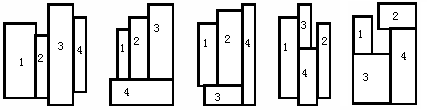
因为只有4个方块,所以枚举每个方块的选择顺序和放置方向(横放还是纵放),放置方式只有题目给出的6种基本模式,分别算出不同模式下最小的面积,更新最优解。
第4、5个在本质上其实是一样。如图,不同模式对应的最小面积如下:
设w1,w2,w3,w4表示4个方块的横长,h1,h2,h3,h4表示4个方块的纵长。w,h表示最小。
1:w=w1+w2+w3+w4;h=max(h1,h2,h3,h4)
2:w=max(w1+w2+w3,w4);h=max(h1,h2,h3)+h4
3:w=max(w1+w2,w3)+w4;h=max(h1+h3,h2+h3,h4)
4:w=w1+w2+max(w3,w4);h=max(h1,h3+h4,h2)
5:h=max(h1+h3,h2+h4)
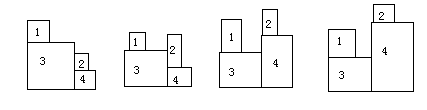
对于w,我们细分为如下四种形式:
(1):h3>=h2+h4;w=max(w1,w3+w2,w3+w4)
(2):h3>h4 and h3<h2+h4;w=max(w1+w2,w2+w3,w3+w4)
(3):h4>h3 and h4<h1+h3;w=max(w1+w2,w1+w4,w3+w4)
(4):h4>=h1+h3;w=max(w2,w1+w4,w3+w4)
*:h3=h4(图中没画);w=max(w1+w2,w3+w4)
用一个数组记录最优解,最后排序输出即可。