数据结构全攻略--线性结构不攻自破之栈和队列

      上篇博客讨论了线性结构的两种基本的结构顺序表和链表，它们两者各有优缺点。总之吧，当我们要存储容量不固定的数据结构并且要对数据进行多次插入和删除操作时要多考虑使用链表结构，当只涉及对存储的数据进行只存或只读操作时应优先选用顺序表结构。

继续讨论线性结构--栈和队列

 

一、线性结构

 

 1、栈

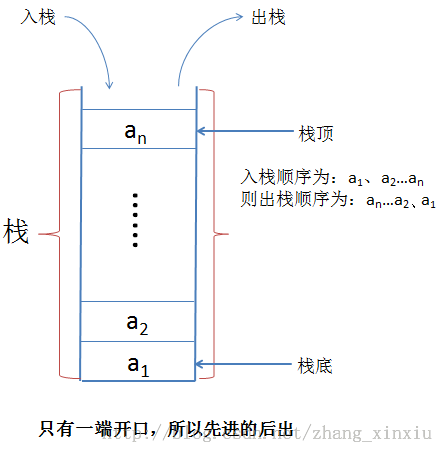
      栈是一种特殊的线性表。它的结构非常类似于日常生活中的瓶子，只有一端开口，而插入和删除的操作只能在瓶子的瓶口处进行，这种一端开口是它的特殊性。这种特殊性也决定了栈中的数据操作顺序是先入后出的，也就是说先进入栈中的数据，最后才能出去。

 

 

 
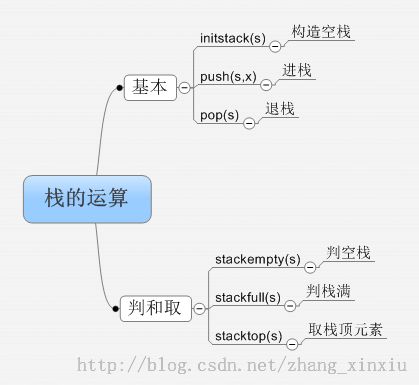
    栈的基本运算：

                  

      Note：栈是一种先进后出的线性表，但是并不意味着不会出现先进先出的情况。如：当1、2、3、4顺次入栈时，出栈的顺序也可能是1、2、3、4，这种情况发生条件是每个数入栈后出栈，然后下一个数入栈。即：1入栈后出栈，然后是2入栈后出栈，其次是3入栈后出栈，最后是4入栈后出栈，这样顺序就变成了1、2、3、4。
      由于栈也是线性表，因此线性表的存储结构对栈也适用，通常栈有顺序栈和链栈两种存储结构。

  1.1 顺序栈

 

      在顺序栈中数据是按照顺序进行存储的。需要我们了解的是顺序栈中有上溢和下溢的概念。
      上溢：栈顶指针指出栈的外面。我们把顺序栈看做一个盒子，那么当我们把数据放到这个栈中超过盒子的顶部时就放不下了，这时指针指向了栈的外面，这种现象我们称为上溢。
    下溢：从空栈中取数据。当栈中没有数据时，我们再去取数据，看看没数据，把盒子拎起来看看盒底，还是没有，这就是下溢。
顺序栈的类型定义为：

#define stacksize 100
　typedef char datatype;
　typedef struct{
　 datatype data[stacksize];
　 int top;
　}seqstack;

    1.1.1 顺序栈的基本运算

    (1) 置空栈

Void initstack(seqstack *s)
　　{
　　 s->top=-1;
　　}

    (2)判栈空

int stackempty(seqstack *s)
　　{
　　 return s->top==-1;
　　}

    (3)判栈满
　　

int stackfull(seqstack *s)
　　{
　　 return s->top==stacksize-1;
　　} 

    (4)进栈

Void push(seqstack *s,datatype x)
　　{
　　 if(stackfull(s))
　　  error(“stack overflow”);
　　 s->data[++s->top]=x;
　　}

     (5)退栈

Datatype pop(seqstack *s)
　　{
　　 if(stackempty(s))
　　  error(“stack underflow”);
　　 return S->data[s->top--];
　　}

     (6)取栈顶元素
　　

Dtatatype stacktop(seqstack *s)
　　{
　　 if(stackempty(s))
　　  error(“stack underflow”);
　　 return S->data[s->top];
　　}

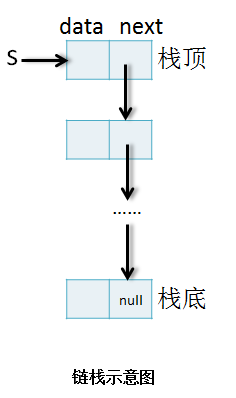
  1.2 链栈

      若是栈中元素的数目变化范围较大或不清楚栈元素的数目，就应该考虑使用链式存储结构。人们将用链式存储结构表示的栈称作"链栈"。链栈通常用一个无头结点的单链表表示。如图所示：

       和顺序栈不同，它没有固定的结构，也不会出现数据的上溢，它就像是一条一头固定的链子，可以在活动的一头自由地增加链环（结点）而不会溢出。

 

    1.2.1 基本运算

 

    (1) 建栈

Void initstack(linkstack *s)
{
　　s->top=NULL;
}

     (2)判栈空

Int stackempty (linkstack *s)
{
　 return s->top==NULL;
}

      (3) 进栈

Void push(linkstack *s,datatype x)
{
　　 stacknode *p=(stacknode *)malloc(sizeof(stacknode));
　　 p->data=x;
　　 p->next=s->top;
　　 s->top=p;
}

      (4) 退栈

Datatype pop(linksatck *s)
 { 　　 
    datatype x; 　　 
    stacknode *p=s->top; 

　　 if(stackempty(s)) 　　 
        error(“stack underflow”); 

　　 x=p->data; 　　 
    s->top=p->next; 　
　 
    free(p); 　　 
    return x; 
}

     (5) 取栈顶元素

Datatype stacktop(linkstack *s)
{
　　 if(stackempty(s))
　　   error(“stack is empty”);
　　 return s->top->data;
}

2、队列

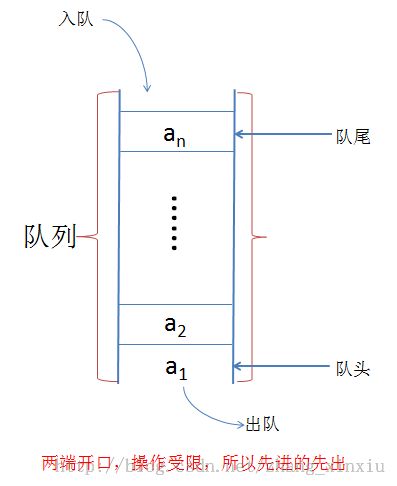
           队列也是一种运算受限的线性表，它的运算限制与栈不同，是两头都有限制。队列就如我们生活中常见的管道，两端开口。但又和我们常见的管道不同的是，它的插入操作只能在队列的队尾（rear）进行（只进不出），而删除只能在表的队头（Front）进行（只出不进），所以队列的操作原则是先进先出，所以队列又称作FIFO表（First In First Out）。

 

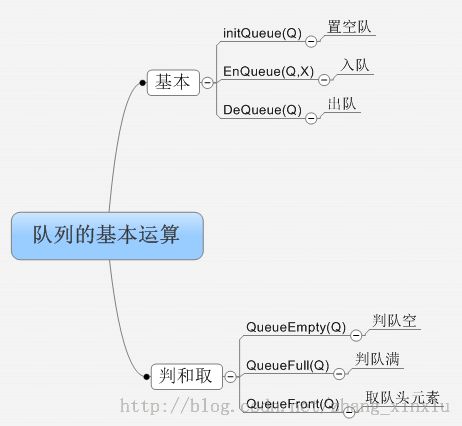
       队列的基本运算：

               

 

           队列也是一种线性结构，所以队列也有顺序存储和链式存储两种存储结构，前者称顺序队列，后者为链队。

 

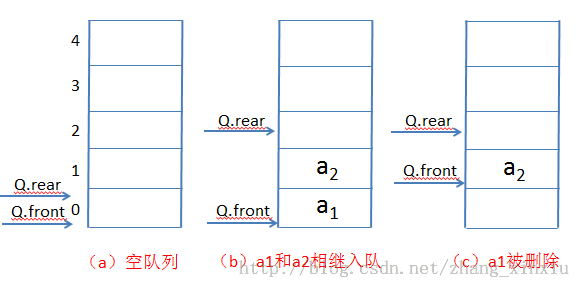
  2.1 顺序队列

 

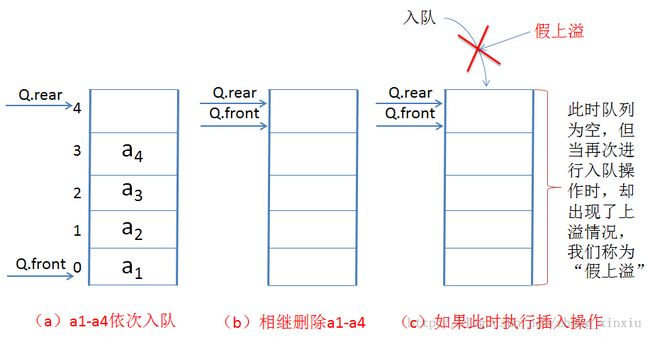
          与顺序栈类似，顺序队列也有上溢和下溢的情况，它们产生的原因和顺序栈类似，这里就不在细说。由于队列操作的特殊性（指针移动，元素不同）又出现了假上溢的情况。

 

           Note：在现实生活中我们随处可见排队的情况，当队列中的人离开队列后，后面的人会上来补上，当新来人排队时是在队列中的尾部进行排列的。我们现在说的队列和生活中的排队最大的区别在于前者是指针在移动，后者是元素在移动。
       Note：在队列中每插入一个元素，队列的队尾指针会向后移动一个位置；类似的在队列中每删除一个元素，队头的指针都会向接近队尾的方向移动一个位置。

 

 
     2.1.1 何为假上溢

 

          上图中的（c）操作，如果我们继续向队列中插入数据，尾指针就要跑到向量空间外面去了，尽管这时整个向量空间是空的，队列也是空的，却产生了“上溢”现象，这就是假上溢。

   2.1.2 队列的基本运算

       (1) 构造空队列

Void initqueue(cirqueue *q)
{
　　 q->front=q->rear=0;
　　 q->count=0;
}

      (2) 判队空

Int queueempty(cirqueue *q)
{
　　 return q->count==0;
}

      (3) 判队满

Int queuefull(cirqueue *q)
{
　　 return q->count==queuesize;
}

      (4) 入队

Void enqueue(cirqueue *q ,datatype x)
{
　　 if(queuefull(q))
　　   error(“queue overfolw”);
　　 q->count++;
　　 q->data[q->rear]=x;
　　 q->rear=(q->rear+1)%queuesize;
}

     (5) 出队

Datatype dequeue(cirqueue *q)
{
　　 datatype temp;
　　 if(queueempty(q))
　　  error(“queue underflow”);
　　 temp=q->data[q->front];
　　 q->count--;
　　 q->front=(q->front+1)%queuesize;
　　 return temp;
}

     (6) 取队头元素

Datatype queuefront(cirqueue *q)
{
　　 if(queueempty(q))
　　  error(“queue is empty”);
　　 return q->data[q->front];
}

 

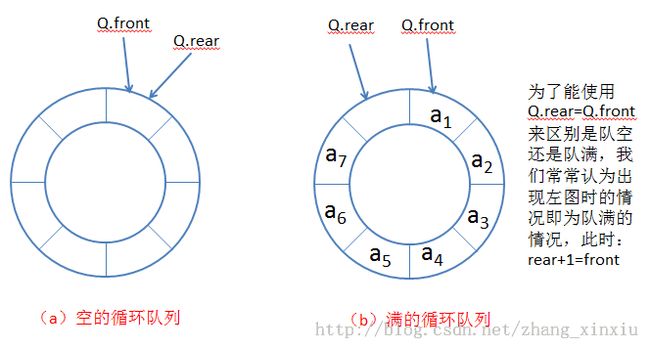
 2.2 循环队列

        为了克服线性队列造成的空间浪费，我们引入循环向量的概念，它就好像是把向量空间弯起来，形成一个头尾相接的环形，这样当队列的头尾指针移动到队列的尾部时，再进行入队的操作，就使指针指向队列的队头，也就是从头开始。这时的队列就称循环队列。
      通常我们所使用的大都是循环队列。但由于循环的原因，我们就不能当头尾指针重叠在一起来判断队列为空还是满的情况，为了避免这种情况，我们又引入了边界条件的概念。

 

解决方法有：
　     ① 另设一个布尔变量以区别队列的空和满；
　     ② 少用一个元素，当入队时，先测试入队后尾指针是不是会等于头指针，如果相等就算队已满，不许入队；
         ③ 使用一个记数器记录元素总数。

     2.2.1 循环队列的基本运算

       (1) 建空队

Void initqueue(linkqueue *q)
{
　　 q->front=q->rear=NULL;
}

         (2) 判队空

Int queueempty(linkqueue *q)
{
　　 return q->front==NULL&&q->rear==NULL;
}

          (3) 入队

Void enqueue(linkqueue *q,datatype x) { 　　 
     queuenode *p=(queuenode *)malloc(sizeof(queuenode)); 　　 
     p->data=x; 　　 
     p->next=NULL; 

　　 if(queueempty(q)) 　　 
        q-front=q->rear=p; 　　 
     else
      { 　　 
        q->rear->next=p; 　　 
        q->rear=p; 　　 
     } 
}

      (4) 出队

Datatype dequeue(linkqueue *q)
{
　　 datatype x;
　　 queuenode *p;
　　 if(queueempty(q))
　　   error(“queue is underflow”);

　   p=q->front;
　　 x=p->data;
　　 q->front=p->next;


　　 if(q->rear==p) 
       q->rear=NULL;


　　 free(p);
　　 return x;
}

      (5) 取队头元素
　　

Datatype queuefront(linkqueue *q)
{
　　 if(queueempty(q))
　　   error(“queue is empty”);

　　 return q->front->data;
}

 

3、结语

 

         至此，从头到尾的把数据结构的线性结构复习了一遍，相信经过上面的复习，对线性结构又有了更深入的了解。这部分的知识很重要，但是在软考中考的知识点却不深，需要我们掌握几种基本的线性结构的性质，并能熟练利用几种性质进行相关的数学运算。复习了基本知识点，接下来就应该进入实战阶段了。

      Suggest：在做题时，不要做完就算了，最好把做的题用到的知识点整理到笔记本上（不论是出错的还是正确的，当然错误的更要加强练习），然后在考试前经常翻看。

接下来将会进入非线性结构部分