第十二周项目四 利用遍历思想求解图问题

/*
* Copyright (c) 2015, 烟台大学计算机与控制工程学院
* All rights reserved.
* 文件名称： main.cpp,graph.h,graph.cpp
* 作者：巩凯强
* 完成日期：2015年11月23日
* 版本号：codeblocks
*
* 问题描述:  假设图G采用邻接表存储，分别设计实现以下要求的算法，要求用区别于示例中的图进行多次测试，通过观察输出值，掌握相关问题的处理方法
* 输入描述： 无
* 程序输出： 见运行结果
*/
#ifndef GRAPH_H_INCLUDED
#define GRAPH_H_INCLUDED
#include <stdio.h>
#include <malloc.h>
#define MAXV 100                //最大顶点个数
#define INF 32767               //INF表示∞

typedef int InfoType;

//以下定义邻接矩阵类型
typedef struct
{
    int no;                     //顶点编号
    InfoType info;              //顶点其他信息，在此存放带权图权值
} VertexType;                   //顶点类型

typedef struct                  //图的定义
{
    int edges[MAXV][MAXV];      //邻接矩阵
    int n,e;                    //顶点数，弧数
    VertexType vexs[MAXV];      //存放顶点信息
} MGraph;                       //图的邻接矩阵类型

//以下定义邻接表类型
typedef struct ANode            //弧的结点结构类型
{
    int adjvex;                 //该弧的终点位置
    struct ANode *nextarc;      //指向下一条弧的指针
    InfoType info;              //该弧的相关信息,这里用于存放权值
} ArcNode;

typedef int Vertex;

typedef struct Vnode            //邻接表头结点的类型
{
    Vertex data;                //顶点信息
    int count;                  //存放顶点入度,只在拓扑排序中用
    ArcNode *firstarc;          //指向第一条弧
} VNode;

typedef VNode AdjList[MAXV];    //AdjList是邻接表类型

typedef struct
{
    AdjList adjlist;            //邻接表
    int n,e;                    //图中顶点数n和边数e
} ALGraph;                      //图的邻接表类型

//功能：由一个反映图中顶点邻接关系的二维数组，构造出用邻接矩阵存储的图
//参数：Arr - 数组名，由于形式参数为二维数组时必须给出每行的元素个数，在此将参数Arr声明为一维数组名（指向int的指针）
//      n - 矩阵的阶数
//      g - 要构造出来的邻接矩阵数据结构
void ArrayToList(int *Arr, int n, ALGraph *&); //用普通数组构造图的邻接表
void ExistPath(ALGraph *G,int u,int v, bool &has);
void HasPath(ALGraph *G,int u,int v);
void FindAPath(ALGraph *G,int u,int v,int path[],int d);
void APath(ALGraph *G,int u,int v);
void FindPaths(ALGraph *G,int u,int v,int path[],int d);
void DispPaths(ALGraph *G,int u,int v);
void SomePaths(ALGraph *G,int u,int v,int s, int path[],int d);
void DispSomePaths(ALGraph *G,int u,int v, int s);
void DFSPath(ALGraph *G,int u,int v,int path[],int d);
void FindCyclePath(ALGraph *G,int k);
#endif // GRAPH_H_INCLUDED

#include "graph.h"
void ArrayToList(int *Arr, int n, ALGraph *&G)
{
    int i,j,count=0;  //count用于统计边数，即矩阵中非0元素个数
    ArcNode *p;
    G=(ALGraph *)malloc(sizeof(ALGraph));
    G->n=n;
    for (i=0; i<n; i++)                 //给邻接表中所有头节点的指针域置初值
        G->adjlist[i].firstarc=NULL;
    for (i=0; i<n; i++)                 //检查邻接矩阵中每个元素
        for (j=n-1; j>=0; j--)
            if (Arr[i*n+j]!=0)      //存在一条边，将Arr看作n×n的二维数组，Arr[i*n+j]即是Arr[i][j]
            {
                p=(ArcNode *)malloc(sizeof(ArcNode));   //创建一个节点*p
                p->adjvex=j;
                p->info=Arr[i*n+j];
                p->nextarc=G->adjlist[i].firstarc;      //采用头插法插入*p
                G->adjlist[i].firstarc=p;
            }

    G->e=count;
}
int visited[MAXV];     //定义存放节点的访问标志的全局数组
void ExistPath(ALGraph *G,int u,int v, bool &has)
{
    int w;
    ArcNode *p;
    visited[u]=1;
    if(u==v)
    {
        has=true;
        return;
    }
    p=G->adjlist[u].firstarc;
    while (p!=NULL)
    {
        w=p->adjvex;
        if (visited[w]==0)
            ExistPath(G,w,v,has);
        p=p->nextarc;
    }
}

void HasPath(ALGraph *G,int u,int v)
{
    int i;
    bool flag = false;
    for (i=0; i<G->n; i++)
        visited[i]=0; //访问标志数组初始化
    ExistPath(G,u,v,flag);
    printf(" 从 %d 到 %d ", u, v);
    if(flag)
        printf("有简单路径\n");
    else
        printf("无简单路径\n");
}
void FindAPath(ALGraph *G,int u,int v,int path[],int d)
{
    //d表示path中的路径长度，初始为-1
    int w,i;
    ArcNode *p;
    visited[u]=1;
    d++;
    path[d]=u;  //路径长度d增1，顶点u加入到路径中
    if (u==v)   //找到一条路径后输出并返回
    {
        printf("一条简单路径为:");
        for (i=0; i<=d; i++)
            printf("%d ",path[i]);
        printf("\n");
        return;         //找到一条路径后返回
    }
    p=G->adjlist[u].firstarc;  //p指向顶点u的第一个相邻点
    while (p!=NULL)
    {
        w=p->adjvex;    //相邻点的编号为w
        if (visited[w]==0)
            FindAPath(G,w,v,path,d);
        p=p->nextarc;   //p指向顶点u的下一个相邻点
    }
}

void APath(ALGraph *G,int u,int v)
{
    int i;
    int path[MAXV];
    for (i=0; i<G->n; i++)
        visited[i]=0; //访问标志数组初始化
    FindAPath(G,u,v,path,-1);  //d初值为-1，调用时d++，即变成了0
}
void FindPaths(ALGraph *G,int u,int v,int path[],int d)
//d是到当前为止已走过的路径长度，调用时初值为-1
{
    int w,i;
    ArcNode *p;
    visited[u]=1;
    d++;            //路径长度增1
    path[d]=u;              //将当前顶点添加到路径中
    if (u==v && d>1)            //输出一条路径
    {
        printf("  ");
        for (i=0; i<=d; i++)
            printf("%d ",path[i]);
        printf("\n");
    }
    p=G->adjlist[u].firstarc; //p指向u的第一条边
    while(p!=NULL)
    {
        w=p->adjvex;     //w为u的邻接顶点
        if (visited[w]==0)      //若顶点未标记访问，则递归访问之
            FindPaths(G,w,v,path,d);
        p=p->nextarc; //找u的下一个邻接顶点
    }
    visited[u]=0;   //恢复环境
}


void DispPaths(ALGraph *G,int u,int v)
{
    int i;
    int path[MAXV];
    for (i=0; i<G->n; i++)
        visited[i]=0; //访问标志数组初始化
    printf("从%d到%d的所有路径:\n",u,v);
    FindPaths(G,u,v,path,-1);
    printf("\n");
}
void SomePaths(ALGraph *G,int u,int v,int s, int path[],int d)
//d是到当前为止已走过的路径长度，调用时初值为-1
{
    int w,i;
    ArcNode *p;
    visited[u]=1;
    d++;            //路径长度增1
    path[d]=u;              //将当前顶点添加到路径中
    if (u==v && d==s)           //输出一条路径
    {
        printf("  ");
        for (i=0; i<=d; i++)
            printf("%d ",path[i]);
        printf("\n");
    }
    p=G->adjlist[u].firstarc; //p指向u的第一条边
    while(p!=NULL)
    {
        w=p->adjvex;     //w为u的邻接顶点
        if (visited[w]==0)      //若顶点未标记访问，则递归访问之
            SomePaths(G,w,v,s,path,d);
        p=p->nextarc; //找u的下一个邻接顶点
    }
    visited[u]=0;   //恢复环境
}

void DispSomePaths(ALGraph *G,int u,int v, int s)
{
    int i;
    int path[MAXV];
    for (i=0; i<G->n; i++)
        visited[i]=0; //访问标志数组初始化
    printf("从%d到%d长为%d的路径:\n",u,v,s);
    SomePaths(G,u,v,s,path,-1);
    printf("\n");
}

void DFSPath(ALGraph *G,int u,int v,int path[],int d)
//d是到当前为止已走过的路径长度，调用时初值为-1
{
    int w,i;
    ArcNode *p;
    visited[u]=1;
    d++;
    path[d]=u;
    p=G->adjlist[u].firstarc;   //p指向顶点u的第一条边
    while (p!=NULL)
    {
        w=p->adjvex;            //w为顶点u的相邻点
        if (w==v && d>0)        //找到一个回路，输出之
        {
            printf("  ");
            for (i=0; i<=d; i++)
                printf("%d ",path[i]);
            printf("%d \n",v);
        }
        if (visited[w]==0)          //w未访问，则递归访问之
            DFSPath(G,w,v,path,d);
        p=p->nextarc;       //找u的下一个邻接顶点
    }
    visited[u]=0;           //恢复环境：使该顶点可重新使用
}

void FindCyclePath(ALGraph *G,int k)
//输出经过顶点k的所有回路
{
    int path[MAXV],i;
    for (i=0; i<G->n; i++)
        visited[i]=0; //访问标志数组初始化
    printf("经过顶点%d的所有回路\n",k);
    DFSPath(G,k,k,path,-1);
    printf("\n");
}

#include "graph.h"
int main()
{
    ALGraph *G;
    int A[5][5]=
    {
        {0,0,0,0,0},
        {0,0,1,0,0},
        {0,0,0,1,1},
        {0,0,0,0,0},
        {1,0,0,1,0},
    };  //请画出对应的有向图
    ArrayToList(A[0], 5, G);
    HasPath(G, 1, 0);
    HasPath(G, 4, 1);

    APath(G, 1, 0);
    APath(G, 4, 1);

    DispPaths(G, 1, 4);

    DispSomePaths(G, 1, 4, 3);

    FindCyclePath(G, 0);
    return 0;
}

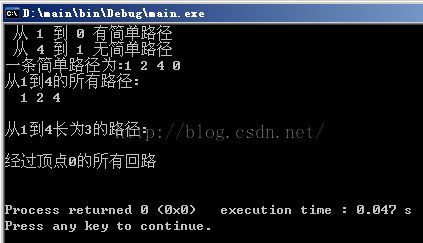
运行结果：

知识点总结：

        （1）设计一个算法，判断顶点u到v是否有简单路径
　　（2）设计一个算法输出图G中从顶点u到v的一条简单路径（设计测试图时，保证图G中从顶点u到v至少有一条简单路径）。
　　（3）输出从顶点u到v的所有简单路径。
　　（4）输出图G中从顶点u到v的长度为s的所有简单路径。
　　（5）求图中通过某顶点k的所有简单回路（若存在）
学习心得：

用算法解决实际问题，首先要明白算法的原理，根据原理写出代码