天平称球问题（一）

前几天在论坛上看到了“八硬币问题”这篇帖子，原文地址是

http://topic.csdn.net/u/20120424/14/3cfdcd2f-671a-475e-8f7a-35663f757fcb.html?49646

由于链接失效了，我再复述一下题目：120个球，其中有一个坏球，用天平称5次，能否找出坏球并知道其轻重？

 

刚看到这个问题，我的第一感觉是分成3个40，先称一次，然后再怎么称就没有头绪了。因为球太多，没有好的方法胡乱试，那不知道要试到什么时候。之前我知道12个球怎么称，但是120个球，怎么称呢？

 

后来看到10楼nice_cxf网友的回答，经过一些思考和总结，决定拿出来和大家分享一下。在此特意先感谢一下nice_cxf网友。不过为了解释的更透彻一点，还是从简单的说起吧。

 

初级版本：

有12个球，其中有一个不知轻重的坏球，用天平称3次，将其找出来，并说明坏球是轻是重？（为了方便描述，将12个球编号为1-9，A-C）

 

方法A（我曾经在某人文集见过的描述）

方法B（根据nice_cxf网友的理论得到的方法）

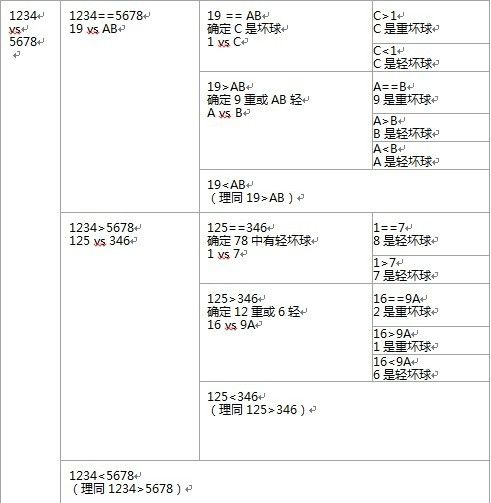
方法C（我的方法）

说到这个方法，还有一段历史，当时是本科，一同学问我12球问题，我在蹲WC时冥思苦想，终于想出来一个办法，然而这个方法当时并没有仔细琢磨，所以后来我就渐渐淡忘了，以至于后来再有人问我这个问题，我都是用方法A回答，这几天经过分析，发现这个方法也可以解决大问题。先给出方法，后面再解释原理。

 

1234  vs  5678

1259  vs  34AB

379A  vs  146C

 

通过这样的3次称量，可以保证每个球无论轻重，都有唯一一种称量结果。