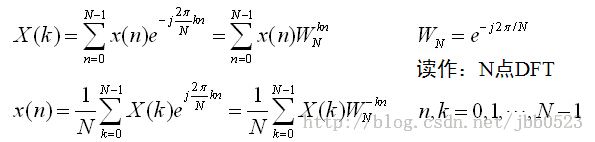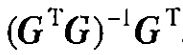Rachel_Zhang的“压缩感知”之“HelloWorld"解读

题目：Rachel_Zhang的“压缩感知”之“”HelloWorld"解读

=================引言====================

看Rachel_Zhang博主的“压缩感知”之“HelloWorld"的Matlab代码有几天了，一直是半知半解，对自己的理解力及数学基础无语了，经过昨晚的琢磨加上今天的理解，算是懂一些了，先写写。

这段代码是香港大学沙威的代码，可以去他的空间看看：http://www.eee.hku.hk/~wsha/Freecode/freecode.htm，里面还有一个中文文档，我读了一遍，感觉写的还挺不错的：“压缩传感”引论 ，里面还有一些其它的资源，打算有空了慢慢琢磨。

还是先把代码贴出来再好好解读吧：

%  1-D信号压缩传感的实现(正交匹配追踪法Orthogonal Matching Pursuit)
%  测量数M>=K*log(N/K),K是稀疏度,N信号长度,可以近乎完全重构
%  编程人--香港大学电子工程系 沙威  Email: [email protected]
%  编程时间：2008年11月18日
%  文档下载: http://www.eee.hku.hk/~wsha/Freecode/freecode.htm 
%  参考文献：Joel A. Tropp and Anna C. Gilbert 
%  Signal Recovery From Random Measurements Via Orthogonal Matching
%  Pursuit，IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 53, NO. 12,
%  DECEMBER 2007.

clc;clear

%%  1. 时域测试信号生成
K=7;      %  稀疏度(做FFT可以看出来)
N=256;    %  信号长度
M=64;     %  测量数(M>=K*log(N/K),至少40,但有出错的概率)
f1=50;    %  信号频率1
f2=100;   %  信号频率2
f3=200;   %  信号频率3
f4=400;   %  信号频率4
fs=800;   %  采样频率
ts=1/fs;  %  采样间隔
Ts=1:N;   %  采样序列
x=0.3*cos(2*pi*f1*Ts*ts)+0.6*cos(2*pi*f2*Ts*ts)+0.1*cos(2*pi*f3*Ts*ts)+0.9*cos(2*pi*f4*Ts*ts);  %  完整信号

%%  2.  时域信号压缩传感
Phi=randn(M,N);                                   %  测量矩阵(高斯分布白噪声)
s=Phi*x.';                                        %  获得线性测量 

%%  3.  正交匹配追踪法重构信号(本质上是L_1范数最优化问题)
m=2*K;                                            %  算法迭代次数(m>=K)
Psi=fft(eye(N,N))/sqrt(N);                        %  傅里叶正变换矩阵
T=Phi*Psi';                                       %  恢复矩阵(测量矩阵*正交反变换矩阵)

hat_y=zeros(1,N);                                 %  待重构的谱域(变换域)向量                     
Aug_t=[];                                         %  增量矩阵(初始值为空矩阵)
r_n=s;                                            %  残差值

for times=1:m;                                    %  迭代次数(有噪声的情况下,该迭代次数为K)
    for col=1:N;                                  %  恢复矩阵的所有列向量
        product(col)=abs(T(:,col)'*r_n);          %  恢复矩阵的列向量和残差的投影系数(内积值) 
    end
    [val,pos]=max(product);                       %  最大投影系数对应的位置
    Aug_t=[Aug_t,T(:,pos)];                       %  矩阵扩充
    T(:,pos)=zeros(M,1);                          %  选中的列置零（实质上应该去掉，为了简单我把它置零）
    aug_y=(Aug_t'*Aug_t)^(-1)*Aug_t'*s;           %  最小二乘,使残差最小
    r_n=s-Aug_t*aug_y;                            %  残差
    pos_array(times)=pos;                         %  纪录最大投影系数的位置
end
hat_y(pos_array)=aug_y;                           %  重构的谱域向量
hat_x=real(Psi'*hat_y.');                         %  做逆傅里叶变换重构得到时域信号

%%  4.  恢复信号和原始信号对比
figure(1);
hold on;
plot(hat_x,'k.-')                                 %  重建信号
plot(x,'r')                                       %  原始信号
legend('Recovery','Original')
norm(hat_x.'-x)/norm(x)                           %  重构误差

其实这段代码注释已经很详细了，下面结合我在看这段代码时被难住的几个地方加以说明。

========================正文========================

首先把代码中的符号说明一下，这样看起来会省力一些：

上标T表示转置，代码中是英文单引号‘表示转置，其它与代码中符号保持一致。

Phi=randn(M,N); 这一句是生成一个测量矩阵，高斯测量矩阵，这个矩阵要和Psi尽可能不相关。

Psi=fft(eye(N,N))/sqrt(N); 这里的稀疏基是一个傅里叶变换矩阵，这里解释一下：

这里得说一下离散傅里叶变换（Discrete Fourier Transform, DFT）:

上面是DFT离散傅里叶变换对，这里只看正变换即第一个由x(n)变到X(k)的式子，这个式子可以写成矩阵形式：

这里，代码中的fft(eye(N,N))就是这里的WN矩阵，这里是对单位阵eye(N,N)做二维FFT变换，在MATLAB里还可以用dftmtx(N)来实现，当然，实际上dftmtx(N)就是由fft(eye(N,N))来实现的，这里使用的稀疏基Psi是对WN除以sqrt(N)归一化的，即快速傅里叶变换基。

好，基础介绍完了，代码的核心其实是for循环实现正交匹配追踪算法（Orthogonal Matching Pursuit，OMP），要想看懂代码，必须知道什么是OMP，这里把代码中提到的参考文献中的OMP流程贴出来：

好了，有了OMP算法，开始对应解释代码：

    for col=1:N;                                  %  恢复矩阵的所有列向量
        product(col)=abs(T(:,col)'*r_n);          %  恢复矩阵的列向量和残差的投影系数(内积值) 
    end

这个循环是让矩阵T的每一列与残差求内各，T一共有N列，这里得到N个内积值存在product里面。内积值最大的即为相关性最强T(:,col)为M*1列向量，r_n初如化为s，是M*1列向量，这里让T(:,col)转置后再与r_n相乘，即一个1*M的行向量与一个M*1的列向量相乘，根据矩阵运算规则结果为一个数（即1*1的矩阵）。

[val,pos]=max(product); 这句话的关键是得到pos，即得到T中的哪一列与残差r_n的内积值最大，也就是哪一列与残差r_n相关性最强。此即 英文步骤中的第二步。

Aug_t=[Aug_t,T(:,pos)]; 此即英文步骤中的第三步，将刚刚得到的与残差r_n内积值最大的列存到Aug_t中，这个矩阵随着循环次数（迭代次数）的变换而变化，是M*times的矩阵。

T(:,pos)=zeros(M,1); 这一句是为了下一次迭代做准备的，这次找到了与残差最相关的列，将残差更新后，下次再找与残差仅次于这一列的T的另外一列；

aug_y=(Aug_t'*Aug_t)^(-1)*Aug_t'*s; 这一句即英文步骤中的第四步，这句加上后面一句也是困扰了我好久两句代码，所以得说说：

首先我们针对的是s=T*hat_y，现在是已知s要求hat_y，现在假如说矩阵T为N*N方阵且满秩（即N个未知数，N个独立的方程），那么很容易知道hat_y=T^-1 * s，其中T^-1表示矩阵T的逆矩阵。但是现在T是一个M*N的扁矩阵，矩阵T没有常规意义上的逆矩阵，这里就有“广义逆”的概念（详情参见国内矩阵分析教材），hat_y的解可能是不存在的，我们这里要求的是最小二乘解aug_y，最小二乘解aug_y将使s-T*aug_y这个列向量2范数最小。

对于用矩阵形式表达的线性方程组：

它的最小二乘解为：

其中

即为矩阵G的最小二乘广义逆（广义逆的一种）。

有了这些知识背景后代码就容易理解了，在第三步中，得到矩阵T中的与残差r_n最相关的列组成的矩阵Aug_t，而第四步实际上就是在求方程组Aug_t*Aug_y=s的最小二乘解。

r_n=s-Aug_t*aug_y;这一句就是用求得的最小二乘解更新残差r_n，在下一次迭代中使用。注意最小二乘解的含义，它并不是使Aug_t*Aug_y=s成立，而只是让s-Aug_t*aug_y的2范数最小，而r_n就是最小的值。此即英文步骤中的第五步，两个式子合在一起写了。

pos_array(times)=pos; 把与T中与残差最相关的列号记下来，恢复时使用。

到此，主要的for循环就说完了。

hat_y(pos_array)=aug_y; 最后一次迭代得到的最小二乘解aug_y即为恢复的值，位置分别对应于迭代中每一次与残差r_s最相关的矩阵T的列号。

hat_x=real(Psi'*hat_y.');此即：

，这里用hat_x以与原如信号x区分，x为原信号，hat_x为恢复的信号。代码中对hat_y取了转置是因为hat_y应该是个列向量，而在代码中的前面hat_y=zeros(1,N); 将其命成了行向量，所以这里转置了一下，没什么大不了的。

到了，到此代码讲完了，为什么这里要用real取实部呢？我不知道，我猜是Psi是一个复矩阵，所以与hat_y乘出来的结果肯定是复数的，所以这里取了实数，但刨根问底：为什么呢？哪位知道的话给留个言，谢谢啦！

压缩感知需要的基础真心多，自己打算先期以看懂各位大牛们的文章为主，所以近期发的博文都以对大牛们的某某博文的理解类型为主……