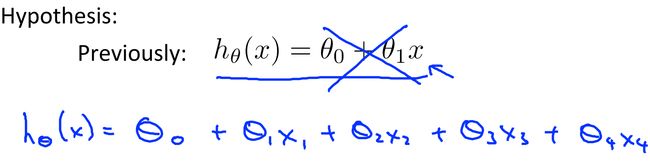斯坦福机器学习公开课笔记(二)--多变量线性回归
公开课地址:https://class.coursera.org/ml-003/class/index
授课老师:Andrew Ng
1、multiple features(多特征)
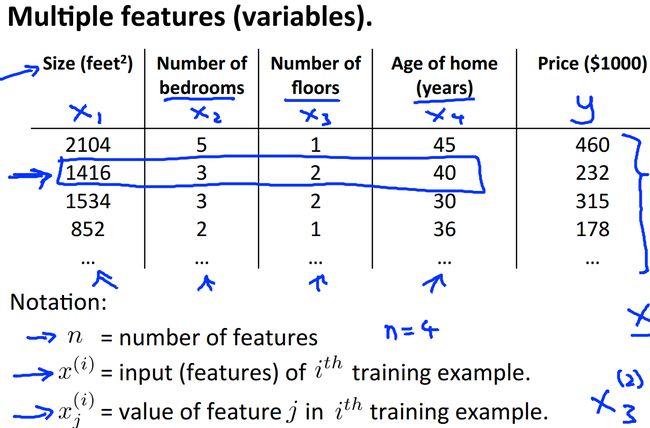
在第一次课中我们假设房屋的价格仅和房屋的面积相关,显然这与实际情况不符,为此,我们需要考虑更多的影响因素,也就是这里说的房屋的特征。比如,我们可以加入房屋中卧室的数量,房屋所在的楼层数和房屋的年龄这几个因素:
显然,我们之前定义的函数形式就作废了,现在需要重新定义函数,这里可以定义多变量的一阶函数。
当然,如果变量再多,可以继续扩展,像下面这样:
这里一共有n个自变量x,theta一共n+1个。如果懂一点线性代数的知识,可以发现这里用向量的乘积来表示函数较好,我们假设存在一个x0=1,然后h就可以写成theta向量和x向量的乘积形式了。
2、gradient descent for multiple variables(多变量梯度下降)
尽管这里是多变量,但梯度下降还是一致的,定义出代价函数,然后迭代下降。由于变量过多,还是用向量形式表现较好:
把J代入得到:
3、gradient descent in practice 1:feature scaling(梯度下降实践之特征缩放)
当增加新特征以后,我们会发现由于单位不同,特征的数量级差距较大,有些特征会因此占据主导地位 ,这与我们希望各个特征之间的影响力应该大体上相近不符。为此,我们需要对特征进行归一化,也就是所谓的特征缩放。
上面是针对房屋面积和卧室数目的归一化,通过除以特征中最大值,我们把这两个特征缩放到[0,1]区间。当然还存在其他的归一化方法,比如下面这种通过减去均值再除以最大值把特征映射到[-0.5,0.5]区间:
4、gradient descent in practice 2:learning rate(梯度下降实践之学习率)
前面提到过在梯度下降中学习率的选择是需要考虑的,每次迭代后我们需要让J不断减少,直到到达一个最小值(以减少0.001为阈值表面收敛):
和之前讲到一样,alpha太大太小都不行
5、features and polynomial regression(特征和多项式回归)
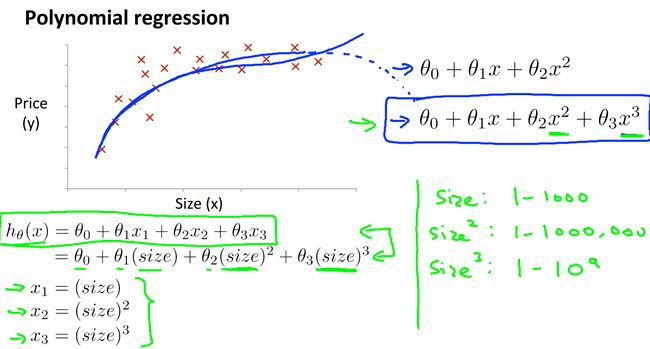
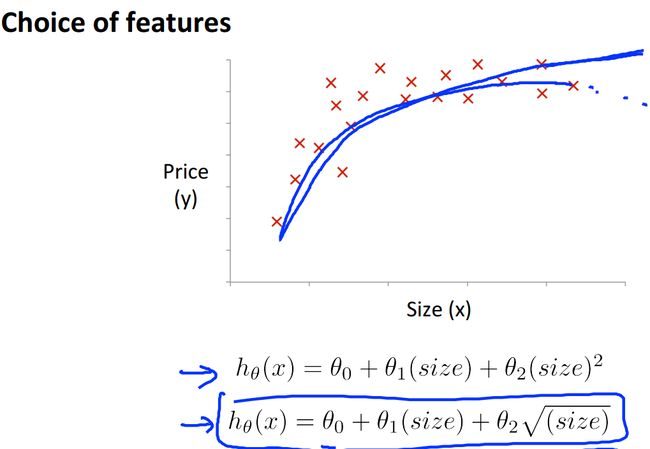
之前我们考虑房价只和面积成线性关系,但是在二维空间中描出点后很可能发现完全不是线性相关的,于是我们要引入特征的高阶属性:
上面就引入了房屋大小的二次方,三次方,当然也可以引入根号,总之函数不再是线性函数那么简单了。
6、normal equation(标准化等式)
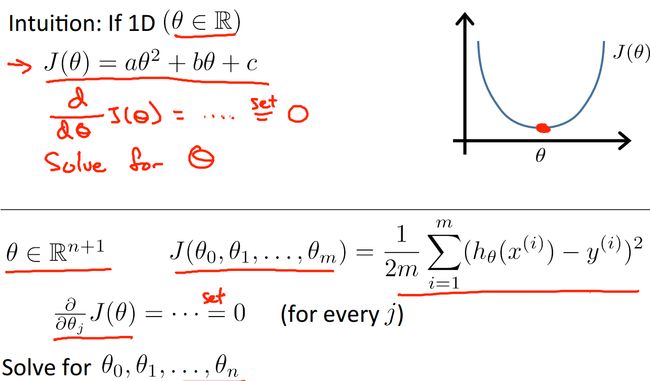
之前介绍的都是梯度下降,其实还有另外一种方法可以用来求解代价函数最小的问题,也就是标准化等式。它是通过解析得到theta的取值,不需要迭代,学过微积分的人都知道如何求一个单变量函数的最值,就是让其求导为0,那肯定是函数的最值点,这就是标准化等式的思想。
再考虑向量化,我们可以把求解转换为向量运算:
这里我们可以把梯度下降和标准化等式做一个对比:
从比较可以发现,标准化在n较大的情况下效果不好,不过其优点是不需要人工设定学习率,也不需要迭代。
7、normal equation non-invertibility(标准化等式不可逆性)
从上面的等式中我们知道计算theta需要求出X’X的逆,但是并不是什么矩阵都可逆的,如果不可逆,我们只能进行特征删除,剔除掉一些冗余的特征,再求解。
-----------------------------------弱弱的分割线-------------------------------------------------
以上就是针对多变量的线性回归,可以看出思想和单变量的差不多,唯一不同的就是要多计算几个值。为了方面,在这里引入了向量的表现形式,同时在计算的时候也应该采用矢量化计算加快计算速度。