一次买卖问题(single sell profit)
问题是这样的,假设有一只股票a,a[1...n]代表股票a在第1到第n天所对应的股价,试找到一对值i,j,满足1<=i<=j<=n,且a[j]-a[i]取得最大值。如下表
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| a | 2 | 7 | 1 | 8 | 2 | 8 | 4 | 5 | 9 | 0 | 4 | 5 |
对于a[1...n],最大正收益并非总可以得到,例如a[1...9]={9,8,7,6,5,4,3,2,1},或者a[9]={0,0,0,0,0,0,0,0,0},对于这样的行情,你在任何不同的两天,进行买入和卖出操作,所得到的都是负收益,或者0,对于此种情况,我们允许i=j,也就是买进的当天卖出,但是不允许i>j的情况出现,也就是先买入,然后才能卖出。下面我就给出这个问题的几个解法。
穷举法
最容易想到的就是该方法,通过穷举a[1...n]中所有天数组和(i,j)(1<=i<=n,i<=j<=n),分别计算a[j]-a[i]的值,所有结果中的最大者,就是最终结果。由于要穷举n个数据的2组和,所以整个算法的时间复杂度为O(n^2)。代码如下
int SingleSellProfit(const int array[], size_t array_size)
{
unsigned int i, j;
int profit = INT_MIN;
for(i = 0; i < array_size; ++i)
{
for(j = i; j < array_size; ++j)
{
if(array[j] - array[i] > profit)
{
profit = array[j] - array[i];
}
}
}
return profit;
}
分治法
O(n^2)的时间复杂度显然不能令我们满意,对于此问题是否有更优的解法呢。对于a[1...n],假设存在k(1<=k<n),将数组分割为两部分a1[1...k],a2[k+1...n],如果我们已知了a1的最大正收益p1和a2的最大正收益p2,那么是否可以计算得到a的最大正收益p呢。
这里需要分三种情况考虑,对于a的最大正收益p,如果买入和卖出时间,均在1~k范围内,那么p=p1,如果买入和卖出时间均在k+1~n范围内,那么p=p2;还有一种情况,就是在1~k范围内某点i买进,在k+1~n范围内的某点j卖出,此时a的最大正收益就等于k+1~n范围内的股价最高点与1~k范围内股价最低点的值的差。所以实际上p的值就等于p1,p2,a[j]-a[i]三者的最大值。利用这个结论,我们就可以利用分治法,将1~n区间内的问题,分解为两个小区间的子问题,通过综合两个小区间子问题的求解结果,得到最终答案。利用递归算法实现代码如下
int Max(int a, int b, int c)
{
if(a >= b && a >= c)
{
return a;
}
if(b >= a && b >= c)
{
return b;
}
if(c >= a && c >= b)
{
return c;
}
}
typedef struct
{
int profit;
unsigned int pmin;//股价最低日期
unsigned int pmax;//股价最高日期
}ret;
ret subRoutine(const int array[], unsigned int begin, unsigned int end)
{
unsigned int middle;
ret r, r1, r2;
if(begin == end)
{
r.profit = 0;
r.pmin = begin;
r.pmax = begin;
return r;
}
middle = (begin + end) / 2;
r1 = subRoutine(array, begin, middle);
r2 = subRoutine(array, middle + 1, end);
r.pmin = array[r1.pmin] < array[r2.pmin] ? r1.pmin : r2.pmin;
r.pmax = array[r1.pmax] > array[r2.pmax] ? r1.pmax : r2.pmax;
r.profit = Max(r1.profit, r2.profit, array[r2.pmax] - array[r1.pmin]);
return r;
}
int SingleSellProfit(const int array[], size_t array_size)
{
ret r = subRoutine(array, 0, array_size -1);
return r.profit;
}
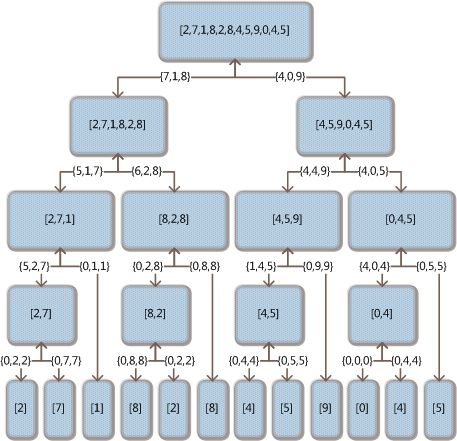
这里需要注意,递归的终止条件就是将a分解为单元素数组时。对于单元素数组,例如a[2]=7,他的最大正收益是a[2]-a[2]=0,股价最高点是a[2]=7,股价最低点也是a[2]=7。对于一个子区间的求解结果,因为无法确定其是与前面的子区间,还是后面的子区间结合生成更大的区间,所以计算过程中,要将该区间的股价最高和最低点都返回。下图说明了使用分治法求解文章开头给出数组的递归调用过程。其中相邻层之间连接线中的数据内容为{下层区间的最大正收益,下层区间的股价最小值,下层区间的股价最大值}
该算法求解一次买卖问题的时间复杂度为O(n),空间复杂度为O(logn)。
递推法
乍看之下,分治法已经是求解该问题的相当理想的解决方案,但是实际上,该问题还有更加犀利的求解算法。假设,我们已经求得a[1...k]中所能获得的最大正收益p,当在该数组的尾部,添加a[k+1]时,我们如何得到a[1...k+1]的最大正收益呢。
对于a[k+1]也有三种情况需要分别处理。
第一种,a[k+1]是卖出点,对于此种情况,假设a[1...k]中的股价最低点为i(1<=i<=k),那么用a[k+1]-a[i],就得到了以a[k+1]为卖出点所能得到的最大正收益,如果该值大于p,那么a[k+1]-a[i]就是数组a[1...k+1]中的最大正收益。
第二种,a[k+1]是买入点,如果a[k+1]是全局最大正收益的可能买入点,那么其对应的卖出点j>=k+1,对于a[1...k+1]而言,p依然是该区间所能得到的最大正收益。但是a[k+1]必须要小于a[1...k]区间中的股价最低点a[i](1<=i<=k),否则的话就有a[j]-a[i]>a[j]-a[k+1],这与a[k+1],是全局最大正收益的买入点矛盾。
第三种,如果不满足上述两种情况,则a[k+1]既不是买入点,也不是卖出点。
有了对上面三种情况的分析,就可以给出该问题的递推算法步骤。
- 令k从1到n递增
- 在k==1时,记录当前的最大正收益p=0,区间股价最低点i=1,递增k。
- 判断a[k]-a[i]与p的大小关系,如果a[k]-a[i]>p,令p=a[k]-a[i],递增k。
- 如果a[k]-a[i]<=p,判断a[k]与a[i]的大小关系,如果a[k]<a[i],令i=k,递增k。
- 依次递推,直到数组尾部为止,p即是所求的最大正收益。
该算法的代码实现如下
int SingleSellProfit(const int array[], size_t array_size)
{
unsigned int i, pmin;
int profit = 0;
for(i = 0, pmin = 0; i < array_size; ++i)
{
if(array[i] - array[pmin] > profit)
{
profit = array[i] - array[pmin];
continue;
}
if(array[i] < array[pmin])
{
pmin = i;
}
}
return profit;
}
该算法可以在O(n)时间复杂度,O(1)空间复杂度情况下,解决该问题。
后记
问题并不复杂,但却是阐释算法精妙的绝佳示例,对于一个问题,研究的越深入,越有可能得到令人振奋的优秀解法。但是通常情况,简单算法直观易懂,代码实现容易,正确性容易保证,不足之处便是时间或空间的复杂度较高。而复杂算法,往往原理难懂,编码实现容易出错,程序正确性不易保证。所以这就要求我们在具体应用中对于具体问题选择合适的解决方案。
以本文的问题为例,如果任务只是要分析一批数据,那么穷举法无疑是较好的选择,不用动太多的脑筋就可以开发出基本正确的程序,将数据处理完,如果使用分治法,没准别人已经出了分析结果,而你还在调试程序,高效算法的优势完全体现不出来。但是如果要做的是一个股票分析软件,需要对成百上千只股票,几年几十年的历史数据进行分析,算法不是要运行几次,而是几十万次,那么就必须对算法的选择认真斟酌,在实际应用中O(n)和O(n^2)的运行时间,相差不是一点点
当然,该问题的第三个解法——递推法,看似给出了一个完美的解决方案,兼具了简洁和效率。但是在实际工作中,对于一个问题,要提出如此优美的解决方法并非易事,需要对问题本身作深入的分析才有可能完成。很多问题的优美解法,往往是在提出若干年后才被发现的,只能说是可遇而不可求。这就像我的这篇文章中介绍的求最大子串和的Kadane算法在问题提出的7年之后才被发现,原理虽不复杂,但也绝非一朝一夕就可以搞出来。由此可见,算法是一门艺术,将算法应用于具体场景也是一门艺术。