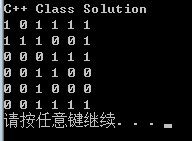
Geeks 面试题： Rat in a Maze 回溯法解迷宫

We have discussed Backtracking and Knight’s tour problem in Set 1. Let us discuss Rat in a Maze as another example problem that can be solved using Backtracking.

A Maze is given as N*N binary matrix of blocks where source block is the upper left most block i.e., maze[0][0] and destination block is lower rightmost block i.e., maze[N-1][N-1]. A rat starts from source and has to reach destination. The rat can move only in two directions: forward and down.
In the maze matrix, 0 means the block is dead end and 1 means the block can be used in the path from source to destination. Note that this is a simple version of the typical Maze problem. For example, a more complex version can be that the rat can move in 4 directions and a more complex version can be with limited number of moves.

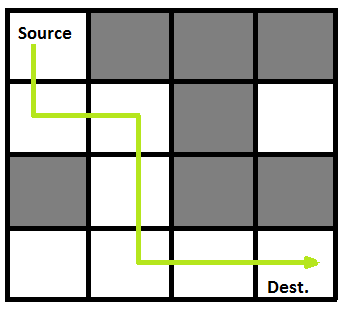
Following is an example maze.

 Gray blocks are dead ends (value = 0). 

Following is binary matrix representation of the above maze.

                {1, 0, 0, 0}
                {1, 1, 0, 1}
                {0, 1, 0, 0}
                {1, 1, 1, 1}

Following is maze with highlighted solution path.

Following is the solution matrix (output of program) for the above input matrx.

                {1, 0, 0, 0}
                {1, 1, 0, 0}
                {0, 1, 0, 0}
                {0, 1, 1, 1}
 All enteries in solution path are marked as 1.

Naive Algorithm
The Naive Algorithm is to generate all paths from source to destination and one by one check if the generated path satisfies the constraints.

while there are untried paths
{
   generate the next path
   if this path has all blocks as 1
   {
      print this path;
   }
}

Backtrackng Algorithm

If destination is reached
    print the solution matrix
Else
   a) Mark current cell in solution matrix as 1. 
   b) Move forward in horizontal direction and recursively check if this 
       move leads to a solution. 
   c) If the move chosen in the above step doesn't lead to a solution
       then move down and check if  this move leads to a solution. 
   d) If none of the above solutions work then unmark this cell as 0 
       (BACKTRACK) and return false.

Backtracking 回溯法的三部曲：

1 初始化原始数据，开始点

2 判断下一步是否合法，如果合法就继续递归搜索答案，如果不合法就返回

3 递归直到找到答案，返回真值

这里只需要找到一个解就可以，所以只要找到一个解就可以马上返回。

Leetcode上很喜欢找出所有解的，那么就需要递归所以可能路径了。

说明一下，原题意是规定往下和往右这两个方向探索的，相当于简化了。

这里给出的程序是可以上下左右四个方向探索的，相当于全功能版的解迷宫了，当然，回溯算法是OK的了，类可以继续扩展。

class Maze
{
	vector<vector<bool> > maze;
	vector<vector<bool> > solMaze;
	int row, col;
public:
	Maze():maze(6), row(6), col(6), solMaze(6, vector<bool>(6))
	{
		bool a[6][6] = {
			{0,1,0,0,0,0},
			{0,0,0,1,1,0},
			{1,1,1,0,0,0},
			{0,0,0,0,1,1},
			{1,1,0,1,0,0},
			{0,0,0,0,0,0}};
		for (int i = 0; i < 6; i++)
		{
			maze[i].assign(a[i], a[i]+6);
		}
	}
	bool isLegal(int x, int y)
	{
		return x>=0 && y>=0 && x<col && y<row && !maze[x][y] && !solMaze[x][y];
	}

	bool solveMaze(int x, int y)
	{
		if (x == col-1 && y == row-1) 
		{
			solMaze[x][y] = 1;
			return true;
		}

		if (isLegal(x, y))
		{
			solMaze[x][y] = 1;

			if (solveMaze(x, y+1)) return true;
			if (solveMaze(x+1, y)) return true;
			if (solveMaze(x-1, y)) return true;
			if (solveMaze(x, y-1)) return true;

			solMaze[x][y] = 0;
		}
		return false;
	}

	void printSolution()
	{
		for (auto x:solMaze)
		{
			for (auto y:x)
				cout<<y<<" ";
			cout<<endl;
		}
	}
};

int main()
{
	cout<<"C++ Class Solution\n";
	Maze ma;
	ma.solveMaze(0,0);
	ma.printSolution();

	system("pause");
	return 0;
}