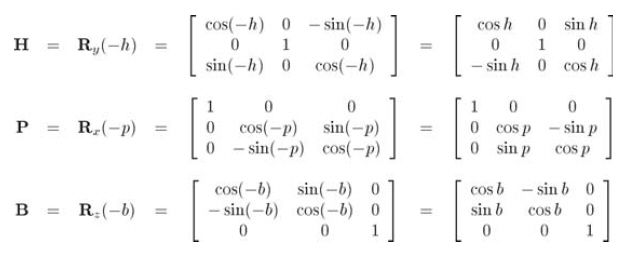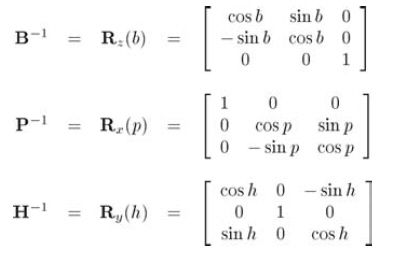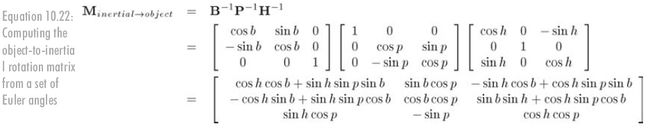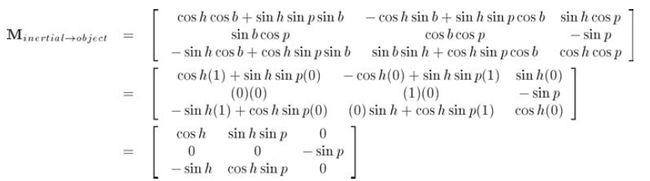3D中的方位和角位移（6）

3D中的方位和角位移（6）

新建网页 1

　

四元数样条 ---- “squad”

Slerp提供了两个方位间的插值，当有多于两个的方位序列（它描述了我们想要经过的插值“路径”）时怎么办？我们可以在”控制点“之间使用slerp。类似于基本几何学中的线性插值，控制点之间是以直线连接的。显然，控制点上会有不连续性 ---- 这是我们想要避免的，我们给出squad(Spherical and Quadrangle)的公式，用来描绘控制点间的路径。

设控制点由四元数序列所定义：

q₁，q₂，q₃，…q_n-2，q_n-1，q_n

另外，引进一个辅助四元数s_i，将它作为临时控制点：

注意，q_i-1至q_i+1计算出s_i，所以s₁和s_n是未定义的。换句话说，曲线从q₂延伸到q_n-1，第一个和最后一个控制点仅用于控制中间的曲线。如果曲线一定要经过这两点，必须在头部和尾部增加虚控制点，一个显而易见的方法就是复制这两个控制点。

给定四个相邻的控制点，squad用于计算中间两点间的插值，这点非常像三次样条。

设四个控制点为： q_i-1，q_i，q_i+1，q_i+2

还要引入一个插值变量h，h从0变化到1时，squad描绘q_i到q_i+1之间的曲线。

整条插值曲线能够分段应用squad方法来获得，如公式10.12所示：

　

四元数的优点和缺点

四元数有一些其他角位移表示方法所没有的优点：

（1）平滑插值。slerp和squad提供了方位间的平滑插值，没有其他方法能提供平滑插值。

（2）快速连接和角位移求逆。四元数叉乘能将角位移序列转换为单个角位移，用矩阵作同样的操作明显会慢一些。四元数共轭提供了一种有效计算反角位移的方法，通过转置旋转矩阵也能达到同样的目的，但不如四元数来得容易。

（3）能和矩阵形式快速转换。四元数和矩阵间的转换比欧拉角与矩阵之间的转换稍微快一点。

（4）仅用四个数。四元数仅包含4个数，而矩阵用了9个数，它比矩阵"经济"得多（当然仍然比欧拉角多33%）。

要获得这些优点是要付出代价的，四元数也有和矩阵相似的问题，只不过问题程度较轻：

（1）比欧拉角稍微大一些。这个额外的数似乎没有太大关系，但在需要保存大量角位移时，如存储动画数据，这额外的33%也是数量可观的。

（2）四元数可能不合法。坏的输入数据或浮点数舍入误差积累都可能使四元数不合法（能通过四元数标准化解决这个问题，确保四元数为单位大小）。

（3）难于使用。在所有三种形式中，四元数是最难于直接使用的。

　

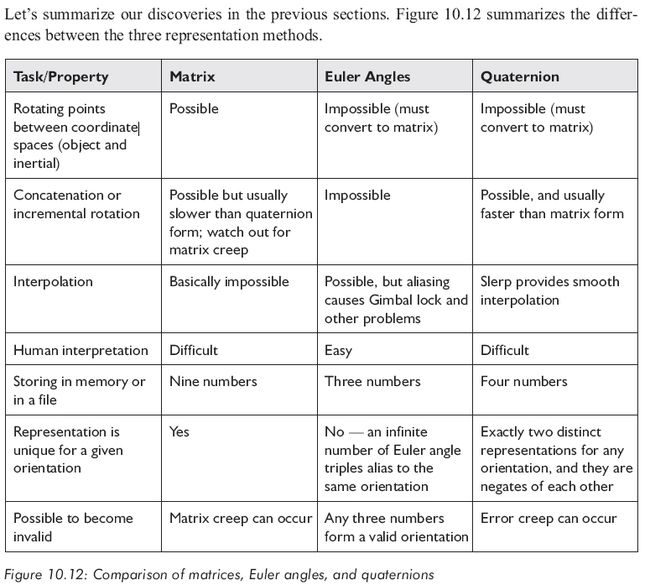
各方法比较

　

不同的方位表示方法适用于不同的情况，下面是我们对合理选择格式的一些建议：

（1）欧拉角最容易使用。当需要为世界中的物体指定方位时，欧拉角能大大简化人机交互，包括直接的键盘输入方位、在代码中指定方位（如为渲染设定摄像机）、在调试中测试。这个优点不应被忽视，不要以优化为名义而牺牲易用性，除非你确定这种优化的确有效果。

（2）如果需要在坐标系间转换向量，那么就选择矩阵形式。当然，这并不意味着你就不能用其他格式来保存方位，并在需要的时候转换到矩阵形式。另一种方法是用欧拉角作为方位的主拷贝，但同时维护一个旋转矩阵，当欧拉角发生改变时矩阵也要同时进行更新。

（3）当需要大量保存方位数据（如动画）时，就使用欧拉角或四元数。欧拉角将少占用25%的内存，但它在转换到矩阵时要稍微慢一些。如果动画数据需要嵌套坐标系之间的连接，四元数可能是最好的选择。

（4）平滑的插值只能用四元数完成。如果你用其他格式，也可以先转换到四元数然后再插值，插值完毕后再转换回原来的形式。

　

　

从欧拉角转换到矩阵

欧拉角描述了一个旋转序列。分别计算出每个旋转的矩阵再将它们连接成一个矩阵，这个矩阵就代表了整个角位移。当然，它和我们是想要物体到惯性坐标的变换矩阵还是惯性到物体坐标的变换矩阵是相关的。

我们对欧拉角的定义是一个旋转序列，该旋转序列将物体（和它的坐标空间）从惯性坐标空间转换到物体坐标空间。因此，可以用欧拉角定义的直接转换来直接产生惯性 ---- 物体旋转矩阵的一般形式：

M_{惯性 --> 物体} = HPB

H、P、B分别为heading、pitch、bank的旋转矩阵，它们分别绕y、x、z轴旋转，仅仅旋转"坐标空间"就是旋转"点"的严格相反操作。可以想象这些旋转发生时点是固定在空间中不变的，例如，pitch使坐标空间向下，点实际上关于坐标空间向上。欧拉角公式明确指明是物体和它的坐标空间旋转，但我们需要的是变换"点"的矩阵，所以计算矩阵H、P、B时，用相反的旋转量来旋转。设heading、pitch、bank的旋转角分别为变量h、p、b:

　

以适当的顺序连接这些矩阵得到公式10.21：

如果要从物体坐标空间变换到惯性坐标空间，应该使用惯性----物体旋转矩阵的逆。因为旋转矩阵是正交的，所以求它的逆就是求它的转置，下面验证这一点。

为了从物体坐标空间变换到惯性坐标空间，顺序应该为"un-bank"、"un-pitch"、"un-heading"，公式表示为：

M_{物体->惯性} = （M_{惯性->物体}）^-1 = （HPB）^-1 = B^-1P^-1H^-1

注意，可以认为旋转矩阵B^-1、P^-1、H^-1为它们对应矩阵的逆，或者是使用相反旋转角b、p、h的一般旋转矩阵。（惯性 --- 物体矩阵中，使用负的旋转角，因此这里的角不用变负。）

以适当的顺序连接这些矩阵得到公式10.22:

比较公式10.21和公式10.22，可以看到物体---惯性矩阵确实惯性---物体矩阵的转置。

　

从矩阵转换到欧拉角

将角位移从矩阵形式转换到欧拉角需要考虑以下几点：

（1）必须清楚矩阵代表什么旋转：物体 -- 惯性还是 惯性 -- 物体，这里讨论使用惯性 -- 物体矩阵的技术，物体 -- 惯性矩阵转换成欧拉角的过程与之类似。

（2）对任意给定角位移，存在无穷多个欧拉角可以用来表示它。因为"别名"问题，这里讨论的技术总是返回"限制欧拉角"，heading和bank的范围±180^°，pitch的范围为±90^°。

（3）矩阵可能是病态的，我们必须忍受浮点数精度的误差。有些矩阵还包括除旋转外的变换，如缩放、镜像等。这里只讨论工作在旋转矩阵上的变换。

考虑这些因素后，我们尝试从公式10.21直接解得欧拉角：

If cos p = 0, then we cannot use the above trick since all the matrix elements involved are zero.
However, notice that when cos p = 0, then p = 90°, which means we are either looking straight
up or straight down. This is the Gimbal lock situation, where heading and bank effectively rotate
about the same physical axis (the vertical axis). In this case, we will arbitrarily assign all rotation
about the vertical axis to heading and set bank equal to zero. Now we know the value of pitch and
bank, and all we have left is to solve for heading. Armed with the following simplifying
assumptions:

cosp = 0

b = 0

sinb = 0

cosb = 1

将它们代入公式10.21:

　

现在，能够通过-m₃₁和m₁₁计算h，它们分别包含了h的sin和cos值。

让我们看看使用上面的技术从惯性 ---- 物体旋转矩阵中抽取欧拉角的代码，为了使示例简单，假设输入输出为全局变量。

     Listing 10.3: Extracting Euler angles from an inertial-to- object  rotation matrix
   
     // Assume the matrix is stored in these variables:
    float  m11,m12,m13;
    float  m21,m22,m23;
    float  m31,m32,m33;
   
        // We will compute the Euler angle values in radians and store them here:
    float  h,p,b;
   
        // Extract pitch from m23, being careful for domain errors with asin(). We could have
    // values slightly out of range due to floating point arithmetic.
    float  sp = –m23;
   
    if  (sp <= –1.0f) {
      p = –1.570796f;  // –pi/2
    }  else   if  (sp >= 1.0) {
      p = 1.570796;  // pi/2
    }  else  {
      p = asin(sp);
    }
   
    // Check for the Gimbal lock case, giving a slight tolerance
    // for numerical imprecision
    if  (sp > 0.9999f) {
       // We are looking straight up or down.
      // Slam bank to zero and just set heading
      b = 0.0f;
      h = atan2(–m31, m11);
    }  else  {
       // Compute heading from m13 and m33
      h = atan2(m13, m33);
   
       // Compute bank from m21 and m22
      b = atan2(m21, m22);
    }