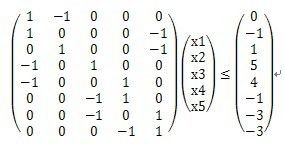差分约束系统详解

差分约束系统详解

 

差分约束系统

    在一个差分约束系统(system of difference constraints)中，线性规划矩阵A的每一行包含一个1和一个-1，A的其他所有元素都为0。因此，由Ax≤b给出的约束条件是m个差分约束集合，其中包含n个未知量，对应的线性规划矩阵A为m行n列。每个约束条件为如下形式的简单线性不等式：xj-xi≤bk。其中1≤i,j≤n，1≤k≤m。

    例如，考虑这样一个问题，寻找一个5维向量x=(xi)以满足：

 

    这一问题等价于找出未知量xi，i=1,2,…,5，满足下列8个差分约束条件：

x1-x2≤0

x1-x5≤-1

x2-x5≤1

x3-x1≤5

x4-x1≤4

x4-x3≤-1

x5-x3≤-3

x5-x4≤-3

    该问题的一个解为x=(-5,-3,0,-1,-4)，另一个解y=(0,2,5,4,1)，这2个解是有联系的：y中的每个元素比x中相应的元素大5。

 
引理：设x=(x1,x2,…,xn)是差分约束系统Ax≤b的一个解，d为任意常数。则x+d=(x1+d,x2+d,…,xn+d)也是该系统Ax≤b的一个解。

 

约束图

   在一个差分约束系统Ax≤b中，m X n的线性规划矩阵A可被看做是n顶点，m条边的图的关联矩阵。对于i=1,2,…,n，图中的每一个顶点vi对应着n个未知量的一个xi。图中的每个有向边对应着关于两个未知量的m个不等式中的一个。

   给定一个差分约束系统Ax≤b，相应的约束图是一个带权有向图G=(V,E)，其中V={v0,v1,…,vn}，而且E={ (vi,vj) : xj-xi≤bk是一个约束}∪{ (v0,v1) , (v0,v2) , … , (v0,vn) }。引入附加顶点v0是为了保证其他每个顶点均从v0可达。因此，顶点集合V由对应于每个未知量xi的顶点vi和附加的顶点v0组成。边的集合E由对应于每个差分约束条件的边与对应于每个未知量xi的边(v0,vi)构成。如果xj-xi≤bk是一个差分约束，则边(vi,vj)的权w(vi,vj)=bk（注意i和j不能颠倒），从v0出发的每条边的权值均为0。

  
定理：给定一差分约束系统Ax≤b，设G=(V,E)为其相应的约束图。如果G不包含负权回路，那么x=( d(v0,v1) , d(v0,v2) , … , d(v0,vn) )是此系统的一可行解，其中d(v0,vi)是约束图中v0到vi的最短路径(i=1,2,…,n)。如果G包含负权回路，那么此系统不存在可行解。

 

差分约束问题的求解

   由上述定理可知，可以采用Bellman-Ford算法对差分约束问题求解。因为在约束图中，从源点v0到其他所有顶点间均存在边，因此约束图中任何负权回路均从v0可达。如果Bellman-Ford算法返回TRUE，则最短路径权给出了此系统的一个可行解；如果返回FALSE，则差分约束系统无可行解。

   关于n个未知量m个约束条件的一个差分约束系统产生出一个具有n+1个顶点和n+m条边的约束图。因此采用Bellman-Ford算法，可以再O((n+1)(n+m))=O(n^2+nm)时间内将系统解决。此外，可以用SPFA算法进行优化，复杂度为O(km)，其中k 为常数。

http://acm.pku.edu.cn/JudgeOnline/problem?id=1364

Description

Once, in one kingdom, there was a queen and that queen was expecting a baby. The queen prayed: ``If my child was a son and if only he was a sound king.'' After nine months her child was born, and indeed, she gave birth to a nice son.
Unfortunately, as it used to happen in royal families, the son was a little retarded. After many years of study he was able just to add integer numbers and to compare whether the result is greater or less than a given integer number. In addition, the numbers had to be written in a sequence and he was able to sum just continuous subsequences of the sequence.

The old king was very unhappy of his son. But he was ready to make everything to enable his son to govern the kingdom after his death. With regards to his son's skills he decided that every problem the king had to decide about had to be presented in a form of a finite sequence of integer numbers and the decision about it would be done by stating an integer constraint (i.e. an upper or lower limit) for the sum of that sequence. In this way there was at least some hope that his son would be able to make some decisions.

After the old king died, the young king began to reign. But very soon, a lot of people became very unsatisfied with his decisions and decided to dethrone him. They tried to do it by proving that his decisions were wrong.

Therefore some conspirators presented to the young king a set of problems that he had to decide about. The set of problems was in the form of subsequences Si = {aSi, aSi+1, ..., aSi+ni} of a sequence S = {a1, a2, ..., an}. The king thought a minute and then decided, i.e. he set for the sum aSi + aSi+1 + ... + aSi+ni of each subsequence Si an integer constraint ki (i.e. aSi + aSi+1 + ... + aSi+ni < ki or aSi + aSi+1 + ... + aSi+ni > ki resp.) and declared these constraints as his decisions.

After a while he realized that some of his decisions were wrong. He could not revoke the declared constraints but trying to save himself he decided to fake the sequence that he was given. He ordered to his advisors to find such a sequence S that would satisfy the constraints he set. Help the advisors of the king and write a program that decides whether such a sequence exists or not.

Input

The input consists of blocks of lines. Each block except the last corresponds to one set of problems and king's decisions about them. In the first line of the block there are integers n, and m where 0 < n <= 100 is length of the sequence S and 0 < m <= 100 is the number of subsequences Si. Next m lines contain particular decisions coded in the form of quadruples si, ni, oi, ki, where oi represents operator > (coded as gt) or operator < (coded as lt) respectively. The symbols si, ni and ki have the meaning described above. The last block consists of just one line containing 0.

Output

The output contains the lines corresponding to the blocks in the input. A line contains text successful conspiracy when such a sequence does not exist. Otherwise it contains text lamentable kingdom. There is no line in the output corresponding to the last ``null'' block of the input.

Sample Input

4 2
1 2 gt 0
2 2 lt 2
1 2
1 0 gt 0
1 0 lt 0
0

Sample Output

lamentable kingdom
successful conspiracy

Source

Central Europe 1997

很典型的差分约束，关键在于怎么构图。
这里我们设Sum(i) = A₁ + A₂ + … + A_i-1
那么输入的si ni oi ki
就可以转换成如下的约束式：Sum(si+ni+1) - Sum(si) oi ki

#include  < iostream >
using   namespace  std;

const   int  MAXN  =   120 ;
const   int  inf  =   0x7f ;
struct  node {
    int s,e,v;
} edge[MAXN];
int  n,m,d[MAXN];

bool  bellman_ford() {
    int i,j;
    for(i=0;i<=n+1;i++) d[i]=inf;
    for(d[0]=0,i=1;i<=n+1;i++)
        for(j=0;j<=(n+m);j++)
            if(d[edge[j].s]+edge[j].v<d[edge[j].e])
                d[edge[j].e]=d[edge[j].s]+edge[j].v;
    for(i=0;i<=(n+m);i++)
        if(d[edge[i].s]+edge[i].v<d[edge[i].e])
            return false;
    return true;
}
int  main() {
    char oi[5];
    int si,ni,k,i,j;
    while(scanf("%d",&n),n){
        scanf("%d",&m);
        for(i=0;i<m;i++){
            scanf("%d %d\n",&si,&ni);
            scanf("%s %d",oi,&k);
            if(oi[0]=='g')
                edge[i].s=si,edge[i].e=si+ni+1,edge[i].v=-k-1;
            else
                edge[i].s=si+ni+1,edge[i].e=si,edge[i].v=k-1;
        }
        for(i=1,j=m;i<=n+1;i++,j++)
            edge[j].s=0,edge[j].e=i,edge[j].v=0;
        puts(bellman_ford()?"lamentable kingdom":"successful conspiracy");
    }
    return 0;
}