基本数据结构(栈和队列)
编程基础文章目录:
| 五大基础算法 | 基础数据结构(栈和队列) | 散列表 |
| 常见C++知识 | 基础数据结构(数组、串、广义表) | 四大比较排序算法 |
| 基础数据结构(线性表) | 基础数据结构(树和堆) |
栈、队列、优先级队列和双端队列是两种特殊的线性表,它们的逻辑结构和线性表相同,只是其运算规则教线性表有更多的限制,故又称为运算受限的线性表。
栈
栈是一种最常用和最重要的数据结构,它的用途非常广泛。例如,汇编处理程序中的句法识别和表达式计算就是基于栈实现的。栈还经常用于函数调用时的参数传递和函数值返回。
栈(stack)可定义为只允许在表的末端进行插入和删除的线性表。允许插入和删除的一端叫做栈顶,而不允许插入和删除的另一端叫做栈底。
栈又叫做后进先出(LIFO)的线性表。
栈的类定义如下:
const int maxSize = 50;
template <class T>
class Stack
{
public:
Stack();
virtual void Push(const T& x) = 0; //新元素x进栈
virtual void Pop(T& x) = 0; //栈顶元素x出栈,由x返回
virtual bool getTop(T& x) const = 0; //
virtual bool IsEmpty() const = 0;
virtual bool IsFull() const = 0;
virtual int getSize() const = 0;
};
栈的抽象数据类型有两种典型的存储表示:
- 基于数组的存储表示:顺序栈
- 基于链表的存储表示:链式栈
顺序栈
顺序栈可以采用顺序表作为其存储表示,为此,可以在顺序栈的声明中用顺序表定义它的存储空间。
顺序顺序栈的类定义:
const int stackIncreament = 20;
template <class T>
class SeqStack:public Stack<T>
{
public:
SeqStack(int sz = 50);
~SeqStack(){delete []elements;};
void Push(const T& x);
bool Pop(T& x);
bool getTop(T& x);
bool IsEmpty()const {return (top == -1) ? true : false};
bool IsFull()const {return (top == maxSize-1) ? true : false};
int getSize()const{return top+1};
void MakeEmpty(){top = -1};
friend ostream& operator << (ostream& os, SeqStack<T>&s){
//输出栈中元素的重载操作<<
}
private:
T *elements;
int top;
int maxSize;
void overflowProcess();
};
栈的构造函数用于在建立栈的对象时为栈的数据成员赋初值。函数中动态建立的栈数组的最大尺寸为maxSize,由函数参数sz给出,并令top=-1,置栈为空。在这个函数实现中,使用了一种断言(Assert)机制,这是C++提供的一种功能,若断言语句assert参数表中给定的条件满足,则继续执行后续的语句;否则出错处理,终止程序的执行。这种断言机制格式简洁,逻辑清晰,不但降低了程序的复杂性,而且提高了程序的可读性。
template <class T>
SeqStack<T> ::SeqStack(int sz):top(-1),maxSize(sz){
//建立一个最大尺寸为sz的空栈,若分配不成功则错误处理;
elements = new T[maxSize];
assert(elements != NULL);
}
扩充栈的存储空间的函数实现:
template <class T>
void SeqStack<T>::overflowProcess(){
T *newArray = new T[maxSize + stackIncreament];
if(newArray = NULL){cerr<<"存储分配失败!"<<endl;exit(1);}
for(int i = 0;i<=top;i++)
newArray[i] = elements[i];
maxSize = maxSize + stackIncreament;
delete []elements;
elements = newArray;
}

当栈满时要发生溢出,为了避免这种情况,需要为栈设立一个足够大的空间。但如果空间设置得过大,而栈中实际只有几个元素,也是一种空间浪费。此外,程序中往往同时存在几个栈,因为各个栈所需的空间在运行时时动态变化着的。如果给几个栈分配同样大小的空间,可能在实际运行中,有的栈膨胀得很快,而其他栈可能此时还有许多空闲的空间。这时就必须调整栈的空间,防止栈的溢出。
例如,程序同时需要两个栈时,我们可以定义一个足够的栈空间。该空间的两端分别设为两个栈的栈底,用b[0](=-1)和b[1](=maxSize)指示。让两个栈的栈顶t[0]和t[1]都向中间伸展,直到相遇,才认为发生溢出。
n(n>2)个栈的情形有所不同,这个时候采用链接方式作为栈的存储表示。
链式栈
链式栈是线性表的链接存储。采用链式栈来表示一个栈,便于结点的插入与删除。在程序中同于使用多个栈的情况下,用链接表示不仅能够提高效率,还可以达到共享存储空间的目的。
top -> [an | ]-> [an-1 | ] -> ....->[a1 | ]
链式栈的栈顶在链表的表头。因此,新结点的插入和栈顶结点的删除都在链表的表头,即栈顶进行。
#include <iostream>
template <class T>
class LinkedStack:public Stack<T>
{
public:
LinkedStack():top(NULL);
~LinkedStack(){makeEmpty();};
void Push(const T& x);
bool Pop(T& x);
bool getTop(T& x)const;
bool IsEmpty()const{return (top == NULL) ? true : false};
int getSize() const;
void makeEmpty();
friend ostream& operator<<(ostream& os, SeqStack<T>& s);
private:
LinkNode<T> *top;
};
template <class T>
Linked<T>::makeEmpty(){
LinkNode<T> *p;
while(top != NULL)
{p = top; top = top ->link;delete p;}
};
template <class T>
void LinkedStack<T>::Push(const T& x){
top = new LinkNode<T>(x,top);
assert(top != NULL);
};
template <class T>
bool LinkedStack<T>::Pop(T &x)
{
if(IsEmpty() == true) return false;
LinkNode<T> *p = top;
top = top->link;
x = p->data;
delete p;
return true;
};
template <class T>
bool LinkedStack<T>::getTop()const{
if(IsEmpty() == true) return false;
x = top->data;
return true;
};
template<class T>
int LinkedStack<T>::getSize() const{
LinkNode<T>*p = top;
int k = 0;
while(top != NULL){top = top->link;k++;}
return k;
};
例题1:括号的匹配
建立一个算法,输入一个字符串,输出匹配的括号和没有匹配的括号。
#include <iostream.h>
#include <string.h>
#include <stdio.h>
#include "stack.h"
const int maxLength = 100;
void PrintMatchedPairs(char *expression)
{
Stack<int> s(maxLength);
int j, length = strlen(expression);
for (int i = 1; i < length; i++){
if(expression[i-1] == "(") s.Push(i);
else if (expression[i-1] == ")"){
if(s.Pop(j) == true)
cout<<j<<"与"<<i<<"匹配"<<endl;
else cout<<"没有与第"<<i<<"个括号匹配的左括号!"<<endl;
}
while(s.IsEmpty() == false){
s.Pop(j);
cout<<"没有与第"<<j<<"个左括号相匹配的右括号!"<<endl;
}
}
}
递归工作栈
每一层递归调用所需保存的信息构成一个工作记录。通常包括如下内容:
- 返回地址:即上一层中调用自己的语句的后续语句处
- 在本次过程调用时,为与形参结合的实参创建副本。包括传值参数和传值返回值的副本空间,引用型参数和引用型返回值的地址空间。
- 本层的局部变量值
用回溯法求解迷宫问题
回溯法(backtracking)也称为试探法。
这种方法将问题的候选解按某种顺序逐一枚举和检验。当发现当前的候选解不可能是解时,就放弃它而选择下一个候选解。若当前的候选解除了不满足问题规模要求外,其他所有要求都已满足,则扩大当前候选解的规模继续试探。
在回溯法中,放弃当前候选解,寻找下一个候选解的过程叫做回溯。扩大当前候选解的规模并继续试探叫做向前试探。
队列
队列只允许在表的一端插入,在表的另一端删除。允许插入的一端叫做队尾(rear),允许删除的一端叫做队尾(front)
先进先出FIFO
队列的存储表示也有两种方式:一种是基于数组的存储表示,另一种是基于链表的存储表示
顺序队列(基于数组存储)
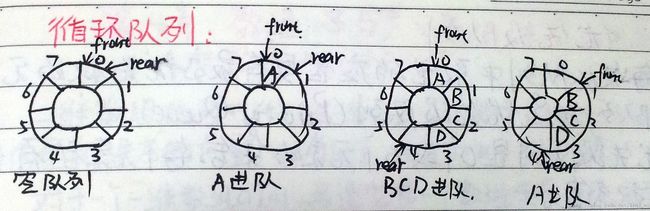
为了能够充分地使用数组中的存储空间,把数组的前端和后端连接起来,形成一个环形的表,即把存储队列元素的表从逻辑上看成一个环,形成循环队列。
循环队列的首尾相接,当队头指针front和队尾指针rear进到maxSize-1后,再前进一个位置就自动到0,实现:
front = (front + 1)% maxSize;
rear = (rear + 1)% maxSize;
如果循环队列读取元素的速度快于存入元素的速度,队头指针很快追上队尾指针,一旦到了front == rear时变成空队列。反之,如果队列存入元素的速度快于读取元素的速度,则队尾指针很快就赶上队头指针,一旦堆满就不能再加入新元素。
(rear+1)%maxSize == front
就是说让rear指到front的前一个位置就认为队满。
链式队列
是基于单链表的一种存储表示
用单链表表示的链式队列特别适合于数据元素变动比较大的情形,而且不存在队列满而产生溢出的情况。
优先级队列
每次从队列中取出的应是具有最高优先权的元素,这种队列就是优先级队列(Priority Queue)
优先级队列是0个或多个元素的集合,每个元素都有一个优先权或值。