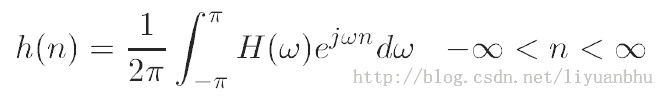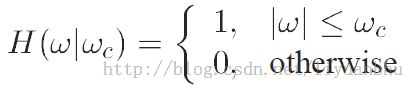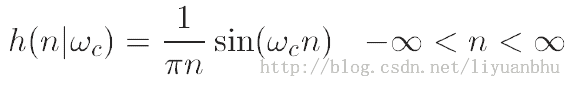利用 SCILAB 设计 FIR 滤波器(窗函数法)
理论上说,设计FIR滤波器是很简单的,给定一个期望的频率响应H(ω),对其进行傅里叶反变换就可以得到FIR滤波器的离散单位冲击响应。
实际使用中的问题是,这样得到的许多滤波器的滤波器阶数都是无穷的而且得到的滤波器不一定是因果系统。
比如理想低通滤波器,截止频率为ωc
计算得到的滤波器系数为:
一种简单的办法是将这个序列中间的一部分截取出来。也就是对信号加一个矩形的窗函数。
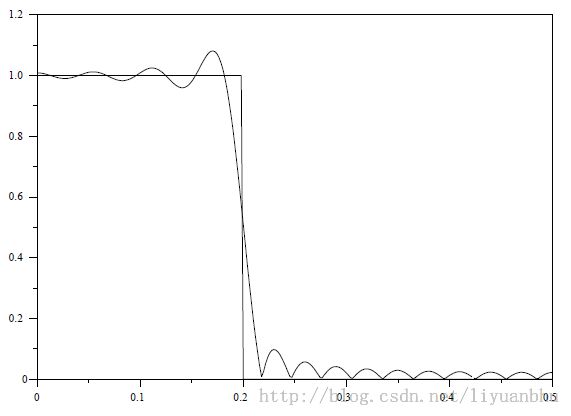
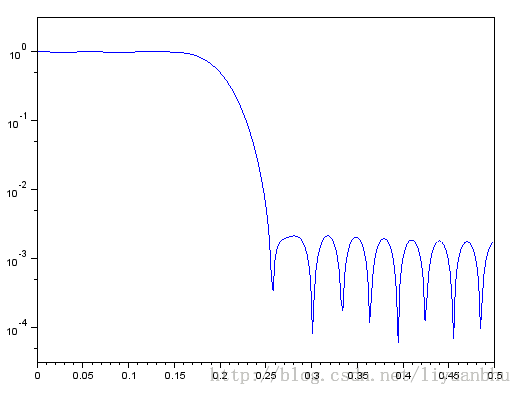
当N = 33 截止频率ωc =0.2时滤波器的频率响应如下图所示,其中实线是理想低通滤波器的响应曲线。加窗的结果是频响曲线在通频带和阻带都产生了波动,偏离理想低通滤波器频响曲线最大的地方在ωc处。
除了用矩形窗函数,还可以采用其他形状的窗函数,不同类型的窗函数有不同的特点。关于不同窗函数的特征请参见数字信号处理方面的教材,这里不多说了。
wfir
[wft,wfm,fr]=wfir(ftype,forder,cfreq,wtype,fpar)
Ftype 表示滤波器的类型,可以为'lp','hp','bp','sb'
Forder 为滤波器的阶数
Cfreq 为滤波器的转折频率,对于低通和高通滤波器来说提供一个截止频率就行了,对于带通和带阻滤波器要提供2个转折频率。这里的频率都是归一化了的,采样频率被归一化为1。
所以转折频率要小于 0.5。
Wtype 表示窗函数的类型,可以为 're','tr','hm','hn','kr','ch'
Fpar 表示窗函数的参数,长度为2的数组,只对 Kaiser 窗 和Chebyshev 窗有效。
对 Kaiser 窗fpar(1)>0, fpar(2)=0.
对Chebyshev 窗fpar(1)>0, fpar(2)<0 或者 fpar(1)<0, 0<fpar(2)<.5
返回值:
Wft 为返回的滤波器系数
Wfm 为滤波器的频响特性
Fr 为Wfm 对应的频率点
下面举一个具体的例子:
[h,hm,fr]=wfir("lp",33,[.2 0],"hm",[0 0]);
这个表示低通滤波器,33阶,截止频率0.2,hamming 窗
Plot(fr,hm);
窗函数法设计FIR滤波器器介绍这些也就差多不了,下次介绍频率抽样法。