Collaborative filtering with GraphChi

原文链接：Collaborative filtering with GraphChi

本文是GraphChi平台的协同过滤工具箱的快速指南。到目前为止，已经支持ALS（最小二乘法）、SGD（随机梯度下降）、bias-SGD（带偏置的随机梯度下降）、SVD++、NMF（非负矩阵分解）、SVD（restarted Lanczos、one sided Lanczos，svd可以参考leftnoeasy的博客），并将实现更多的算法。

以下是这些方法所对应的论文：

Alternating Least Squares (ALS)

• Yunhong Zhou, Dennis Wilkinson, Robert Schreiber and Rong Pan. Large-Scale Parallel Collaborative Filtering for the Netflix Prize. Proceedings of the 4th international conference on Algorithmic Aspects in Information and Management. Shanghai, China pp. 337-348, 2008.
  

• Stochastic gradient descent (SGD)

   Matrix Factorization Techniques for Recommender Systems Yehuda Koren, Robert Bell, Chris Volinsky In IEEE Computer, Vol. 42, No. 8. (07 August 2009), pp. 30-37. 
  Takács, G, Pilászy, I., Németh, B. and Tikk, D. (2009). Scalable Collaborative Filtering Approaches for Large Recommender Systems. Journal of Machine Learning Research, 10, 623-656.
  

• Bias stochastic gradient descent (Bias-SGD)

  Y. Koren. Factorization Meets the Neighborhood: a Multifaceted Collaborative Filtering Model. ACM SIGKDD 2008. Equation (5).

• SVD++

  Y. Koren. Factorization Meets the Neighborhood: a Multifaceted Collaborative Filtering Model. ACM SIGKDD 2008. 

• Weighted-ALS

  Collaborative Filtering for Implicit Feedback Datasets Hu, Y.; Koren, Y.; Volinsky, C. IEEE International Conference on Data Mining (ICDM 2008), IEEE (2008). 

• Sparse-ALS

  Xi Chen, Yanjun Qi, Bing Bai, Qihang Lin and Jaime Carbonell. Sparse Latent Semantic Analysis. In SIAM International Conference on Data Mining (SDM), 2011. 
  D. Needell, J. A. Tropp CoSaMP: Iterative signal recovery from incomplete and inaccurate samples Applied and Computational Harmonic Analysis, Vol. 26, No. 3. (17 Apr 2008), pp. 301-321. 

• NMF
  

  Lee, D..D., and Seung, H.S., (2001), 'Algorithms for Non-negative Matrix
  Factorization', Adv. Neural Info. Proc. Syst. 13, 556-562.

  SVD (Restarted Lanczos & One sided Lanczos)

• V. Hern´andez, J. E. Rom´an and A. Tom´as. STR-8: Restarted Lanczos Bidiagonalization for the SVD in SLEPc. 

  
  

使用GraphChi的好处在于，只需要用单台多核电脑就可以处理庞大的模型。这是因为模型数据可以不必全部加载的内存中，而是在硬盘中读写。运行时最多占用多少内存，也是可以配置的。

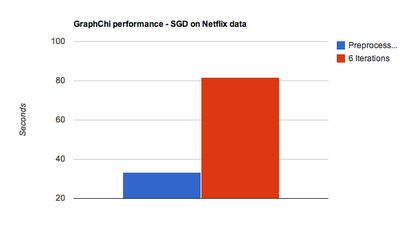
上图展示了GraphChi的性能。这是在全量的Netflix数据集上做SGD矩阵分解，迭代6次使用的时间。Netflix拥有大约1亿个评分信息，待分解的矩阵是48万用户 乘以 1万个电影，分解时latent factor的取值是D=20。测试机器是多核的，开启了8个线程，内存占用被限制在800M。迭代6轮的时间大约是80秒。

The input to GraphChi ALS/SGD/bias-SGD is the sparse matrix A in sparse matrix market format. The output are two matrices U and V s.t. A ~= U*V'  and both U and V have  a lower dimension D.

Let's start with an example:

1) Download graphchi from mercurial using the instructions  here .

2) Change directory to graphchi
     cd graphchi

3) Download Eigen and put the header files inside the ./src directory
     wget http://bitbucket.org/eigen/eigen/get/3.1.1.tar.bz2
  tar -xjf 3.1.1.tar.bz2
  mv eigen-eigen-43d9075b23ef/Eigen ./src

4) Compile using
     make cf

5a) For ALS/SGD/bias-SGD/SVD++/SVD Download Netflix synthetic sample file. The input is in sparse matrix market format .
     wget http://www.select.cs.cmu.edu/code/graphlab/datasets/smallnetflix_mm 
  wget http://www.select.cs.cmu.edu/code/graphlab/datasets/smallnetflix_mme 

5b) For WALS Download netflix sample file including time:

  wget http://www.select.cs.cmu.edu/code/graphlab/datasets/time_smallnetflix
  wget http://www.select.cs.cmu.edu/code/graphlab/datasets/time_smallnetflixe

6a) Run ALS on the Netflix example:
      ./bin/als --training= smallnetflix_mm  --validation=smallnetflix_mme --lambda=0.065  --minval=1 --maxval=5 --max_iter=6 --quiet=1

   At the first time, the input file will be preprocessed into an efficient binary representation on disk and then 6 ALS iterations will be run. 

6b) Run SGD on the Netflix example:
   ./bin/sgd --training= smallnetflix_mm  --validation=smallnetflix_mme --sgd_lambda=1e-4 -----sgd_gamma=1e-4 --minval=1 --maxval=5 --max_iter=6 --quiet=1

6c) Run bias-SGD on the Netflix example:
   ./bin/biassgd --training= smallnetflix_mm  --validation=smallnetflix_mme --biassgd_lambda=1e-4 --biassgd_gamma=1e-4  --minval=1 --maxval=5 --max_iter=6 --quiet=1

6d) Run SVD++ on Netflix example:

   ./bin/svdpp --training=smallnetflix_mm --validation=smallnetflix_mme --biassgd_lambda=1e-4 --biassgd_gamma=1e-4  --minval=1 --maxval=5 --max_iter=6 --quiet=1

6e) Run weighted-ALS on the Netflix time example:
   ./bin/als --training=time_smallnetflix --validation=smallnetflix_mme --lambda=0.065  --minval=1 --maxval=5 --max_iter=6 --quiet=1

6f) Run NMF on the reverse Netflix example:

./bin/nmf --training=reverse_netflix.mm --minval=1 --maxval=5 --max_iter=20 --quiet=1

6g) Run one sided SVD on the Netflix example:
./bin/svd_onesided --training= smallnetflix_mm  --nsv=3 --nv=10 --max_iter=1 --quiet=1 --tol=1e-1

7) View the output.

For ALS, SGD, bias-SGD, WALS, SVD++ and NMF

Two files are created:  filename_U.mm and filename_V.mm
    The files store the matrices U and V in  sparse matrix market format .
     head smallnetflix_mm_U.mm

%%MatrixMarket matrix array real general
95526 5
0.693370
1.740420
0.947675
1.328987
1.150084
1.399164
1.292951
0.300416

For bias-SGD, SVD++

Additional three files are created: filename_U_bias.mm, filename_V_bias.mm and filename_global_mean.mm. Bias files include the bias for each user (U) and item (V).
The global mean file includes the global mean of the rating.

For SVD

For each singular vector a file named filename.U.XX is created where XX is the number of the singular vector. The same with filename.V.XX. Additionally a singular value files is also saved.

Load output in Matlab (optional)

a) download the script  mmread.m.

b)  # matlab

    >> A=mmread('smallnetflix_mm');

    >> U=mmread('smallnetflix_mm_U.mm');

    >> V=mmread('smallnetflix_mm_V.mm');

    >> whos

  Name          Size                  Bytes  Class     Attributes

  A         95526x3561             52799104  double    sparse    

  U         95526X5                3821040   double              

  V         3561X5                 142480    double          

c) compute prediction for user 8 movie 12:
   >> U(8,:)*V(12,:)'

d) compute approximation error     

      >> norm(A-U*V') % may be slow... depending on problem size

Command line options:

Common options:

--training - the training input file
--validation - the validation input file (optional). Validation is data with known ratings which not used for training.
--test - the test input file (optional).

--minval - min allowed rating (optional). It is highly recommended to set this value since it improves prediction accuracy.
--maxval - max allowed rating (optional). It is highly recommended to set this value since it improves prediction accuracy.
--max_iter  - number of iterations to run
--quiet - 1 run with less traces.
D - width of the factorized matrix. Default is 20. To change it you need to edit the file toolkits/collaborative_filtering/XXX.hpp (where XXX is the algorithm name), and change the macro #define D to some other value and recompile.

ALS:

--lambda - regularization parameter (optional, default value 0.065)

SGD:

--lambda - gradient step size (optional). Default value 1e-3.
--gamma - regularization (optional). Default value 1e-3.
--sgd_step_dec - multiplicative step decrement (optional). Default is 0.9.

bias-SGD:

--biassgd_lambda - gradient step size (optional). Default value 1e-3.
--biassgd_gamma - regularization (optional). Default value 1e-3.
--biassgd_step_dec - multiplicative gradient step decrement (optional). Default is 0.9.

SVD++

- -svdpp_item_bias_step, --svdpp_user_bias_step, --svdpp_user_factor_step, --svdpp_user_factor2_step - gradient step size (optional). Default value 1e-4.
--svdpp_item_bias_reg, --svdpp_user_bias_reg, --svdpp_user_factor_reg, --svdpp_user_factor2_reg - regularization (optional). Default value 1e-4.
--svdpp_step_dec - multiplicative gradient step decrement (optional). Default is 0.9.

Weighted-ALS

Note: for weighted-ALS, the input file has 4 columns:

[user] [item] [time] [rating]. See example file in section 5b).

--lambda - regularization

Sparse-ALS

--lambda - regularization

--user_sparsity - defines sparsity of each of the user factors. Value should be in the range [0.5,1)

--movie_sparsity - defines sparsity of each of the movie factors. Value should be in the range [0.5,1)

--algorithm - sparsity pattern. There are three run modes:

                           SPARSE_USR_FACTOR = 1

                           SPARSE_ITM_FACTOR = 2

                           SPARSE_BOTH_FACTORS = 3

Example running sparse-ALS:

bickson@thrust:~/graphchi$ ./bin/sparse_als.cpp --training=smallnetflix_mm --user_sparsity=0.8 --movie_sparsity=0.8 --algorithm=3 --quiet=1 --max_iter=15

WARNING:  sparse_als.cpp(main:202): GraphChi Collaborative filtering library is written by Danny Bickson (c). Send any  comments or bug reports to [email protected] 

[training] => [smallnetflix_mm]

[user_sparsity] => [0.8]

[movie_sparsity] => [0.8]

[algorithm] => [3]

[quiet] => [1]

[max_iter] => [15]

  0) Training RMSE:    1.11754  Validation RMSE:    3.82345

  1) Training RMSE:    3.75712  Validation RMSE:      3.241

  2) Training RMSE:    3.22943  Validation RMSE:    2.03961

  3) Training RMSE:    2.10314  Validation RMSE:    2.88369

  4) Training RMSE:    2.70826  Validation RMSE:    3.00748

  5) Training RMSE:    2.70374  Validation RMSE:    3.16669

  6) Training RMSE:    3.03717  Validation RMSE:     3.3131

  7) Training RMSE:    3.18988  Validation RMSE:    2.83234

  8) Training RMSE:    2.82192  Validation RMSE:    2.68066

  9) Training RMSE:    2.29236  Validation RMSE:    1.94994

 10) Training RMSE:    1.58655  Validation RMSE:    1.08408

 11) Training RMSE:     1.0062  Validation RMSE:    1.22961

 12) Training RMSE:    1.05143  Validation RMSE:     1.0448

 13) Training RMSE:   0.929382  Validation RMSE:    1.00319

 14) Training RMSE:   0.920154  Validation RMSE:   0.996426

NMF

NMF Has no special command line arguments.

SVD

SVD is implemented using therestarted lanczos algorithm.
The input is a sparse matrix market format input file.
The output are 3 files: one file containing the singular values, and two dense matrix market format files containing the matrices U and V.

Note: for larger models, it is advised to usesvd_onesided since it significantly saved memory.

Here is an example Matrix Market input file for the matrix A2:

<235|0>bickson@bigbro6:~/ygraphlab/graphlabapi/debug/toolkits/parsers$ cat A2
%%MatrixMarket matrix coordinate real general
3 4 12
1 1  0.8147236863931789
1 2  0.9133758561390194
1 3  0.2784982188670484
1 4  0.9648885351992765
2 1  0.9057919370756192
2 2  0.6323592462254095
2 3  0.5468815192049838
2 4  0.1576130816775483
3 1  0.1269868162935061
3 2  0.09754040499940952
3 3  0.9575068354342976
3 4  0.9705927817606157


Here is an for running SVD :

bickson@thrust:~/graphchi$ ./bin/svd --training=A2 --nsv=4 --nv=4 --max_iter=4 --quiet=1WARNING: svd.cpp(main:329): GraphChi Collaborative filtering library is written by Danny Bickson (c). Send any comments or bug reports to [email protected] [training] => [A2][nsv] => [4][nv] => [4][max_iter] => [4][quiet] => [1]Load matrix set status to tol Number of computed signular values 4Singular value 0 2.16097 Error estimate: 2.35435e-16Singular value 1 0.97902 Error estimate: 1.06832e-15Singular value 2 0.554159 Error estimate: 1.56173e-15Singular value 3 9.2673e-65 Error estimate: 6.51074e-16Lanczos finished 7.68793

Command line arguments

Basic configuration	--training	Input file name. Note that even for the binary format, the header of the matrix market file (first 2-3 lines) should be present, at the same folder where the .nodes, .edges, and .weights files are found.
	--nv	Number of inner steps of each iterations. Typically the number should be greater than the number of singular values you look for.
	--nsv	Number of singular values requested. Should be typically less than --nv
	--ortho_repeats	Number of repeats on the orthogonalization step. Default is 1 (no repeats). Increase this number for higher accuracy but slower execution. Maximal allowed values is 3.
	--max_iter	Number of allowed restarts. The minimum is 2= no restart.
	--save_vectors=true	Save the factorized matrices U and V to file.
	--tol	Convergence threshold. For large matrices set this number set this number higher (for example 1e-1, while for small matrices you can set it to 1e-16). As smaller the convergence threshold execution is slower.

Understanding the error measure

Following Slepc, the error measure is computed by a combination of:
sqrt( ||Av_i - sigma(i) u_i ||_2^2 + ||A^Tu_i - sigma(i) V_i ||_2^2 ) / sigma(i)


Namely, the deviation of the approximation sigma(i) u_i  from Av_i , and vice versa.

Scalability

Currently the code was tested with up to 3.5 billion non-zeros on a 24 core machine. Each Lanczos iteration takes about 30 seconds.

Difference to Mahout

Mahout SVD solver is implemented using the same Lanczos algorithm. However, there are several differences
1) In Mahout there are no restarts, so quality of the solution deteriorates very rapidly, after 5-10 iterations the solution is no longer accurate. Running without restarts can be done using our solution with the --max_iter=2 flag.
2) In Mahout there is a single orthonornalization step in each iteration while in our implementation there are two (after computation of u_i and after v_i ).
3) In Mahout there is no error estimation while we provide for each singular value the approximated error.
4) Our solution is typically x100 times faster than Mahout.

Common erros and their meaning

File not found error:

bickson@thrust:~/graphchi$ ./bin/example_apps/matrix_factorization/als_vertices_inmem file smallnetflix_mm 
INFO:     sharder.hpp(start_preprocessing:164): Started preprocessing: smallnetflix_mm --> smallnetflix_mm.4B.bin.tmp
ERROR:    als.hpp(convert_matrixmarket_for_ALS:153): Could not open file: smallnetflix_mm, error: No such file or directory

Solution:

Input file is not found, repeat step 5 and verify the file is in the right folder

Environment variable error:

bickson@thrust:~/graphchi/bin/example_apps/matrix_factorization$ ./als_vertices_inmem 

ERROR: Could not read configuration file: conf/graphchi.local.cnf

Please define environment variable GRAPHCHI_ROOT or run the program from that directory.

Solution:

export GRAPHCHI_ROOT=/path/to/graphchi/folder/