虹膜识别（三）：Hough变换检测内圆边缘

前面我们已经得到了hough变换的基础条件，那就是有一个很好的用于检测的二值边缘图像如下所示：

 

至此我们才能运用hough变换。

Hough变换是一类广泛用于检测各种规则图形用的，像直线、圆、椭圆等等，不同的就是检测的规律不同。Hough变换的原理网上多得是，像http://blog.163.com/yuyang_tech/blog/static/21605008320130233343990/   我当初也是百度上查的，就不详细说原理了（可能也说不明白），直接上程序了。。

function mean_circle = hough_circle(BW,step_r,step_angle,r_min,r_max,p)
%------------------------------算法概述-----------------------------
% 该算法通过a = x-r*cos(angle)，b = y-r*sin(angle)将圆图像中的边缘点
% 映射到参数空间(a,b,r)中，由于是数字图像且采取极坐标，angle和r都取
% 一定的范围和步长，这样通过两重循环（angle循环和r循环）即可将原图像
% 空间的点映射到参数空间中，再在参数空间（即一个由许多小立方体组成的
% 大立方体)中寻找圆心，然后求出半径坐标。
%-------------------------------------------------------------------
%------------------------------输入参数-----------------------------
% BW:二值图像；
% step_r:检测的圆半径步长  
% step_angle:角度步长，单位为弧度   :各度计算  1° = 0.0174 
%                                              2° = 0.035  
%                                              3° = 0.0524
%                                              4° = 0.0698
%                                              5° = 0.0872
% r_min:最小圆半径
% r_max:最大圆半径
% p:以p*hough_space的最大值为阈值，p取0，1之间的数
%-------------------------------------------------------------------
%          --------对半径的大小范围规定问题--------
%         ------ 实验中发现：外轮廓的半径范围在220~260之间   
%                           内轮廓的半径范围 60~80之间   
%    Note：：  &&&&&&&&&&&当图像改变时半径范围需要改变&&&&&&&&&&&&
%    question： 半径的范围差超过50将会显示内存不足，注意方案办法
%------------------------------输出参数-----------------------------
% hough_space:参数空间，h(a,b,r)表示圆心在(a,b)半径为r的圆上的点数
% hough_circl:二值图像，检测到的圆
% para:检测到的所有圆的圆心、半径
% mean_circle ： 返回检测到的圆的平均位置及大小
%-------------------------------------------------------------------

[m,n] = size(BW);  %取大小
size_r = round((r_max-r_min)/step_r)+1; %半径增加，循环次数
size_angle = round(2*pi/step_angle);    %角度增加，循环次数
hough_space = zeros(m,n,size_r);       %hough空间
[rows,cols] = find(BW);%把要检测的点存起来，只有白色（边缘）点需要变换
ecount = size(rows);   %检测的点的个数

tic    %%%% 计时开始位置 
% Hough变换
% 将图像空间(x,y)对应到参数空间(a,b,r)
% a = x-r*cos(angle)
% b = y-r*sin(angle)
for i=1:ecount      %点个数循环
    for r=1:size_r   %单个点在所有半径空间内检测
        for k=1:size_angle  %单个点在半径一定的所在圆内检测
            a = round(rows(i)-(r_min+(r-1)*step_r)*cos(k*step_angle));
            b = round(cols(i)-(r_min+(r-1)*step_r)*sin(k*step_angle));
            if(a>0&a<=m&b>0&b<=n)   %对应到某个圆上，记录之
                hough_space(a,b,r) = hough_space(a,b,r)+1;
            end
        end
    end
end
% 搜索超过阈值的聚集点
max_para = max(max(max(hough_space)));%找到最大值所在圆参数
index = find(hough_space>=max_para*p);%索引在一定范围内的圆参数
length = size(index);
toc  %%%% 计时结束位置，通过计时观察运行效率，hough变换的一大缺点就是耗时

% 将索引结果转换为对应的行列（圆心）和半径大小
% 理解三维矩阵在内存中的存储方式可以理解公式的原理
for k=1:length
    par3 = floor(index(k)/(m*n))+1;
    par2 = floor((index(k)-(par3-1)*(m*n))/m)+1;%转换为圆心的y值
    par1 = index(k)-(par3-1)*(m*n)-(par2-1)*m;%转换为圆心的x值
    par3 = r_min+(par3-1)*step_r; %转化为圆的半径
    %储存在一起
    para(:,k) = [par1,par2,par3]';
end
% 为提高准确性，求取一个大致的平均位置（而不是直接采用的最大值）
mean_circle = round(mean(para')');

导入二值图后，设置一定步长参数运行，例如：mean_circle = hough_circle(J,2,0.0524,60,80,0.9);

这样就得到了内圆的参数值，运行结果如下：

运行时间：Elapsed time is 0.409292 seconds.

>> mean_circle

mean_circle =

   326
   331
    66

可以看到圆心坐标和半径参数，在坐标中画出这个圆，编写画圆函数如下：

function plot_circle(circle_num)
%------------------------------输入参数-----------------------------
%给定圆的参数画出一个圆形
%圆参数   circle_num:
%                   circle_num(1) : 圆心横坐标
%                   circle_num(2) ：圆心纵坐标
%                   circle_num(3) ：圆的半径
%-------------------------------------------------------------------
radius_y = circle_num(1);
radius_x = circle_num(2);
radius = circle_num(3);

alpha=0:pi/20:2*pi;%角度[0,2*pi]
R=radius;           %半径
%规整到图的对应位置
x=R*cos(alpha)+radius_x;   
y=R*sin(alpha)+radius_y;
hold on,plot(x,y)

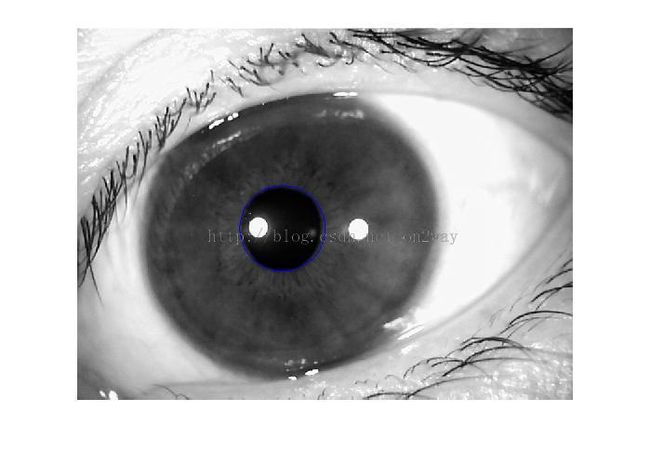
最后把圆的参数和以前的那个图画在一起如下：

 

画成这样应该很准了吧，基本上贴近内圆了，再把它画在原图中可以看到：

 

至此内圆的检测就完成了，当然其中有很多参数需要调整的，并且每一副图对应的参数不太一样，实验还需要看效果调整。