Treap(树堆)

 

Treap(树堆)

分类： algorithm 2013-09-30 10:13  57人阅读  评论(0)  收藏  举报

treap

目录(?)[+]

    Treap，就是有另一个随机数满足堆的性质的二叉搜索树，其结构相当于以随机顺序插入的二叉搜索树。其基本操作的期望复杂度为O(log n)。

    其特点是实现简单，效率高于伸展树并且支持大部分基本功能，性价比很高。

 前言

    我们可以看到，如果一个二叉搜索树节点插入的顺序是随机的，这样我们得到的二叉搜索树大多数情况下是平衡的，即使存在一些极端情况，但是这种情况发生的概率很小，所以我们可以这样建立一棵二叉搜索树，而不必要像AVL那样旋转，可以证明随机顺序建立的二叉搜索树在期望高度是O(log n)，但是某些时候我们并不能得知所有的待插入节点，打乱以后再插入。所以我们需要一种规则来实现这种想法，并且不必要所有节点。也就是说节点是顺序输入的，我们实现这一点可以用Treap。

介绍

    Treap=Tree+Heap。Treap本身是一棵二叉搜索树，它的左子树和右子树也分别是一个Treap，和一般的二叉搜索树不同的是，Treap记录一个额外的数据，就是优先级。Treap在以关键码构成二叉搜索树的同时，还按优先级来满足堆的性质(在这里我们假设节点的优先级小于该节点的孩子的优先级)。但是这里要注意的是Treap和二叉堆有一点不同，就是二叉堆必须是完全二叉树，而Treap可以并不一定是。（网友注：这些图来自算法导论）

操作

Treap维护堆性质的方法用到了旋转，这里先简单地介绍一下。Treap只需要两种旋转，这样编程复杂度比Splay等就要小一些，这正是Treap的特色之一。

旋转是这样的： 

插入

给节点随机分配一个优先级，先和二叉搜索树的插入一样，先把要插入的点插入到一个叶子上，然后跟维护堆一样，如果当前节点的优先级比根小就旋转，如果当前节点是根的左儿子就右旋如果当前节点是根的右儿子就左旋。 即左旋能使根节点转移到左边，右旋能使根节点转移到右边。

我们如果把插入写成递归形式的话，只需要在递归调用完成后判断是否满足堆性质，如果不满足就旋转，实现非常容易。（这里我lsj有点小疑问：怎么保证旋转后的节点的优先级比根节点大，是不是要向上溯继续调整？本文给得程序没有上溯，何解？）

由于旋转是O(1)的，最多进行h次(h是树的高度),插入的复杂度是O(h)的，在期望情况下h=O(log n)，所以它的期望复杂度是O(log n)。

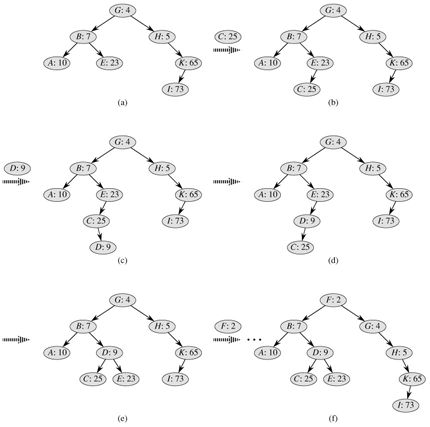  "如果当前节点的优先级比根小就旋转，如果当前节点是根的左儿子就右旋如果当前节点是根的右儿子就左旋。"

删除

有了旋转的操作之后，Treap的删除比二叉搜索树还要简单。因为Treap满足堆性质，所以我们只需要把要删除的节点旋转到叶节点上，然后直接删除就可以了。具体的方法就是每次找到优先级最小的儿子，向与其相反的方向旋转，直到那个节点被旋转到了叶节点，然后直接删除。

删除最多进行O(h)次旋转，期望复杂度是O(log n)。。

查找

和一般的二叉搜索树一样，但是由于Treap的随机化结构，可以证明Treap中查找的期望复杂度是O(log n)。

分离

要把一个Treap按大小分成两个Treap，只要在需要分开的位置加一个虚拟节点，然后旋至根节点删除，左右两个子树就是得出的两个Treap了。根据二叉搜索树的性质，这时左子树的所有节点都小于右子树的节点。

时间相当于一次插入操作的复杂度，也就是O(log n)。

合并

合并是指把两个平衡树（或者其他的有序表）合并成一个平衡树（有序表），其中第一个树（表）的所有节点都必须小于或等于第二个树（表）中的所有节点，这也是上面的分离操作的结果所满足的条件。

Treap的合并操作的过程和分离相反，只要加一个虚拟的根，把两棵树分别作为左右子树，然后把根删除就可以了。

时间复杂度和删除一样，也是期望O(log n)。

参考程序

Treap_Pascal

Treap_C

Treap_C++

算法分析

首先我们注意到二叉搜索树有一个特性，就是每个子树的形态在优先级唯一确定的情况下都是唯一的，不受其他因素影响，也就是说，左子树的形态与树中大于根节点的值无关，右子树亦然。

这是因为Treap满足堆的性质，Treap的根节点是优先级最小的那个节点，考虑它的左子树，树根也是子树里面最小的一点，右子树亦然。所以Treap相当于先把所有节点按照优先级排序，然后插入，实质上就相当于以随机顺序建立的二叉搜索树，只不过它并不需要一次读入所有数据，可以一个一个地插入。而当这个随机顺序确定的时候，这个树是唯一的。

因此在给定优先级的情况下，只要是用符合要求的操作，通过任何方式得出的Treap都是一样的，所以不改变优先级的情况下，特殊的操作不会造成Treap结构的退化。而改变优先级可能会使Treap变得不够随机以致退化。

证明随机建立二叉搜索树的E[h]=O(log n)大家可以参见CLRS P265 12.4 Randomly built binary search trees，这里略去。

如果有E[h]=O(log n)我们就证明了，Treap插入的期望复杂度是O(log n)。

Treap的其它操作的期望复杂度同样是O(log n)。

评价

与其他结构的比较

• AVL树（基于长度保持平衡的二叉查找树）
• 伸展树（Splay Tree，一种基于查找次序优化的二叉查找树，适用于查询操作比较集中的查询集合）
• 线段树（可以保存线段，往往用于统计、图形等题目）
• 红黑树(红黑树编程更理性一些，但编程复杂度更高)
• SBT (SBT比TREAP的速度更快，但编程复杂度更高)

实现代码：

 #include <iostream>
 #include <ctime>
 #define MAX 100

 using namespace std;

 typedef struct
 {
     int l,r,key,fix;
 }node;

 class treap
 {
 public:
     node p[MAX];
     int size,root;
     treap()
     {
         srand(time(0));
         size=-1;
         root=-1;
     }

     void rot_l(int &x)  //看上面的图解
     {
         int y=p[x].r;
         p[x].r=p[y].l;
         p[y].l=x;
         x=y;
     }

     void rot_r(int &x) //看上面的图解
     {
         int y=p[x].l;
         p[x].l=p[y].r;
         p[y].r=x;
         x=y;
     }

     void insert(int &k,int tkey)
     {
         if (k==-1) //根节点为空，空树
         {
             k=++size;
             p[k].l=p[k].r=-1;//左右子树置为空
             p[k].key=tkey;//保存关键字
             p[k].fix=rand();//生产一个随机的优先级
         }
         else
             if (tkey<p[k].key)  //按照二叉查找树的规律去插入
             {
                 insert(p[k].l,tkey);
                 if (p[ p[k].l ].fix>p[k].fix) //但是插完不满足条件要进行旋转
                     rot_r(k);
             }
             else
             {
                 insert(p[k].r,tkey);
                 if (p[ p[k].r ].fix>p[k].fix)
                     rot_l(k);
             }

     }

     void remove(int &k,int tkey)  //删除节点
     {
         if (k==-1) return;
         if (tkey<p[k].key)  //按照而叉查找树的规律去查找
             remove(p[k].l,tkey);
         else if (tkey>p[k].key)
             remove(p[k].r,tkey);
         else
         {
             if (p[k].l==-1 && p[k].r==-1) //被删除的是叶子节点，直接删除
                 k=-1;
             else if (p[k].l==-1)  //被删除的左孩子节点为空
                 k=p[k].r;
             else if (p[k].r==-1) //被删除的有孩子节点为空
                 k=p[k].l;
             else
                 if (p[ p[k].l ].fix < p[ p[k].r ].fix)  //选择孩子节点小的方向旋转
                 {
                     rot_l(k);
                     remove(p[k].l,tkey);
                 }
                 else
                 {
                     rot_r(k);
                     remove(p[k].r,tkey);
                 }
         }
     }

     void print(int k)  //中序遍历
     {
         if (p[k].l!=-1)
             print(p[k].l);
         cout << p[k].key << " : " << p[k].fix << endl;
         if (p[k].r!=-1)
             print(p[k].r);
     }
 };

 treap T;

 int main()
 {

     int i;
     for (i=8;i>=1;i--)
         T.insert(T.root,i);
         cout<<"插入节点之后："<<endl;
     T.print(T.root);
     for (i=3;i>=1;i--)
     {
         cout << "删除key为"<<i<<"的节点："<<endl;
         T.remove(T.root,i);
         T.print(T.root);
     }
     system("pause");
     return 0;
 }