递归优化 POJ1579 记忆化搜索 剪枝 去掉重复计算

 

         题意描述很简单，阅读无障碍。当然直接递归，会有很多重复计算，效率必然很低。优化势在必行，关键如何优化。

         首先想到的当然是动态规划。DP的优势就在于打表，从而减少重复计算。况且，很少有题目会把状态转换方程赤裸裸的给出来。这里的难点在于：不知道怎样由初始状态，根据状态方程，一步一步往下计算，直至问题求解。

状态方程：

（1）if a <= 0 or b <= 0 or c <= 0, then w(a, b, c) = 1                     

（2）if a > 20 or b > 20 or c > 20, then w(a, b, c) =  w(20, 20, 20)          

（3）if a < b and b < c, then w(a, b, c) = w(a, b, c-1) + w(a, b-1, c-1) - w(a, b-1, c)

（4）otherwise，w(a, b, c) = w(a-1, b, c) + w(a-1, b-1, c) + w(a-1, b, c-1) - w(a-1, b-1, c-1)

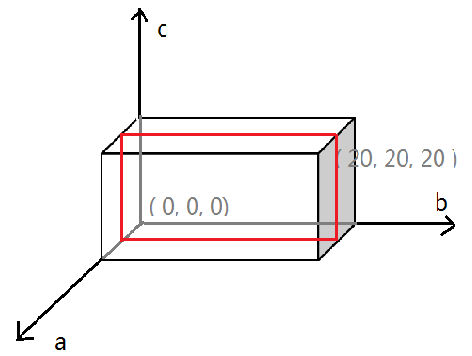
        如图所示：首先，由状态方程（1）（2），可以把要求的点限定在图中的长方体内。初始时，点( 0, 0, 0 )可知，由状态方程（1）可知，ab平面、ac平面、bc平面内的点都可知。然后，W( 1, X, X )根据状态方程（4）可以转换为W( 0, X, X )。同理W( 2, X, X )à W( 1, X, X )。这样，平行于bc平面的切面（图中红线所示， a为int，最多有20个）依次可知。在同一个切面内，如果满足条件，则可使用状态方程（3）

        具体编程实现时，可以用一个全局变量dp[a][b][c], 这样即使在不同的测试用例之间，也可以避免重复计算。 

        除了DP，也可以直接用递归。只不过为了避免重复，也需要打表。这样在递归调用前，可以先查表，如果已经计算过，则直接返回。

 

#include <iostream>
using namespace std;

//***********************常量定义*****************************

const int NUM = 22;


//*********************自定义数据结构*************************




//********************题目描述中的变量************************





//**********************算法中的变量**************************

int dp[NUM][NUM][NUM];
bool visit[NUM][NUM][NUM];


//***********************算法实现*****************************

//记忆化搜索 递归形式的实现
int RecSolve( int a, int b, int c )
{
	if( a<=0 || b<=0 || c<=0 )
	{
		return 1;
	}
	if( a>20 || b>20 || c>20 )
	{
		return RecSolve( 20, 20, 20 );
	}
	
	//先查找，看以前是否计算过
	if( visit[a][b][c] )
	{
		return dp[a][b][c];
	}

	visit[a][b][c] = true;
	if( a<b && b<c )
	{		
		return dp[a][b][c] = RecSolve(a, b, c-1) + RecSolve(a, b-1, c-1) - RecSolve(a, b-1, c); 
	}
	else
	{		
		return dp[a][b][c] = RecSolve(a-1, b, c) + RecSolve(a-1, b-1, c) + RecSolve(a-1, b, c-1) - RecSolve(a-1, b-1, c-1); 
	}
}

//DP实现
int DPSolve( int a, int b, int c )
{	
	if( a<0 || b<0 || c<0 )
	{
		a = b = c = 0;
	}
	if( a>20 || b>20 || c>20 )
	{
		a = b = c = 20;
	}

    //a ,b ,c可能为负，必须放在if( a<0 || b<0 || c<0 )之后
	if( visit[a][b][c] )
	{
		return dp[a][b][c];
	}	

	int x, y, z;
	for( z=0; z<=a; z++ )
	{
		for( x=0; x<=b; x++ )
		{
			for( y=0; y<=c; y++ )
			{
				if( z==0 || x==0 || y==0 )
				{
					dp[z][x][y] = 1;
				}
				else if( z<x && x<y )
				{
					dp[z][x][y] = dp[z][x][y-1] + dp[z][x-1][y-1] - dp[z][x-1][y];
				}
				else
				{
					dp[z][x][y] = dp[z-1][x][y] + dp[z-1][x-1][y] + dp[z-1][x][y-1] - dp[z-1][x-1][y-1];			
				}
				//visit是全局变量
				//如果已经计算过，则设置标记				
				visit[z][x][y] = true;
			}
		}
	}	
	return dp[a][b][c];		
}

//************************main函数****************************

int main()
{
	freopen( "in.txt", "r", stdin );	
	memset( dp, 0, sizeof(dp) );
	memset( visit, false, sizeof(visit) );
	
	int a, b, c;	
	while( cin >> a >> b >> c, !( a == -1 && b == -1 && c == -1 ) )
	{
		int ans = RecSolve( a, b, c );		
		cout << "w(" << a << ", " << b << ", " << c << ") = " << ans << endl;
	}

	return 0;
}