树学习 ---------树堆（Treap Tree）

树堆，在数据结构中也称Treap，是指有一个随机附加域满足堆的性质的二叉搜索树，其结构相当于以随机数据插入的二叉搜索树。

其基本操作的期望时间复杂度为O(logn)。相对于其他的平衡二叉搜索树，Treap的特点是实现简单，且能基本实现随机平衡的结构。

这个堆树的结构和数据结构中的堆类似，可以排序并且：

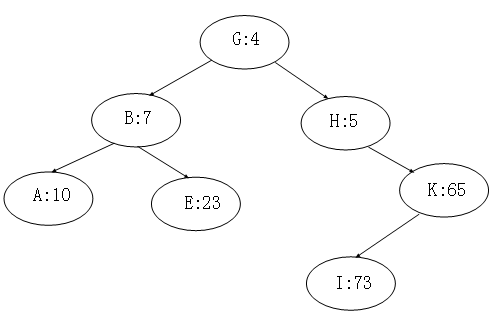
显示一个例子，通常树内的每个结点x都有一个关键字值key[x]，另外，还要为结点分配priority[x]，它是一个独立选取的随机数。
假设所有的优先级是不同的，所有的关键字也是不同的。treap的结点排列成让关键字遵循二叉查找树性质，并且优先级遵循最小堆顺序性质：
1.如果v是u的左孩子，则key[v] < key[u].
2.如果v是u的右孩子，则key[v] > key[u].
3.如果v是u的孩子，则priority[u] > priority[u].
这两个性质的结合就是为什么这种树被称为“treap”的原因，因为它同时具有二叉查找树和堆的特征。

用以下方式考虑treap会有帮助。假设插入关联关键字的结点x1，x2，...，xn到一棵treap内。结果的treap是将这些结点以它们的优先级(随机选取)的顺序插入一棵正常的二叉查找树形成的，亦即priority[xi] < priority[xj]表示xi在xj之前被插入。
在算法导论的12.4节中，其证明了随机构造的二叉查找树的期望高度为O(lgn)，因而treap的期望高度亦是O(lgn)。

Treap=Tree+Heap。Treap本身是一棵二叉搜索树，它的左子树和右子树也分别是一个Treap，和一般的二叉搜索树不同的是，Treap纪录一个额外的数据，就是优先级。Treap在以关键码构成二叉搜索树的同时，还满足堆的性质。Treap维护堆性质的方法用到了旋转，只需要两种旋转，编程复杂度比Splay要小一些。

插入

给节点随机分配一个优先级，先和二叉搜索树的插入一样，先把要插入的点插入到一个叶子上，然后跟维护堆一样，如果当前节点的优先级比根大就旋转，如果当前节点是根的左儿子就右旋如果当前节点是根的右儿子就左旋。

由于旋转是的，最多进行h次（h是树的高度），插入的复杂度是的O(h)，在期望情况下h = O(log n)，所以它的期望复杂度是O(log n)。

删除

因为Treap满足堆性质，所以只需要把要删除的节点旋转到叶节点上，然后直接删除就可以了。具体的方法就是每次找到优先级最大的儿子，向与其相反的方向旋转，直到那个节点被旋转到了叶节点，然后直接删除。

删除最多进行O(H)次旋转，期望复杂度是o(log n)。

查找

和一般的二叉搜索树一样，但是由于Treap的随机化结构，Treap中查找的期望复杂度是O(log n)

与其他结构的比较

• AVL树（基于长度保持平衡的二叉查找树）
• 伸展树（Splay Tree，一种基于查找次序优化的二叉查找树，适用于查询操作比较集中的查询集合）
• 线段树（可以保存线段，往往用于统计、图形等题目）
• 红黑树(红黑树编程更理性一些，但编程复杂度更高)
• SBT (SBT比TREAP的速度更快，但编程复杂度更高)

C++代码：

#include <iostream>  

#include <cstdio>

#include <ctime>  
#define MAX 100  
  
using namespace std;  
  
typedef struct  
{  
    int l,r,key,fix;  
}node;  
  
class treap  
{  
public:  
    node p[MAX];  
    int size,root;  
    treap()  
    {  
        srand(time(0));  
        size=-1;  
        root=-1;  
    }  
  
    void rot_l(int &x)  //看上面的图解  
    {  
        int y=p[x].r;  
        p[x].r=p[y].l;  
        p[y].l=x;  
        x=y;  
    }  
  
    void rot_r(int &x) //看上面的图解  
    {  
        int y=p[x].l;  
        p[x].l=p[y].r;  
        p[y].r=x;  
        x=y;  
    }  
  
    void insert(int &k,int tkey)  
    {  
        if (k==-1) //根节点为空，空树  
        {  
            k=++size;  
            p[k].l=p[k].r=-1;//左右子树置为空  
            p[k].key=tkey;//保存关键字  
            p[k].fix=rand();//生产一个随机的优先级  
        }  
        else  
            if (tkey<p[k].key)  //按照二叉查找树的规律去插入  
            {  
                insert(p[k].l,tkey);  
                if (p[ p[k].l ].fix>p[k].fix) //但是插完不满足条件要进行旋转  
                    rot_r(k);  
            }  
            else  
            {  
                insert(p[k].r,tkey);  
                if (p[ p[k].r ].fix>p[k].fix)  
                    rot_l(k);  
            }  
  
    }  
  
    void remove(int &k,int tkey)  //删除节点  
    {  
        if (k==-1) return;  
        if (tkey<p[k].key)  //按照而叉查找树的规律去查找  
            remove(p[k].l,tkey);  
        else if (tkey>p[k].key)  
            remove(p[k].r,tkey);  
        else  
        {  
            if (p[k].l==-1 && p[k].r==-1) //被删除的是叶子节点，直接删除  
                k=-1;  
            else if (p[k].l==-1)  //被删除的左孩子节点为空  
                k=p[k].r;  
            else if (p[k].r==-1) //被删除的有孩子节点为空  
                k=p[k].l;  
            else  
                if (p[ p[k].l ].fix < p[ p[k].r ].fix)  //选择孩子节点小的方向旋转  
                {  
                    rot_l(k);  
                    remove(p[k].l,tkey);  
                }  
                else  
                {  
                    rot_r(k);  
                    remove(p[k].r,tkey);  
                }  
        }  
    }  
  
    void print(int k)  //中序遍历  
    {  
        if (p[k].l!=-1)  
            print(p[k].l);  
        cout << p[k].key << " : " << p[k].fix << endl;  
        if (p[k].r!=-1)  
            print(p[k].r);  
    }  
};  
  
treap T;  
  
int main()  
{  
  
    int i;  
    for (i=8;i>=1;i--)  
        T.insert(T.root,i);  
        cout<<"插入节点之后："<<endl;  
    T.print(T.root);  
    for (i=3;i>=1;i--)  
    {  
        cout << "删除key为"<<i<<"的节点："<<endl;  
        T.remove(T.root,i);  
        T.print(T.root);  
    }  
    system("pause");  
    return 0;  
}