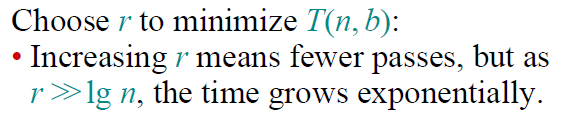MIT算法导论——第五讲.Linear Time Sort
本栏目(Algorithms)下MIT算法导论专题是个人对网易公开课MIT算法导论的学习心得与笔记。所有内容均来自MIT公开课Introduction to Algorithms中Charles E. Leiserson和Erik Demaine老师的讲解。(http://v.163.com/special/opencourse/algorithms.html)
第五节-------线性时间排序 Linear Time Sort
这节课的主要内容是分析基于比较的排序能够达到的最快效率以及介绍几种非比较的线性时间排序算法。
一、排序能够达到的最快效率
目前已经接触了好几种排序的算法,那么有个疑问:排序最快能够达到多快的速度?Θ(n^2),只允许进行相邻数字交换时这个答案正确;Θ(nlgn),这个答案通常是正确的;Θ(n),这个答案也只有在特定情况下也是正确的。所以正确的回答应该是看情况,它取决于你使用的计算模型里,哪些操作是被允许的。在这里主要指的是在排序过程中,哪些操作是被允许的。
目前接触过的算法(插入排序,归并排序,快速排序,堆排序),都是基于比较的排序算法。在比较排序算法模型中,你只能做比较操作来决定元素的相对顺序,也就是我们不能进行整数相乘或者其他奇怪的操作。我们见到过对于基于比较的排序算法来说,最坏情况下的时间复杂度最快的是Θ(nlgn)。那么就有一个疑问,我们能够做的比Θ(nlgn)更快么?决策树能够帮我们回答这个问题。
如上图所示,是对三个元素的序列进行比较排序的决策树分析。其中图中的内部节点标记为i : j的形式表示序列中第i个元素与第j个元素比较;左子树表示如果a[i] <= a[j]的后续比较情况,右子树则表示如果a[i] >= a[j]的后续比较情况;叶子节点即表示从根节点到叶子节点路径所确定的序列的排列顺序。
这就是比较排序的决策树模型。虽然对于一种排序算法画出它的通用的决策树比较困难(决策树的复杂程度是n的指数级),但是我们可以认为任何一种比较排序算法都有其相应的决策树,也就是可以利用决策树来分析算法复杂度情况。算法的运行时间:根节点到叶子节点的路径长度;最坏情况下运行时间:决策树的高度。
下面我们利用决策树分析来证明:任何排序n个元素的决策树的高度是Ω(nlgn)。
由上述证明过程可以知道,决策树的下界问题,也称为基于比较的排序算法的下界问题。具体来说,它说明了归并排序和堆排序算法是渐进最优的。随机化快速排序算法在理想情况下也是渐进最优的。
二、线性时间排序
下面讲的是对比较模型的一个突破,我们要尽量在线性时间内完成排序。我们知道,如果不用并行算法,或者什么超能力,你不可能比线性时间更快完成排序,因为你得去遍历这些数据。无论你做什么,你必须遍历,否则你无法对其正确排序。所以线性时间使我们期望的最好结果。那么我们如何在线性时间内排序?我们需要一些更有效的设想。下面看两种比nlgn快的排序算法。
1. 计数排序
对于计数排序,我们将不用比较的方式,而是对元素做一些其他的操作。我们要做的是假设输入序列是在特定范围内的整数。我们会利用这点来在线性时间内排序。下面是计数排序的伪代码描述。
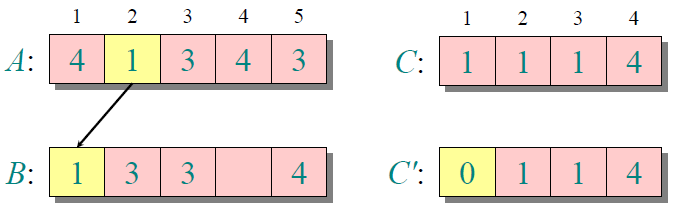
伪代码看起来确实比较费解,下面通过一个例子,分别看看这四个for循环做的事情。第1个for循环简单,初始化将C置0。第2个for循环遍历输入序列A,计算A中等于C对应位置的个数来填充辅助数组C,得到结果:
第3个for循环,做的操作便是计算C中当前位置之前所有数字之和并填充C,得到结果:
第4个for循环,从后往前遍历A中数据,根据C中计算结果,将A中数据放在B中正确的位置。例如A中第一个元素4,则C[4]即为元素4在B中所处的正确位置,即4,也就是目前B中空缺的位置。如下图所示,这样就将A排好序放在了B中。
那好,计算排序算法的算法效率呢?由伪代码可以容易知道,复杂度为Θ(n + k)。如果k = O(n)这极好,我们就得到了线性时间的排序算法。所以看来,我们不仅需要假设这些数是整数,还需要确保这些整数的范围很小。但是从另一方面想,只要k小于nlgn我们就该满意了。所以可以写一个混合算法,如果k比nlgn大我们就用归并排序,如果它比nlgn小就用计数排序。
对于计数排序某个实用的场景:如果你在处理的数字长度为1字节,这就很好。k仅为2^8,这就是256,你需要的辅助数列长度为256,这很快O(256 + n),无论n多大这都是n的线性时间。所以如果你知道数字很小这个算法很好,但是如果数字更大,即使你知道它们仍是整数,但它们是类似于32位的双字,就不是那么简单了。因为这时需要的辅助空间就是2^32,16G。
另外,计数排序是一种稳定排序:对于相等的元素,它保持了他们在输入数列中的顺序。
2. 基数排序
接下来我们要接触一个更有趣的算法,这个算法会利用计数排序作为小数据规模的子程序,结合这个算法那去处理更大规模的数字。
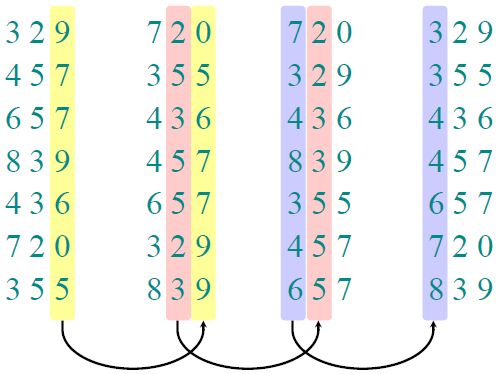
基数排序很可能是最古老实现的算法了,大约出现在1890年,Herman Hollerith应用于卡片分类机器(card-sorting machine)。Herman Hollerith也曾今是MIT的讲师,他发明了最早版本的打孔卡片。基数排序首先对最后一位进行排序,这里就需要用到一种稳定排序算法,然后在对高位进行排序。这个算法让Hollerith赚了很多钱,他在1911年发明了这个制表机,然后在1924年吞并了几个公司组成了一个叫做IBM的新公司,这个可能是你听说过Hollerith的原因。下面就是基数排序的一个例子。
关于这个算法的正确性的证明,我们假设一组数字在他们的低t - 1位已经排好序,那么现在排序第t位。在t位上,对于两个数字不相等的能够正确决定他们的顺序;对于两个数字相等的,基于稳定性原则,可知它们保持原顺序,所以也是正确的。然后根据归纳,我们可以知道它们仍然保持有序的。
接下来分析基数排序的算法复杂度。假设将计数排序作为辅助的稳定排序算法。但是我不想按照每一个数字位来进行依次排序,那样将会失去太多灵活性。因为数可以用任意形式来表示,比如用二进制表示的数,可以把几个比特放在一起当做一位来处理。因此我们假设序列是二进制整数,且为b比特长。
算法把每个整数拆分为b / r位数字,每个数字都是r位长。换句话说,基于2^r禁制来表示这个数。因此,b/r使我们算法需要运行的轮数。而2^r则是每位数字可以取的最大值,某种意义上它是计数排序中的k。那么,总的运行时间怎么算呢?
我们对这个函数关于r求导,求导数为0时的解就可以得到函数的驻点,因此总可以找到最小值。这里将采用某种更直觉的方法,换句话说不那么精确的方法,但是我们还是可以得到正确的结果,当然准确的说是上界。让我们考虑关于r的增长过程,这里有两个包含r的项,r越大那么b/r也就是算法的轮数越少;但是根据后面2^r这一项可知r不可能太大,当r >> lgn时将会指数级的增长。我们想要的是让n而非2^r来决定整个多项式的大小,所以不妨选择r为这种情况下的最大值,即r = lgn。
在实际情况中,基数排序对于大量数据输入运行很快,并且代码易于维护。比如,如果我们有32位的数,我们把它们拆分为比如8位的段,我们仅仅需要做四轮线性时间的运算,只需要256位辅助空间。如果使用nglgn算法,则需要大概11轮,如下图所示。
不幸的是,计数排序在缓存上要求更多,所以在实践中,基数排序并不那么快,除非你的数都很小。快速排序之类的算法会做的更好。
最后提一下,如果对任意整数排序,并且每个数都是一个字长,目前已知的最好的排序算法,期望运行时间是n乘根号下lg(lgn),这是一个随机算法并且非常复杂。有很多非常复杂的算法,但是它们可以给我们某种信息,你可以打破对b的依赖,只要你知道b最多是一个字长。
关于Introduction to Algorithms更多的学习资料将继续更新,敬请关注本博客和新浪微博Sheridan。