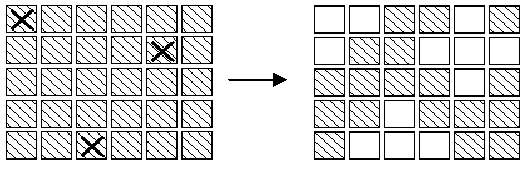
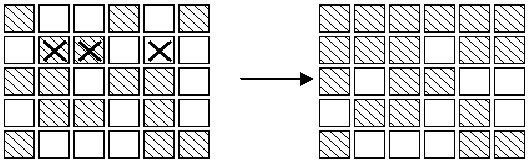
POJ EXTENDED LIGHTS OUT 1222【高斯消元+位运算】
|
Language: Default
EXTENDED LIGHTS OUT
Description
In an extended version of the game Lights Out, is a puzzle with 5 rows of 6 buttons each (the actual puzzle has 5 rows of 5 buttons each). Each button has a light. When a button is pressed, that button and each of its (up to four) neighbors above, below, right and left, has the state of its light reversed. (If on, the light is turned off; if off, the light is turned on.) Buttons in the corners change the state of 3 buttons; buttons on an edge change the state of 4 buttons and other buttons change the state of 5. For example, if the buttons marked X on the left below were to be pressed,the display would change to the image on the right.
The aim of the game is, starting from any initial set of lights on in the display, to press buttons to get the display to a state where all lights are off. When adjacent buttons are pressed, the action of one button can undo the effect of another. For instance, in the display below, pressing buttons marked X in the left display results in the right display.Note that the buttons in row 2 column 3 and row 2 column 5 both change the state of the button in row 2 column 4,so that, in the end, its state is unchanged. 
Note: 1. It does not matter what order the buttons are pressed. 2. If a button is pressed a second time, it exactly cancels the effect of the first press, so no button ever need be pressed more than once. 3. As illustrated in the second diagram, all the lights in the first row may be turned off, by pressing the corresponding buttons in the second row. By repeating this process in each row, all the lights in the first four rows may be turned out. Similarly, by pressing buttons in columns 2, 3 ?, all lights in the first 5 columns may be turned off. Write a program to solve the puzzle. Input
The first line of the input is a positive integer n which is the number of puzzles that follow. Each puzzle will be five lines, each of which has six 0 or 1 separated by one or more spaces. A 0 indicates that the light is off, while a 1 indicates that the light is on initially.
Output
For each puzzle, the output consists of a line with the string: "PUZZLE #m", where m is the index of the puzzle in the input file. Following that line, is a puzzle-like display (in the same format as the input) . In this case, 1's indicate buttons that must be pressed to solve the puzzle, while 0 indicate buttons, which are not pressed. There should be exactly one space between each 0 or 1 in the output puzzle-like display.
Sample Input 2 0 1 1 0 1 0 1 0 0 1 1 1 0 0 1 0 0 1 1 0 0 1 0 1 0 1 1 1 0 0 0 0 1 0 1 0 1 0 1 0 1 1 0 0 1 0 1 1 1 0 1 1 0 0 0 1 0 1 0 0 Sample Output PUZZLE #1 1 0 1 0 0 1 1 1 0 1 0 1 0 0 1 0 1 1 1 0 0 1 0 0 0 1 0 0 0 0 PUZZLE #2 1 0 0 1 1 1 1 1 0 0 0 0 0 0 0 1 0 0 1 1 0 1 0 1 1 0 1 1 0 1 Source
Greater New York 2002
|
高斯消元经典问题
题意：给你一个5*6矩阵的灯，0代表关，1代表开。如果去开一个灯，那么它上下左右的灯的状态就改变。问怎么按这些灯，会关闭所有的灯。
分析：
第一道高斯消元！！！可以将状态考虑成矩阵相乘的形式， 因为是30个灯，所以每个灯的状态，进行所有的状态组合就是一个30*30的矩阵，而每个灯的状态设为一个未知量就有30个未知量，再构造30个方程。就转换为了高斯消元问题。
给定的末状态是b矩阵。初始状态为A矩阵，我们所要求的是就是A的线性组合等于b的情况。如何求这个矩阵？
因为给定的末状态是0矩阵。我们把0矩阵考虑成b矩阵，给定的初状态考虑成A矩阵。
然后我们所要求的就是求解x。
假定A是3*3矩阵：0 1 0
1 1 0
0 1 1
我们需要找出按下每个灯时的作用范围
a(1,1) =
1 1 0
1 0 0
0 0 0
a(2,2)=
0 1 0
1 1 1
0 1 0
我们找出所有灯按下之的影响范围，x代表这个灯是否按下。
我们考虑到A + x(1,1)*a(1,1) + x(1,2)*a(1,2) + x(1,3)*a(1,3) + x(2,1)*a(2,1) + ... + x(3,3)*a(3,3) = 0。
因为是进行的异或运算。我们两边可以同时加上A矩阵。A^A就是0矩阵。所以等式变为：
x(1,1)*a(1,1) + x(1,2)*a(1,2) + x(1,3)*a(1,3) + x(2,1)*a(2,1) + ... + x(3,3)*a(3,3) =A。
然后就是求增广矩阵。a|A。然后就是可以利用高斯消元求出x。
#include <stdio.h>
#include <math.h>
#include <vector>
#include <queue>
#include <string>
#include <string.h>
#include <stdlib.h>
#include <iostream>
#include <algorithm>
using namespace std;
const int MAXN=40;
int equ,var; //equ个方程，var个变元
int x[MAXN]; //解集
int a[MAXN][MAXN];//增广矩阵
int Gauss()
{
int max_r;
int col=0;
//int i,j,k;
for(int k=0;col<=var&&k<equ;k++,col++){
max_r=k;
for(int i=k+1;i<equ;i++) //查找最大变元
if(abs(a[i][col])>abs(a[max_r][col])) max_r=i;
if(max_r!=k) //交换最大变元所在行与当前行
for(int i=col;i<=var;i++)
swap(a[k][i],a[max_r][i]);
if(!a[k][col]){ //当前变元为0，返回上一行
k--;continue;
}
for(int i=k+1;i<equ;i++)
if(a[i][col])//当前变元不为0
for(int j=col;j<=var;j++)
a[i][j]^=a[k][j];
}
for(int i=var-1;i>=0;i--){
x[i]=a[i][var];
for(int j=i+1;j<var;j++)
x[i]^=(a[i][j]&&x[j]);
}
return 0;
}
void init() //初始化A矩阵。为灯的作用范围
{
memset(a,0,sizeof(a));
var=30;
equ=30;
for(int i=0;i<5;i++){
for(int j=0;j<6;j++){
int t=i*6+j;
a[t][t]=1;
if(i>0) a[(i-1)*6+j][t]=1;
if(i<4) a[(i+1)*6+j][t]=1;
if(j>0) a[t][i*6+j-1]=1;
if(j<5) a[t][i*6+j+1]=1;
}
}
}
int main()
{
int T;
scanf("%d",&T);
int xp=1;
while(T--){
init();
for(int i=0;i<30;i++)
scanf("%d",&a[i][30]);
Gauss();
printf("PUZZLE #%d\n",xp++);
for(int i=0;i<30;i++){
if((i+1)%6==0){
printf("%d\n",x[i]);
continue;
}
printf("%d ",x[i]);
}
}
return 0;
}