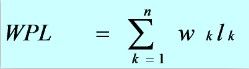哈夫曼树详解

一：什么是哈夫曼树呢？

来看一下百度给的定义吧：给定n个权值作为n个叶子结点，构造一棵二叉树，若带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman tree)。PS：哈夫曼树是在二叉树的基础上定义的。

自己的描述：在树的路径长度的基础上引入了带权路径长度（Weighted Path Length，WPL）。一棵叶子结点带权值（分支节点不带权值）的二叉树叫做扩充二叉树。带权值的结点均为叶子结点，不带权值的均为分支节点（包括根结点），一棵扩充二叉树（带权二叉树）的WPL最小，这么一棵扩充二叉树即为哈夫曼树。下面说明什么是WPL以及如何计算一棵扩充二叉树的WPL：

                                                   

Wk是每一个结点所带的权值，Lk是每一个结点的路径长度。某一个外结点的带权路径长度为：这两个值的乘积，一棵扩充二叉树的带权路径长度则是所有乘积的和了。

二：如何构造一棵哈夫曼树呢？

哈夫曼树构造韩的核心思想就是：要把权值较大的放在离根结点较近的地方，采用自底向上的构造方式。在这里我利用的是最小堆辅助实现的。

1：先来介绍一下我的最小堆吧：

#include<iostream>
#include<vector>
using namespace std;
const int DefaultSize = 10; //默认最小堆数组元素的个数
template<class T>
class MinHeap
{
protected:
	T *heap; //指向一个数组的指针
	int currentSize; //最小堆当前的元素个数
	int maxHeapSize; //最小堆最大能容纳的元素个数
	void SiftDown(int begPos, int endPos); //自上往下调整顺序函数 为对外接口服务 所以置为保护
	void SiftUp(int begPos); //自下往上的调整顺序函数 仍为保护
	void Display();
public:
	MinHeap(int size = DefaultSize); //默认大小的构造函数 构造一个空的最小堆
	MinHeap(T arr[], int elemnum); //接受一个T类型数组地址和元素个数，构造一个最小堆
	~MinHeap(); //析构函数
	bool Insert(const T &elem); //往最小堆里插入一个任意的T类型元素
	bool RemoveMinelem(T &relem); //删除最小堆中的优先级最高的元素即为堆顶元素
	bool IsFull() const; //判最小堆满 定义为常函数
	bool IsEmpty() const; //判最小堆空
	void MakeEmpty(); //置最小堆为空
	template<class T> friend ostream& operator<< (ostream &output, MinHeap<T> &mh); //友元输出一个最小堆
};

template<class T>
void MinHeap<T>::SiftDown(int begPos, int endPos)
{
	int parent_i = begPos;
	int child_j = (2 * parent_i) + 1;
	T temp = heap[parent_i];

	while(child_j <= endPos)
	{
		if((child_j < endPos) && (heap[child_j] > heap[child_j + 1])) //如果当前parent_i结点有分支并且左分支key大于右分支
		{
			child_j++; //则把child_j变量转向右分支 总之child_j记录的是parent_i的左右分支中key较小的那个分支 
		}
		if(temp <= heap[child_j])
		{
			break; //在某次比较中，符合最小堆序关系 则跳出循环
		}
		else
		{
			heap[parent_i] = heap[child_j]; //如果需要进一步的交换，则把当前parent_i，child_j两个变量分别下移一层
			parent_i = child_j;
			child_j = (2 * parent_i) + 1;
		}
	}//end of while

	heap[parent_i] = temp; //跳出循环后的parent_i就指向当前空缺的位置
}

template<class T>
void MinHeap<T>::SiftUp(int begPos)
{
	int child_j = begPos; //开始位置一定是一个孩子节点 具体地说是最后一个节点
	int parent_i = (child_j - 1) / 2; //找到当前孩子节点的双亲
	T temp = heap[child_j];

	while(child_j > 0)
	{
		if(temp < heap[parent_i])
		{
			heap[child_j] = heap[parent_i];
			child_j = parent_i;
			parent_i = (child_j - 1) / 2;
		}
		else
		{
			break;
		}
	}//end of while

	heap[child_j] = temp;
}

template<class T>
void MinHeap<T>::Display()
{
	for(int idx = 0; idx < currentSize; idx++)
	{
		cout<<"#"<<idx + 1<<": "<<heap[idx]<<endl;
	}
}

template<class T>
MinHeap<T>::MinHeap(int size)
{
	maxHeapSize = ((size >= DefaultSize) ? size : DefaultSize);
	heap = new T[maxHeapSize]; //根据最大尺寸开辟元素空间

	if(heap == NULL)
	{
		cerr<<"开辟空间失败!"<<endl;
		exit(1); //强制终止程序
	}

	currentSize = 0; //置当前堆元素大小为0
}

template<class T>
MinHeap<T>::MinHeap(T arr[], int elemnum)
{
	maxHeapSize = ((elemnum >= DefaultSize) ? elemnum : DefaultSize); //确保最小堆的元素空间值最大的
	heap = new T[maxHeapSize];

	if(heap == NULL)
	{
		cerr<<"开辟空间失败!"<<endl;
		exit(1);
	}
	for(int idx = 0; idx < elemnum; idx++)
	{
		heap[idx] = arr[idx]; //从一个数组中把元素依依复制到最小堆空间中
	}

	currentSize = elemnum; //当前最小堆元素个数为源数组元素个数
	int CurrentPos = (currentSize - 2) / 2; //定起始调整位置，即为最小的分支节点，即为最后一个元素的双亲
	
	while(CurrentPos >= 0) //循环调整 直至到最小堆顶
	{
		SiftDown(CurrentPos, currentSize - 1); //调用下调函数
		CurrentPos--; //起始调整位置转到下一个分支节点
	}
}

template<class T>
MinHeap<T>::~MinHeap()
{
	delete []heap; //一定要加上方括号，因为要删除的是一个连续的数组空间，如果不加括号则删除的仅仅是数组的第一个元素，剩下的都将成为"内存黑洞"（被占用的不能被利用的内存空间）
}

template<class T>
bool MinHeap<T>::Insert(const T &elem)
{
	if(currentSize == maxHeapSize)
	{
		cout<<"最小堆满，不能插入!"<<endl;
		return false;
	}

	heap[currentSize] = elem; //放置在堆数组的最后一个
	SiftUp(currentSize); //最后一个叶子节点开始上浮调整
	currentSize++; //当前元素个数加1

	return true;
}

template<class T>
bool MinHeap<T>::RemoveMinelem(T &relem)
{
	if(currentSize == 0)
	{
		cout<<"最小堆为空，无法执行删除操作!"<<endl;
		return false;
	}

	relem = heap[0]; //把最小堆顶元素赋给引用参数relem
	heap[0] = heap[currentSize - 1]; //将最小堆的最后一个元素赋给最小堆顶
	currentSize--; //最小堆元素个数减1
	SiftDown(0,currentSize - 1);

	return true;
}

template<class T>
bool MinHeap<T>::IsEmpty() const
{
	return ((currentSize == 0) ? true : false);
}

template<class T>
bool MinHeap<T>::IsFull() const
{
	return ((currentSize == maxHeapSize - 1) ? true : false);
}

template<class T>
void MinHeap<T>::MakeEmpty()
{
	currentSize = 0; //置最小堆为空
}

template<class T>
ostream& operator<< (ostream &output, MinHeap<T> &mh)
{
	for(int idx = 0; idx < mh.currentSize; idx++)
	{
		output<<"第"<<idx + 1<<"个元素: "<<(mh.heap)[idx]<<endl;
	}

	return output;
}

代码中的注释已经很全了，所以在这里不再赘述，上述代码利用的是模板，所以下面贴的是自定义的类以及主函数中的调用，运行截图等

#pragma once
#include<fstream>
#include<string>
using namespace std;
class City
{
private:
	string m_name;
	int m_key;
public:
	City();
	City(string name, int key);
	~City();
	friend ostream& operator<< (ostream &output, City &C);
	friend ofstream& operator<< (ofstream &foutput, City &C);
	friend istream& operator>> (istream &input, City &C);
	friend ifstream& operator>> (ifstream &finput, City &C);
    void operator= (City &C);
	bool operator<= (City &C);
	bool operator> (City &C);
};

#include<fstream>
#include"City.h"
using namespace std;
City::City()
{

}

City::City(string name, int key)
{
	m_name = name;
	m_key = key;
}

City::~City()
{

}

ostream& operator<< (ostream &output, City &C)
{
	output<<C.m_name<<"  "<<C.m_key ;
	return output;
}

ofstream& operator<< (ofstream &foutput, City &C)
{
	foutput<<C.m_name<<" "<<C.m_key;
	return foutput;
}

istream& operator>> (istream &input, City &C)
{
	input>>C.m_name>>C.m_key;
	return input;
}

ifstream& operator>> (ifstream &finput, City &C)
{
	finput>>C.m_name>>C.m_key;
	return finput;
}

void City::operator= (City &C)
{
	this->m_name = C.m_name;
	this->m_key = C.m_key;
}

bool City::operator<= (City &C)
{
	return ((this->m_key <= C.m_key) ? true : false);
}

bool City::operator> (City &C)
{
	return ((this->m_key > C.m_key) ? true : false);
}

上述自定义类更多的是重载输入输出以及运算符等。

下面是主函数调用：

	City city[8]; //自定义类对象数组
	ifstream in("CITY.txt"); //对象都在文件中

	for(int i = 0; i < 8; i++)
	{
		in>>city[i]; //这里用到文件输入流重载
	}

	MinHeap<City> mheap(city, 8);
	cout<<mheap<<endl;   //上述代码是用来显示最小堆中的各个元素 没有顺序的


	//下面这段代码是每一次取出当前优先级最高的
	City elem;
	for(int i = 0; i < 8; i++)
	{
		mheap.RemoveMinelem(elem);
		cout<<elem<<endl;
	}

运行截图：

好了，先介绍到最小堆的实现，剩下的的在哈夫曼树详解续中介绍。