HDU3511
算法:扫描线
用一条竖直线从左到右扫描所有的圆,处理每个圆“刚接触扫描线”和“刚离开
扫描线”两个事件点。
为了下面描述方便,令某圆A的嵌套层数为f(A), 如果某圆A被某圆B嵌套且A和B
紧邻,那么说A是B的儿子,B是A的父亲。如果圆A,圆B同时是圆C的儿子,那么A,
B互为兄弟,当前考虑的圆为圆C。
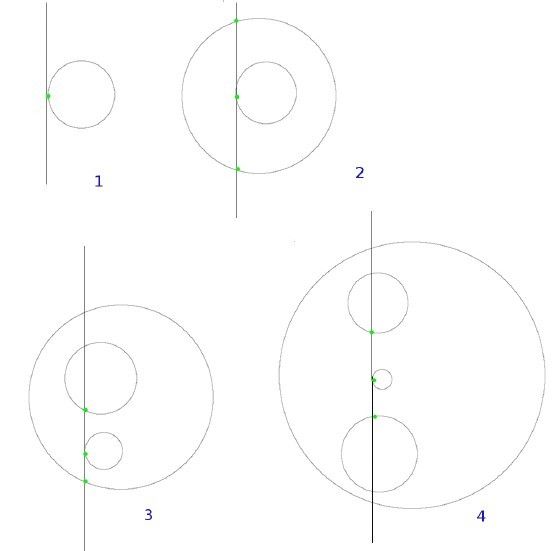
根据“刚接触扫描线”事件点的上下相邻事件点分类有如下情况:
1)没有上方事件点,或者没有下方事件点。这时该圆C的嵌套层数f(C) = 1
2)上方事件点和下方事件点属于同一个圆A,这时圆A必定是圆C的父亲,f(C) =
f(A) + 1
3)上方事件点和下方事件点分别属于两个圆A,B,且f(A) != f(B),这里不妨
设f(A) < f(B),那么A是C的父亲,B是C的兄弟。f(C) = f(A) + 1, f(C) = f(B)
4) 上方事件点和下方事件点分别属于两个圆A,B,且f(A) == f(B),那么A是C
的兄弟,B是C的兄弟,f(C) = f(A) = f(B).
在处理“刚接触扫描线”事件点时插入一对点表示该圆与扫描线的相交情况,
并利用上述分类计算其嵌套层数,在处理“ 刚离开扫描线”事件点是删除对应
的那一对点。可以采用STL 中的set来维护
相关的题目:
http://acm.pku.edu.cn/JudgeOnline/problem?id=2932
http://acmicpc-live-archive.uva.es/nuevoportal/data/problem.php?p=4125
用一条竖直线从左到右扫描所有的圆,处理每个圆“刚接触扫描线”和“刚离开
扫描线”两个事件点。
为了下面描述方便,令某圆A的嵌套层数为f(A), 如果某圆A被某圆B嵌套且A和B
紧邻,那么说A是B的儿子,B是A的父亲。如果圆A,圆B同时是圆C的儿子,那么A,
B互为兄弟,当前考虑的圆为圆C。

根据“刚接触扫描线”事件点的上下相邻事件点分类有如下情况:
1)没有上方事件点,或者没有下方事件点。这时该圆C的嵌套层数f(C) = 1
2)上方事件点和下方事件点属于同一个圆A,这时圆A必定是圆C的父亲,f(C) =
f(A) + 1
3)上方事件点和下方事件点分别属于两个圆A,B,且f(A) != f(B),这里不妨
设f(A) < f(B),那么A是C的父亲,B是C的兄弟。f(C) = f(A) + 1, f(C) = f(B)
4) 上方事件点和下方事件点分别属于两个圆A,B,且f(A) == f(B),那么A是C
的兄弟,B是C的兄弟,f(C) = f(A) = f(B).
在处理“刚接触扫描线”事件点时插入一对点表示该圆与扫描线的相交情况,
并利用上述分类计算其嵌套层数,在处理“ 刚离开扫描线”事件点是删除对应
的那一对点。可以采用STL 中的set来维护
相关的题目:
http://acm.pku.edu.cn/JudgeOnline/problem?id=2932
http://acmicpc-live-archive.uva.es/nuevoportal/data/problem.php?p=4125
#include
<
stdio.h
>
#include < string .h >
#include < math.h >
#include < set >
#include < algorithm >
using namespace std;
const int UP = 0 ;
const int DOWN = 1 ;
const int IN = 0 ;
const int OUT = 1 ;
const int N = 50005 ;
int Time;
struct circle {
int x, y, r;
int w;
void read() {
scanf( " %d %d %d " , & x, & y, & r);
w = 0 ;
}
int getX( int flag) {
if ( flag == IN ) return x - r;
else return x + r;
}
double getY( int flag) {
double ret = sqrt(( double )r * r - ( double )(Time - x) * (Time - x));
if ( flag == UP ) return ( double )y + ret;
else return ( double )y - ret;
}
} cir[N];
struct event {
int x, y, id;
int flag;
void get ( int _x, int _y, int _id, int _flag) {
x = _x;
y = _y;
id = _id;
flag = _flag;
}
bool operator < ( const event ev) const {
return x < ev.x || x == ev.x && y > ev.y;
}
} eve[N * 2 ];
struct node {
int id;
int flag;
node(){}
node( int _id, int _flag) {
id = _id;
flag = _flag;
}
bool operator < ( const node a) const {
double y1 = cir[id].getY(flag);
double y2 = cir[a.id].getY(a.flag);
return y1 > y2 || y1 == y2 && flag < a.flag;
}
};
int n, eveN;
set < node > line;
set < node > ::iterator it, f, e, p;
inline int max( int a, int b) { return a > b ? a : b;}
void moveline() {
line.clear();
for ( int i = 0 ; i < eveN; i ++ ) {
Time = eve[i].x;
if ( eve[i].flag == OUT ) {
line.erase(node(eve[i].id, UP));
line.erase(node(eve[i].id, DOWN));
} else {
it = line.insert(node(eve[i].id, UP)).first;
e = f = it;
e ++ ;
int id = it -> id;
if ( it == line.begin() || e == line.end() ) {
cir[id].w = 1 ;
} else {
f -- ;
if ( f -> id == e -> id ) {
cir[id].w = cir[f -> id].w + 1 ;
} else {
cir[id].w = max( cir[f -> id].w, cir[e -> id].w);
}
}
line.insert(node(eve[i].id, DOWN));
}
}
}
int main() {
while ( scanf( " %d " , & n) != EOF ) {
eveN = 0 ;
for ( int i = 0 ; i < n; i ++ ) {
cir[i].read();
eve[eveN ++ ]. get (cir[i].getX(IN), cir[i].y, i, IN);
eve[eveN ++ ]. get (cir[i].getX(OUT), cir[i].y, i, OUT);
}
sort(eve, eve + eveN);
moveline();
int ans = 0 ;
for ( int i = 0 ; i < n; i ++ ) {
ans = max(ans, cir[i].w);
}
printf( " %d\n " , ans);
}
}
#include < string .h >
#include < math.h >
#include < set >
#include < algorithm >
using namespace std;
const int UP = 0 ;
const int DOWN = 1 ;
const int IN = 0 ;
const int OUT = 1 ;
const int N = 50005 ;
int Time;
struct circle {
int x, y, r;
int w;
void read() {
scanf( " %d %d %d " , & x, & y, & r);
w = 0 ;
}
int getX( int flag) {
if ( flag == IN ) return x - r;
else return x + r;
}
double getY( int flag) {
double ret = sqrt(( double )r * r - ( double )(Time - x) * (Time - x));
if ( flag == UP ) return ( double )y + ret;
else return ( double )y - ret;
}
} cir[N];
struct event {
int x, y, id;
int flag;
void get ( int _x, int _y, int _id, int _flag) {
x = _x;
y = _y;
id = _id;
flag = _flag;
}
bool operator < ( const event ev) const {
return x < ev.x || x == ev.x && y > ev.y;
}
} eve[N * 2 ];
struct node {
int id;
int flag;
node(){}
node( int _id, int _flag) {
id = _id;
flag = _flag;
}
bool operator < ( const node a) const {
double y1 = cir[id].getY(flag);
double y2 = cir[a.id].getY(a.flag);
return y1 > y2 || y1 == y2 && flag < a.flag;
}
};
int n, eveN;
set < node > line;
set < node > ::iterator it, f, e, p;
inline int max( int a, int b) { return a > b ? a : b;}
void moveline() {
line.clear();
for ( int i = 0 ; i < eveN; i ++ ) {
Time = eve[i].x;
if ( eve[i].flag == OUT ) {
line.erase(node(eve[i].id, UP));
line.erase(node(eve[i].id, DOWN));
} else {
it = line.insert(node(eve[i].id, UP)).first;
e = f = it;
e ++ ;
int id = it -> id;
if ( it == line.begin() || e == line.end() ) {
cir[id].w = 1 ;
} else {
f -- ;
if ( f -> id == e -> id ) {
cir[id].w = cir[f -> id].w + 1 ;
} else {
cir[id].w = max( cir[f -> id].w, cir[e -> id].w);
}
}
line.insert(node(eve[i].id, DOWN));
}
}
}
int main() {
while ( scanf( " %d " , & n) != EOF ) {
eveN = 0 ;
for ( int i = 0 ; i < n; i ++ ) {
cir[i].read();
eve[eveN ++ ]. get (cir[i].getX(IN), cir[i].y, i, IN);
eve[eveN ++ ]. get (cir[i].getX(OUT), cir[i].y, i, OUT);
}
sort(eve, eve + eveN);
moveline();
int ans = 0 ;
for ( int i = 0 ; i < n; i ++ ) {
ans = max(ans, cir[i].w);
}
printf( " %d\n " , ans);
}
}