POJ 1085 Triangle War
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 1465 | Accepted: 582 |
Description
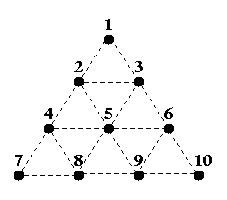
Two players, A and B, take turns filling in any dotted line connecting two dots, with A starting first. Once a line is filled, it cannot be filled again. If the line filled by a player completes one or more triangles, she owns the completed triangles and she is awarded another turn (i.e. the opponent skips a turn). The game ends after all dotted lines are filled in, and the player with the most triangles wins the game. The difference in the number of triangles owned by the two players is not important.
For example, if A fills in the line between 2 and 5 in the partial game on the left below:
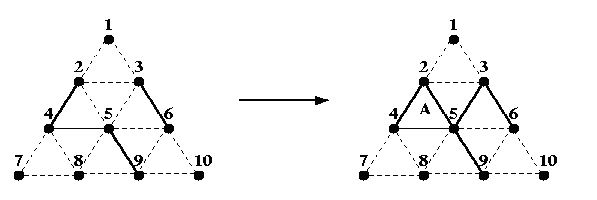
Then, she owns the triangle labelled A and takes another turn to fill in the line between 3 and 5. B can now own 3 triangles (if he wishes) by filling in the line between 2 and 3, then the one between 5 and 6, and finally the one between 6 and 9. B would then make one more move before it is A's turn again.
In this problem, you are given a number of moves that have already been made. From the partial game, you should determine which player will win assuming that each player plays a perfect game from that point on. That is, assume that each player always chooses the play that leads to the best possible outcome for himself/herself.
Input
Output
Sample Input
4 6 2 4 4 5 5 9 3 6 2 5 3 5 7 2 4 4 5 5 9 3 6 2 5 3 5 7 8 6 1 2 2 3 1 3 2 4 2 5 4 5 10 1 2 2 5 3 6 5 8 4 7 6 10 2 4 4 5 4 8 7 8
Sample Output
Game 1: B wins. Game 2: A wins. Game 3: A wins. Game 4: B wins.
Source
dp (博弈)
#include <iostream>
//一共有18条线
#define MAX_LINE 18
//一共有九个三角形
#define MAX_T 9
//状态的最大值是OX3FFFF,所以一共有0X40000个状态
#define MAX_SN 0X40000
using namespace std;
//每条线所在位值的标记
int exp[MAX_LINE + 1] = {0, 0X1, 0x2, 0x4, 0x8, 0x10, 0x20, 0x40, 0x80, 0x100, 0x200, 0x400, 0x800, 0x1000, 0x2000, 0x4000, 0x8000, 0x10000, 0x20000};
//每个三角形的标记,有三角形的三条边的位置决定
int tri[MAX_T + 1][3] =
{
{0, 0, 0},
{exp[1], exp[2], exp[3]},
{exp[4], exp[5], exp[8]},
{exp[3], exp[5], exp[6]},
{exp[6], exp[7], exp[9]},
{exp[10], exp[11], exp[16]},
{exp[8], exp[11], exp[12]},
{exp[12], exp[13], exp[17]},
{exp[9], exp[13], exp[14]},
{exp[14], exp[15], exp[18]}
};
//每条线的标记,有两个顶点的标号决定
int linePID[MAX_LINE + 1][2] =
{
{0, 0}, {1, 2}, {1, 3}, {2, 3}, {2, 4}, {2, 5}, {3, 5},
{3, 6}, {4, 5}, {5, 6}, {4, 7}, {4, 8}, {5, 8},
{5, 9}, {6, 9}, {6, 10}, {7, 8}, {8, 9}, {9, 10}
};
//f是DP的备忘录,用来标记当前状态下,A先走,且AB都按最优走法走条件下,AB取得的三角形个数差值的最大值
int f[MAX_SN + 5], caseN, stepN;
//state状态下,走lineExp这条线新形成的三角形的个数
int takeStep(int state, int lineExp)
{
int i, j, count, triID, num = 0;
//遍历所有的三角形
for(i = 1; i <= MAX_T; i++)
{
//count记录在当前三角形中,已经走过的边的个数
count = 0, triID = -1;
for(j = 0; j < 3; j++)
{
//记录用来表示找到这个边所属的三角形
if(tri[i][j] == lineExp)
triID = j;
else if(state & tri[i][j])
count++;
}
if(triID == -1)
continue;
if(count == 2)
num++;
}
return num;
}
//DP规划解当前状态下,某一方先走,双发都采用最优策略时,双方能达到的最大三角形差值
//这里先走的一方不一定,可以是A,也可以是B
int dpSolve(int curState)
{
//已经计算过了
if(f[curState] != INT_MIN)
return f[curState];
//maxVal:所能达到的最大差值
int maxVal = INT_MIN, i, curVal, extra;
//遍历所有的边
for(i = 1; i <= MAX_LINE; i++)
{
curVal = 0;
//找到一条尚未走的边
if(!(curState & exp[i]))
{
//走这条边可以带来的新的三角形个数
extra = takeStep(curState, exp[i]);
//取得三角形,当前player继续行进
if(extra > 0)
curVal = extra + dpSolve(curState | exp[i]);
else //否则换下一个player
curVal = extra - dpSolve(curState | exp[i]);
//update最大值
if(curVal > maxVal)
maxVal = curVal;
}
}
//记录状态
f[curState] = maxVal;
return maxVal;
}
int main()
{
int cn, i, j, from, to, curVal, curState, totalVal, which;
for(i = 0; i <= MAX_SN; i++)
f[i] = INT_MIN;
//初始状态,当所有线都走掉时,双方都不能走,所以最大差值为0
f[0X3ffff] = 0;
cin>>caseN;
for(cn = 1; cn <= caseN; cn++)
{
totalVal = 0, curState = 0, which = 1; //A先走
cin>>stepN;
for(i = 1; i <= stepN; i++)
{
curVal = 0;
cin>>from>>to;
//遍历所有线找到当前线的标号
for(j = 1; j <= MAX_LINE; j++)
{
if(linePID[j][0] == from && linePID[j][1] == to)
{
//计算走这条线可以带来的差值
curVal = takeStep(curState, exp[j]);
//状态更新
curState |= exp[j];
break;
}
}
//有新三角形被发现,增加差值
if(curVal > 0)
totalVal += which * curVal;
//没有三角形被发现,换另外一个player走
else
which *= -1;
}
//结果输出
char who;
int resP = totalVal + which * dpSolve(curState);
who = (resP > 0) ? 'A' : 'B';
cout<<"Game "<<cn<<":"<<" "<<who<<" wins."<<endl;
}
return 0;
}