LeetCode(134)Gas Station

题目如下：

There are N gas stations along a circular route, where the amount of gas at station i is gas[i].

You have a car with an unlimited gas tank and it costs cost[i] of gas to travel from station i to its next station (i+1). You begin the journey with an empty tank at one of the gas stations.

Return the starting gas station's index if you can travel around the circuit once, otherwise return -1.

Note:
The solution is guaranteed to be unique.

分析如下：

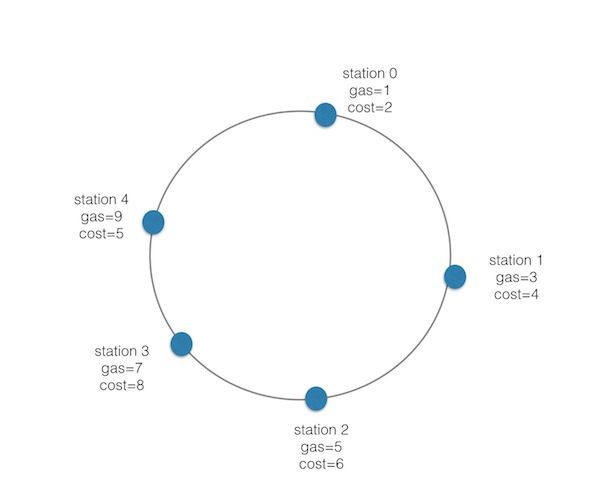
如图，可行的方案就是, 从index = 4的时候开始行动。

对于 N个 station中的每一个点，index 取值范围是[0, N-1]，将这些Index都作为一个可能的起始点，沿着圆圈进行探测。

如果绕行一圈的每个station i 都能保证gas[i] + accumulated >= cost[i], 则可以继续进行到下一个点。其中accumulated 表示目前邮箱里还剩下的没有用完的。

这样的做法是O(N²)，提交发现超时了。

优化的办法是，考虑一下选择起始的station的时候，有限选择gas[i]大且cost[i]小的station。这样首先按照gas[i] - cost[i]进行降序排序。然后根据这个顺序对应的station顺序一次进行探测。

我的代码：

struct gas_index {
    int gas_left;
    int index;
};

bool my_sort_order (struct gas_index a, struct gas_index b)
{
    return (a.gas_left > b.gas_left);
};

class Solution {
public:
    int canCompleteCircuit(vector<int> &gas, vector<int> &cost) {
        vector<struct gas_index> gas_minus_cost;
        for (int i = 0; i < gas.size(); ++i) {
            struct gas_index gi;
            gi.gas_left = gas[i] - cost[i];
            gi.index = i;
            gas_minus_cost.push_back(gi);
        }
        std::sort(gas_minus_cost.begin(), gas_minus_cost.end(), my_sort_order);

        for (int k = 0; k < gas_minus_cost.size(); ++k) {
            int i = gas_minus_cost[k].index;
            if (cost[i] > gas[i]) continue;
                int accumulated_gas = 0, j = 0, current = i;
                for (j = 0; j < gas.size(); ++j) {
                    if (current >= gas.size()) //之前错写为了 if (current > gas.size())
                        current = current % gas.size();
                    if ((accumulated_gas + gas[current]) < cost[current])
                        break;
                    else
                        accumulated_gas = accumulated_gas + gas[current] - cost[current];
                    ++current;
                }
                if (j == gas.size() && ((accumulated_gas + gas[current]) >= cost[current])) 
                // 如果只写if (j == gas.size()是错误的
                    return i;
        }
        return -1;
    }
};