LeetCode(97) Interleaving String

题目如下：

Given s1, s2, s3, find whether s3 is formed by the interleaving of s1 and s2.
For example,
Given:
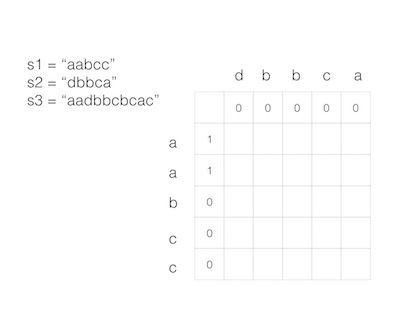
s1 = "aabcc",
s2 = "dbbca",
When s3 = "aadbbcbcac", return true.
When s3 = "aadbbbaccc", return false.
 

分析如下：

        先来理解一下题目大意，从S1和S2中依次，交错地，取一个或者若干个字符，判断是否能够能够形成S3。注意结论成立的隐含条件是， 取字符的过程在S1和S2之间的顺序是交错的，但是在S1内部和S2内部是升序的。

        DFS的思路比较好理解，但是写出来Time limite exceed. 于是想到了用DP，也容易想到，这道题目中length3 = length1  + length2涉及到2维变量，所以应该是个2维动态规划，需要在用2维数组来存储中间计算过程。

        关键是，具体用2维数组表达什么类型的变量，这个不好想，我网上搜了一下，学习了。

        下面的i,j 都是1 base.

dp[i][j] = true，表示s1的前i个字符(s1[0] ~ s[i - 1])和s2(s1[0] ~ s2[j -1])的前j的字符。可以构成s3的前i + j(s3[0] ~ s3[i + j -1])的字符。

        例如， s1 = "aabcc",   s2 = "dbbca"， s3 = "aadbbcbcac",

例如， dp[1][1], 表示s1取前1位a, s2取前1位d，是否能组成s3的前两位aa， 显然false, ad ≠ aa.

        

先来固定i为0，看j。
        dp[0][1], 表示s1取前0位, s2取前1位d，是否能组成s3的前1位， 显然false, d ≠ a.

dp[0][2], 表示s1取前0位, s2取前2位db，是否能组成s3的前2位, 显然false, db≠ aa.

         .......

        dp[0][i], 表示s1取前0位, s2取前i位，是否能组成s3的前i位，

再来固定j为0，看i。

        dp[i][0], 表示s1取前i位, s2取前0位，是否能组成s3的前i位

        那么递推表达式如何写呢？

        当前新加字符(来自s1或者s2)，等于s3里面对应的位( i + j 位)，并且dp[i][j-1] = true或者dp[i-1][j]=true。 这两个条件都具备的情况下，才有dp[i][j] = true.

        按照上面这个规则把2维数组填满。

我的代码:

class Solution {
public:
    bool isInterleave(string s1, string s2, string s3) {
        vector<vector<bool> >  dp(s1.length() + 1, vector<bool> (s2.length() + 1, 0) );
        bool result = false;
        if (s1.length() + s2.length() != s3.length()) return false;
        
        dp[0][0] = 1;

        for (int i = 1; i <= s1.length(); ++i)
            if (dp[i-1][0] == 1 && s1[i - 1] == s3[i - 1])
                dp[i][0] = true;
            else
                break;
                
        for (int i = 1; i <= s2.length(); ++i) 
            if (dp[0][i - 1] == 1 && s2[i - 1] == s3[i - 1]) 
                dp[0][i] = true;
            else
                break;
        
        for (int i = 1; i <= s1.length(); ++i)  {
            for (int j = 1; j <= s2.length(); ++j)  {
                if (dp[i-1][j] == true && s1[i-1] == s3[i+j-1])
                    dp[i][j] = true;
                if (dp[i][j-1] == true && s2[j-1] == s3[i+j-1])
                    dp[i][j] = true;
            }
        } 
        return dp[s1.length()][s2.length() ];
    }
};

扩展小结：

1. edit distance 和 interleaving string这两道题目的共性是都用到了2D的 DP，都在处理String

参考资料：

1 popfish的算法路。 http://blog.csdn.net/u011095253/article/details/9248073