pku2750

pku2750

//参考:
http://hi.baidu.com/fandywang_jlu/blog/item/505b40f4c864bddff3d38574.html
http://blog.csdn.net/ldyhot/archive/2008/10/29/3173535.aspx

  1 /**/ /*
  2线段树+DP 
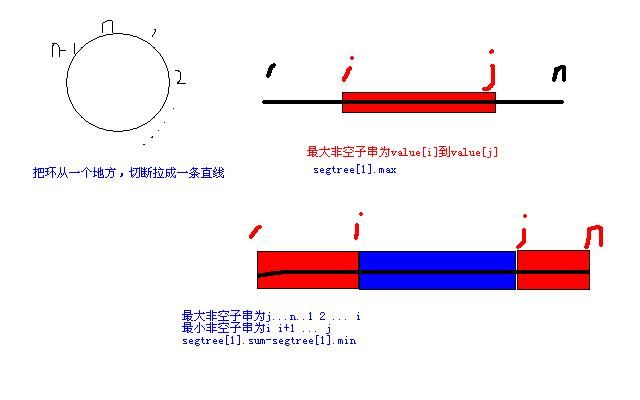
  3        出题者的简单解题报告：把环从一个地方，切断拉成一条直线，
  4        用线段树记录当前区间的非空最大子列和当前区间的非空最小
  5        子列。如果环上的数都是正整数，答案是：环上数的总和－根
  6        结点的非空最小子列；否则，答案是：max{根结点的非空最大
  7        子列, 环上数的总和－根结点的非空最小子列}，每次问答的
  8        复杂度是O(logN)。
  9*/
 10
 11 #include < iostream >
 12 using   namespace  std;
 13 #define  MAXN 100000
 14 #define  MAXM 100000
 15 #define  MAX 262145
 16
 17 struct  Node
 18 {
 19    int left;
 20    int right;
 21    int sum;        //该区间 数的总和 
 22    int max,min;    //该区间 最大子列和 与 最小子列和
 23    int lmax,rmax;    //该区间 从左端点开始的最大子列和 与 到右端点结束的最小子列和
 24    int lmin,rmin;    //该区间 从左端点开始的最小子列和 与 到右端点结束的最小子列和
 25} ;
 26
 27 Node segtree[MAX];
 28 int  value[MAXN + 1 ];
 29 // int vi;
 30
 31 void  update ( int  v)
 32 {
 33    segtree[v].sum=segtree[2*v].sum+segtree[2*v+1].sum;
 34    segtree[v].max=max(max(segtree[2*v].max,segtree[2*v+1].max),segtree[2*v].rmax+segtree[2*v+1].lmax);
 35    segtree[v].min=min(min(segtree[2*v].min,segtree[2*v+1].min),segtree[2*v].rmin+segtree[2*v+1].lmin);
 36    segtree[v].lmax=max(segtree[2*v].lmax, segtree[2*v].sum+segtree[2*v+1].lmax);
 37    segtree[v].rmax=max(segtree[2*v+1].rmax, segtree[2*v+1].sum+segtree[2*v].rmax);
 38    segtree[v].lmin=min(segtree[2*v].lmin,segtree[2*v].sum+segtree[2*v+1].lmin);
 39    segtree[v].rmin=min(segtree[2*v+1].rmin,segtree[2*v+1].sum+segtree[2*v].rmin);
 40}
 41
 42 void  build( int  v, int  l, int  r)
 43 {
 44    segtree[v].left=l;
 45    segtree[v].right=r;
 46
 47    if(l == r )
 48    {
 49        segtree[v].sum =
 50        segtree[v].max = segtree[v].min =
 51        segtree[v].lmax = segtree[v].rmax =
 52        segtree[v].lmin = segtree[v].rmin =value[l];
 53        
 54    }else
 55    {
 56        
 57        int mid=(segtree[v].left+segtree[v].right)>>1;
 58        build(2*v,l,mid);
 59        build(2*v+1,mid+1,r);
 60        update(v);
 61    }
 62    
 63}
 64
 65 void  insert( int  v, int  index)
 66 {
 67    if( segtree[v].left == segtree[v].right && segtree[v].left == index)
 68    {
 69        segtree[v].sum =
 70        segtree[v].max = segtree[v].min =
 71        segtree[v].lmax = segtree[v].rmax =
 72        segtree[v].lmin = segtree[v].rmin =value[index];
 73    }else
 74    {
 75        int mid=(segtree[v].left+segtree[v].right)>>1;
 76        if(index <= mid) insert(2*v,index);
 77        else insert(2*v+1,index);
 78        //if(index <= segtree[2*v].right) insert(2*v,index);
 79        //else if(index >= segtree[2*v+1].left) insert(2*v+1,index);
 80        update(v);
 81    }
 82}
 83
 84 int  main()
 85 {
 86    int n,k,i,index;
 87    scanf("%d",&n);
 88    for(i=1;i<=n;i++)
 89        scanf("%d",&value[i]);
 90
 91    build(1,1,n);
 92
 93    scanf("%d",&k);
 94    while(k--)
 95    {
 96        scanf("%d",&index);
 97        scanf("%d",&value[index]);
 98        insert(1,index);
 99        if(segtree[1].sum==segtree[1].max)
100            printf("%d\n",segtree[1].sum-segtree[1].min);
101        else printf("%d\n",max(segtree[1].max,segtree[1].sum-segtree[1].min));
102    }
103    return 0;
104}
105