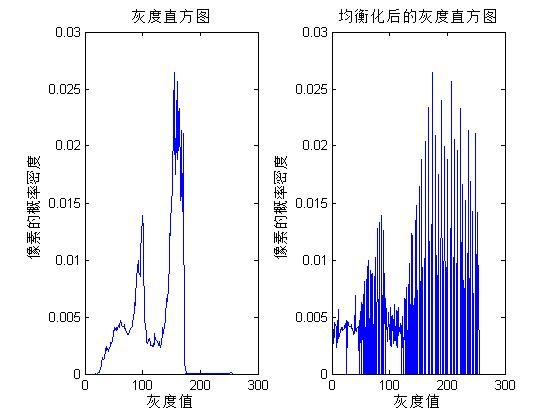
matlab-直方图小结

图像的像素灰度变化是随机的，直方图的图形高低不齐，直方图均衡化就是用一定的算法使直方图大致平和。
均衡化处理后的图像只能是近似的均匀分布，均衡化图像的动态范围扩大了，但其本质是扩大了量化间隔，而量化级别反而减少了
因此，原来灰度不同的像素经处理后可能变的相同，形成了一片的相同灰度的区域，各区域之间有明显的边界，从而出现了伪轮廓
如果原始图像对比度就很高，如果在均衡化则灰度调和，对比度降低。
在泛白缓和的图像中，均衡化会合并一些像素灰度，从而增大对比度。
均衡化后的图片如果在对其均衡化，则图像不会有任何变化


基本算法：
就是把直方图的每个灰度级进行归一化处理，
求每种灰度的累积分布，得到一个映射的灰度映射表，
然后根据相应的灰度值来进行修正原图中的每个像素。


经典的直方图均衡化算法可能存在以下一些不足：
1.输出图像的实际灰度变化范围很难达到图像格式所允许的最大灰度变化范围
2.输出图像的灰度分布直方图虽然接近均匀分布，但其值与理想值1/n仍有可能存在较大的差异，并非是最佳值
3.输出图像的灰度级有可能被过多的合并，由于灰度的吞噬也易造成图像信息的丢失


概率密度函数(PDF)
为了计算方便，我们需要将直方图归一化，即把灰度范围有0~255变为0~1.
归一化后的直方图其实就是一个概率密度函数(PDF-probability density function),均衡化就是令概率密度为1。
我们利用Pr(r)来表示原始图像的PDF，用Ps(s)表示均衡化之后的PDF，r、s分别表示均衡化前后的灰度值，r、s在[0,1]
根据概率论的知识可知：

  ;  是T(r)的逆变函数

两边对r进行积分，即可得出PDF的均衡化公式

累积分布函数(CDF-cumulative distribution function)
对于图像而言，我们需要使用离散形式的公式(Discrete Formulation)
某个灰度级像素出现的概率为Pr(rk)=nk/N
Pr(rk)是远原图像第K个灰度级像素出现的概率，rk是第k个灰度级，即当前色阶k，在[0,1]。
nk是rk像素数量，N是像素总数(图像大小)
图像的灰度直方图均衡化公式:

clear all
close all
clc

I=imread('1.jpg');   
I_gray=rgb2gray(I);    
graydis=zeros(1,256);          
new_graydis=zeros(1,256);
[row col]=size(I_gray);
new_img=zeros(row,col);

for x=1:row
     for y=1:col
         graydis(1,I_gray(x,y))=graydis(1,I_gray(x,y))+1;
     end
end

%计算原始直方图
graydispro=graydis./sum(graydis);
subplot(1,2,1);
plot(graydispro);
title('灰度直方图');
xlabel('灰度值');ylabel('像素的概率密度');

%计算原始累计直方图-CDF
for i=2:256
    graydispro(1,i)=graydispro(1,i)+graydispro(1,i-1);
end

%计算和原始灰度对应的新的灰度T[]，建立映射关系
for i=1:256
    T(1,i)=floor(254*graydispro(1,i)+0.5);
end

%统计新直方图各灰度级像素个数
for i=1:256
    new_graydis(1,T(1,i)+1)=new_graydis(1,T(1,i)+1)+graydis(1,i);
end

%计算新的灰度直方图
new_graydispro=new_graydis./sum(new_graydis);
subplot(1,2,2);
plot(new_graydispro);
title('均衡化后的灰度直方图');
xlabel('灰度值');ylabel('像素的概率密度');

%计算直方图均衡后的图像
for x=1:row
    for y=1:col
      new_img(x,y)=T(1,I_gray(x,y));
    end
end
figure,imshow(I_gray);
title('原图');
figure,imshow(new_img,[]);
title('直方图均衡化后的图');