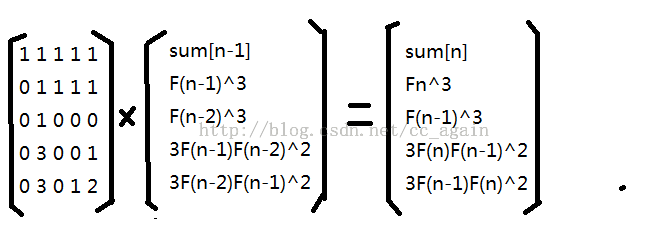第三届华中区全国程序设计大赛暨武大校赛网赛
卷首语:
好长时间没敲题,太水了。。。。思维慢死了。。。。
Problem 1537 - A - Stones I
题目链接:
http://acm.whu.edu.cn/land/problem/detail?problem_id=1537
题目意思:
有n堆石头,第i堆有ai和bi属性,每次拿一堆(假设第i堆)后,所有的石头的a值都减去bi.求最后拿到的a的和的最大值。
解题思路:
枚举。
题目本质意思就是求拿了m堆后 sigma(a)-m*sigma(b)的最大值。枚举m,按ai-m*bi排序,求出前面的m个和,再比较求出最大值。
代码:
#include<iostream>
#include<cstdlib>
#include<cstdio>
#include<algorithm>
#include<cstring>
#define ll long long
using namespace std;
#define Maxn 1100
struct Node
{
ll a,b,v;
}t1[Maxn];
ll n,ans;
bool cmp(struct Node a,struct Node b)
{
return a.v>b.v;
}
ll MM(ll a,ll b)
{
return a>b?a:b;
}
int main()
{
while(scanf("%lld",&n)&&n)
{
for(int i=1;i<=n;i++)
{
scanf("%lld%lld",&t1[i].a,&t1[i].b);
t1[i].v=t1[i].a-t1[i].b;
}
sort(t1+1,t1+n+1,cmp);
ans=t1[1].v;
for(int i=2;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
t1[j].v=t1[j].a-i*t1[j].b;
}
sort(t1+1,t1+n+1,cmp);
ll temp=0;
for(int j=1;j<=i;j++)
temp+=t1[j].v;
ans=MM(ans,temp);
// printf("i:%d %lld\n",i,ans);
}
printf("%lld\n",ans);
}
return 0;
}
题目链接:
http://acm.whu.edu.cn/land/problem/detail?problem_id=1538
题目意思:
有n堆石头,每拿一堆(假设是第i堆),没有被拿的石头堆的a都要减去bi,求能够拿的a的和的最大值。
解题思路:
动态规划+贪心
挖掘题目意思,可知当要选剩余堆的个数j确定下来后,当前堆对后面的影响是a[i]-b[i]*j.后面有多少个堆就要减多少次。
分析知当堆确定后,a值不会对结果产生影响,只有b值会产生影响,显然b小的放到前面结果更优。所以先按b值从小到大排序。
dp[i][j]:表示第i堆后还要选j堆能达到的最大值。
转移方程:
dp[i][j]=max(dp[i-1][j],dp[i-1][j+1]+a[i]-b[i]*j) ; //要么选要么不选
代码:
//#include<CSpreadSheet.h>
#include<iostream>
#include<cmath>
#include<cstdio>
#include<sstream>
#include<cstdlib>
#include<string>
#include<string.h>
#include<cstring>
#include<algorithm>
#include<vector>
#include<map>
#include<set>
#include<stack>
#include<list>
#include<queue>
#include<ctime>
#include<bitset>
#define eps 1e-6
#define INF 0x3f3f3f3f
#define PI acos(-1.0)
#define ll __int64
#define LL long long
#define lson l,m,(rt<<1)
#define rson m+1,r,(rt<<1)|1
#define M 1000000007
//#pragma comment(linker, "/STACK:1024000000,1024000000")
using namespace std;
#define Maxn 1100
struct Inf
{
int a,b;
}save[Maxn];
LL dp[Maxn][Maxn];
int n;
LL Max(LL a,LL b)
{
return a>b?a:b;
}
bool cmp(struct Inf a,struct Inf b)
{
return a.b<b.b;
}
int main()
{
//freopen("in.txt","r",stdin);
//freopen("out.txt","w",stdout);
while(scanf("%d",&n)&&n)
{
for(int i=1;i<=n;i++)
scanf("%lld%lld",&save[i].a,&save[i].b);
memset(dp,-INF,sizeof(dp)); //无效状态
//printf("%d\n",dp[1][1]);
sort(save+1,save+n+1,cmp); //顺序 肯定对b从小到大比较优
for(int i=0;i<=n;i++)
dp[0][i]=0;
for(int i=1;i<=n;i++)
{
for(int j=0;j<=n;j++)
dp[i][j]=Max(dp[i-1][j],dp[i-1][j+1]+save[i].a-save[i].b*j);
}
printf("%lld\n",dp[n][0]);
}
return 0;
}
Problem 1540 - D - Fibonacci
http://acm.whu.edu.cn/land/problem/detail?problem_id=1540
题目意思:
求斐波拉契数列的前n项的立方和(n<=10^9) 第一项和第二项是1、1
解题思路:
矩阵快速幂
构造矩阵
F(n)^3=(F(n-1)+F(n-2))^3=F(n-1)^3+F(n-2)^3+3*F(n-1)^2*F(n-2)+3*F(n-1)*F(n-2)^2
代码:
//#include<CSpreadSheet.h>
#include<iostream>
#include<cmath>
#include<cstdio>
#include<sstream>
#include<cstdlib>
#include<string>
#include<string.h>
#include<cstring>
#include<algorithm>
#include<vector>
#include<map>
#include<set>
#include<stack>
#include<list>
#include<queue>
#include<ctime>
#include<bitset>
#define eps 1e-6
#define INF 0x3f3f3f3f
#define PI acos(-1.0)
#define ll __int64
#define LL long long
#define lson l,m,(rt<<1)
#define rson m+1,r,(rt<<1)|1
#define M 1000000007
//#pragma comment(linker, "/STACK:1024000000,1024000000")
using namespace std;
#define Maxn 8
LL n;
struct Mar
{
int row,col;
LL s[Maxn][Maxn];
void init(int a,int b)
{
row=a;
col=b;
memset(s,0,sizeof(s));
}
};
Mar operator * (const Mar &a,const Mar &b)
{
Mar c;
c.init(a.row,b.col);
for(int k=1;k<=a.col;k++)
for(int i=1;i<=a.row;i++)
{
if(!a.s[i][k])
continue;
for(int j=1;j<=b.col;j++)
{
if(!b.s[k][j])
continue;
c.s[i][j]=(c.s[i][j]+(a.s[i][k]*b.s[k][j])%M+M)%M;
}
}
return c;
}
Mar ans,ba;
void init()
{
ans.init(5,1);
ans.s[1][1]=2,ans.s[2][1]=1,ans.s[3][1]=1,ans.s[4][1]=3,ans.s[5][1]=3;
ba.init(5,5);
for(int i=1;i<=5;i++)
ba.s[1][i]=1;
for(int i=2;i<=5;i++)
ba.s[2][i]=1;
ba.s[3][2]=1;
ba.s[4][2]=3;
ba.s[4][5]=1;
ba.s[5][2]=3;
ba.s[5][4]=1;
ba.s[5][5]=2;
}
int main()
{
//freopen("in.txt","r",stdin);
//freopen("out.txt","w",stdout);
while(scanf("%lld",&n)&&n)
{
if(n==1)
{
printf("1\n");
continue;
}
if(n==2)
{
printf("2\n");
continue;
}
n-=2;
init();
while(n)
{
if(n&1)
ans=ba*ans;
n>>=1;
ba=ba*ba;
}
printf("%lld\n",ans.s[1][1]);
}
return 0;
}