卷积神经网络(Convolutional Neural Networks)
最近看了卷积神经网络,在此记录一下自己的心得体会。
1. 卷积神经网络的结构
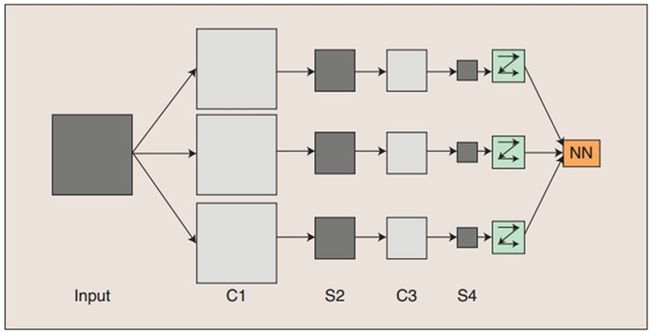
卷积神经网络由多层神经网络构成,每层包含多个二维平面,每个平面包含多个独立的神经元。
在以上途中,输入图像与三个可训练的滤波器和可加偏置进行卷积,卷积后的结果在C1层产生三个特征映射图(Feature Maps),然后每个特征映射图中的四个相邻像素再进行求和,加权值,加偏置,通过一个Sigmoid函数得到三个S2层的特征映射图。这些映射图再经过滤波得到C3层,然后经过与C1->S2一样的过程产生S4。最终,这些像素值被光栅化,并连接成一个向量输入到传统的神经网络,得到输出。
一般地,C层为特征提取层,每个神经元的输入与前一层的局部感受野相连,并提取该局部的特征,一旦该局部特征被提取后,它与其他特征间的位置关系也随之确定下来;S层是特征映射层(计算层),网络的每个计算层由多个特征映射组成,每个特征映射为一个平面,平面上所有神经元的权值相等。特征映射采用sigmoid函数作为卷积网络的激活函数,使得特征映射具有位移不变性。
此外,由于一个映射面上的神经元共享权值,因而减少了网络自由参数的个数,降低了网络参数选择的复杂度。卷积神经网络中的每一个特征提取层(C-层)都紧跟着一个用来求局部平均与二次提取的计算层(S-层),这种特有的两次特征提取结构使网络在识别时对输入样本有较高的畸变容忍能力。
2. 局部感受野与权值共享
2.1局部感受野
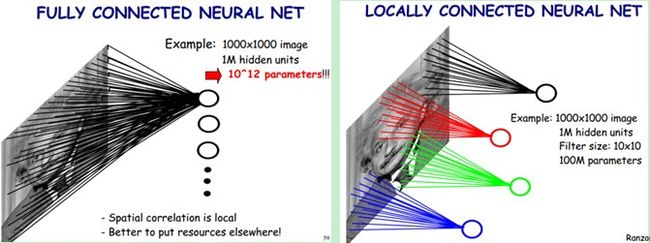
上图左:全连接网络。如果我们有1000x1000像素的图像,有1百万个隐层神经元,每个隐层神经元都连接图像的每一个像素点,就有1000x1000x1000000=10^12个连接,也就是10^12个权值参数。
上图右:局部连接网络,每一个节点与上层节点同位置附件10x10的窗口相连接,则1百万个隐层神经元就只有100w乘以100,即10^8个参数。其权值连接个数比原来减少了四个数量级。
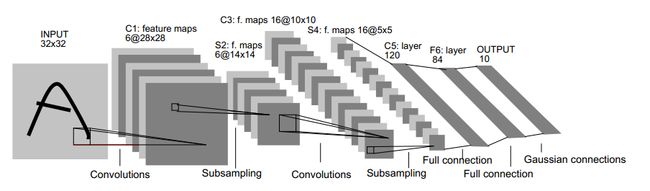
2.2 权值共享1) 输入图像是32x32的大小,局部滑动窗的大小是5x5的,由于不考虑对图像的边界进行拓展,则滑动窗将有28x28个不同的位置,也就是C1层的大小是28x28。这里设定有6个不同的C1层,每一个C1层内的权值是相同的。
2) S2层是一个下采样层。简单的说,由4个点下采样为1个点,也就是4个数的加权平均。但在LeNet-5系统,下采样层比较复杂,因为这4个加权系数也需要学习得到,这显然增加了模型的复杂度。在斯坦福关于深度学习的教程中,这个过程叫做Pool。
3) 根据对前面C1层同样的理解,我们很容易得到C3层的大小为10x10. 只不过,C3层的变成了16个10x10网络。如果S2层只有1个平面,那么由S2层得到C3就和由输入层得到C1层是完全一样的。但是,S2层由多层,那么,我们只需要按照一定的顺利组合这些层就可以了。具体的组合规则,在LeNet-5 系统中给出了下面的表格:
简单的说,例如对于C3层第0张特征图,其每一个节点与S2层的第0张特征图,第1张特征图,第2张特征图,总共3个5x5个节点相连接。后面依次类推,C3层每一张特征映射图的权值是相同的。
4)S4 层是在C3层基础上下采样,前面已述。在后面的层由于每一层节点个数比较少,都是全连接层,这个比较简单,不再赘述。
简化的LeNet-5系统把下采样层和卷积层结合起来,避免了下采样层过多的参数学习过程,同样保留了对图像位移,扭曲的鲁棒性。其网络结构图如下所示: