搜索——Ny 90 整数划分
1) 题目
整数划分
时间限制:3000 ms | 内存限制:65535 KB
难度:3
描述
将正整数n表示成一系列正整数之和:n=n1+n2+…+nk,
其中n1≥n2≥…≥nk≥1,k≥1。
正整数n的这种表示称为正整数n的划分。求正整数n的不
同划分个数。
例如正整数6有如下11种不同的划分:
6;
5+1;
4+2,4+1+1;
3+3,3+2+1,3+1+1+1;
2+2+2,2+2+1+1,2+1+1+1+1;
1+1+1+1+1+1。
输入
第一行是测试数据的数目M(1<=M<=10)。以下每行均包含一个整数n(1<=n<=10)。
输出
输出每组测试数据有多少种分法。
样例输入
1
6
样例输出
11
2) 题意
不再赘述。
3) 数据范围
测试数据数和n的值最大为10,数据量很小,手算都很容易。
4) 算法
搜索法
为了避免搜索到重复的划分方法,规定:
划分序列a1+a2+…+an,ai>=ai+1, 1<=i<n。
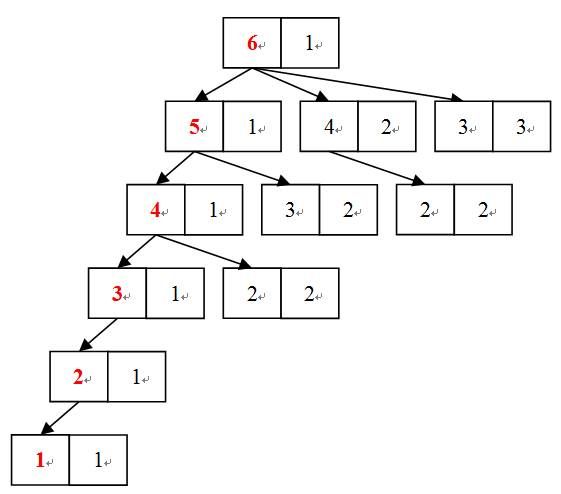
如下图是划分整数6的一棵搜索树。两方格内的数字是划分出的两个数。如6可以划分为5+1,4+2,3+3。
图中以红色数字为根节点一棵树,即为该红色数字的划分搜索树。
5) 代码
#include <iostream>
#include <cstdio>
#include <ctime>
using namespace std;
int count;
//num为要划分的数,minn为允许划分出的最小数
void Backtrack(int num, int minn)
{
//printf("%d %d\n", num, minn);
count++;
if (num > 1)
{
int left, right;
for (left = num-minn, right = minn; left >= right; left--, right++)
{
Backtrack(left, right);
}
}
}
int main(void)
{
int ncases;
scanf("%d", &ncases);
while (ncases-- != 0)
{
int num;
scanf("%d", &num);
count = 0;
//clock_t start, finish;
//start = clock();
Backtrack(num, 1);
//finish = clock();
//printf("%lf\n", (double)(finish - start) / CLOCKS_PER_SEC);
printf("%d\n", count);
}
return 0;
}
/*
#include<iostream>
using namespace std;
int q(int n,int m)
{
if((n<1)||(m<1) )return 0;
if(n==1||m==1) return 1;
if(n<m) return q(n,n);
if(n==m)return q(n,m-1)+1;
return q(n,m-1)+q(n-m,m);
}
int main()
{
int a;
cin>>a;
while(a--)
{
int n;
cin>>n;
cout<<q(n,n)<<endl;
}
return 0;
}
*/
6) 测试数据
10
1
2
3
4
5
6
7
8
9
7) 提交结果
第一次,没有按输入格式来,粗心。