《Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification》阅读笔记与实现

　　本期要讲的是来自MSRA的何恺明的论文《Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification》，这篇论文是首次公开宣布图像的识别率超越人类水平的文章，其象征性意义确实巨大，论文出炉时也有很多报道，但我们今天不谈这些，只关注其技术细节。

一、Sigmoid，ReLU与Leaky ReLU

1、ReLU的引入

　　这几年的神经网络，尤其是卷积神经网络取得如此巨大的成功，受到很多人的不解：我看现在这些网络结构跟90年代的LeNet没有什么不同，为什么现在“突然”就引来了一轮革命？纵然有计算机性能上的巨大提升，GPU的应用使得我们可以在短时间内得到一个庞大的模型，难道在算法上就没有本质变化吗？
　　答案是有的，有一些虽然不起眼，但其实是质变的技术引领了这次变革，其中首推的就是ReLU（Rectified Linear Units）。传统的神经元模型使用的激活函数是sigmoid，它是从神经科学上边仿生过来的，用它来模拟神经元从受到刺激，接收到的电信号超过一定的阈值就产生兴奋这个特性确实是很恰当的，在神经网络的第二波浪潮中也确实解决了很多问题，然而它有一个严重的问题就是其容易产生饱和效应，也称梯度弥散效应，就是在sigmoid函数的两侧是平的（下图所示，抱歉我把上期的图拿来了），即梯度非常小，在一个深层的神经网络模型中，有很多神经元的都是在这个函数的两边，这就使得梯度累加起来的和在反向传播的过程中会越来越小，在上一期我们也做过实验，梯度确实会越来越小，导致前边几层根本无法得到有效地训练，之前大牛们也想过一些办法，例如只使用梯度的符号进行迭代，但这是个治标不治本的办法。

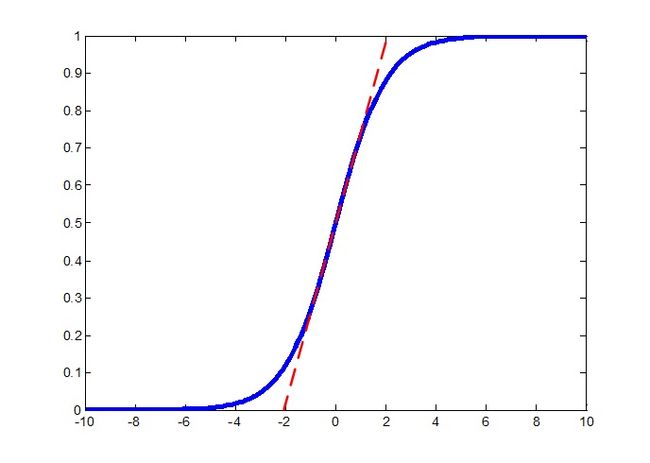
　　ICCV2009上Lecun组发表了一篇文章《What is the Best Multi-Stage Architecture for Object Recognition?》，窃以为应当列为深度学习奠基性文章之一，这篇文章使用的激活函数 y=abs(x) 已经非常接近ReLU了，而且在介绍其激活函数的时候有这么一句：Several rectifying non-linearities weretried, including the positive part, and produced similar results. 这实际上就是现在使用最多的ReLU了，只是他们在Cifar这种小数据集上做的实验发现二者性能相当。实际上，深层神经网络的数学本质是“使用多层的非线性函数逼近任意非线性函数”，我们需要的实际上只是一个非线性函数而已，为何要使用sigmoid、tanh这类还需要计算指数、三角函数的复杂函数呢？因此， abs(x) 、 max(x,0) 这类函数进入了研究人员的视线，对于计算机来说，计算它们只需要动动符号位，而且它们的梯度很简单，就是1或者-1或者0，不论传播多少层，其梯度和都会维持在一个相对稳定的数量级上，这样就解决了纠结了10余年的梯度弥散问题。

2、ReLU的几何意义

　　说了这么半天ReLU对神经网络产生的深远影响，实际上ReLU神经元的数学表达式非常简单：

y=max(0,Wx+b)

　　画成图就是（左图，右图为Leaky ReLU）：
　　
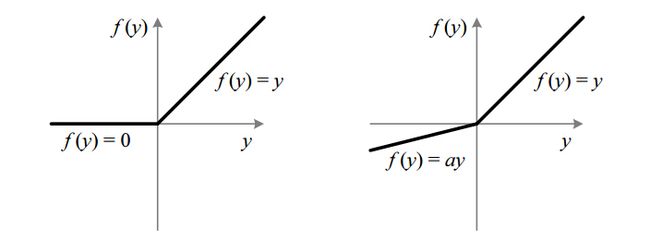
　　这样的一个激活函数对数据会产生什么样的影响呢？注意到， Wx+b=0 是一个超平面，在这个超平面的两侧， x 受到了不同的对待： Wx+b<0 的部分，函数值直接被“挤压”至0，而 Wx+b>0 的部分，函数值保持不变，画成图就是

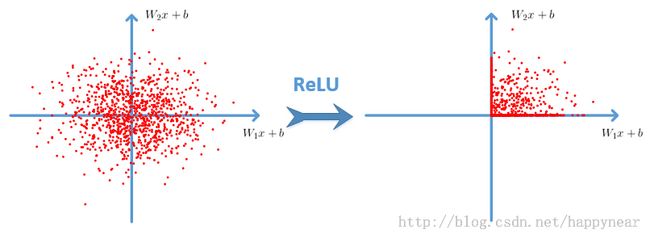
　　下方的数据点被推向横轴，左侧的数据点被推向了纵轴，形成了两条数据非常密集的直线（高维上就是超平面）。注意上图中，两个 Wx+b 被画成了正交的，通常在一个训练好的神经网络模型中，它们并不是正交的。非正交的情况、高维的情况需要读者自行想象。
　　上图说明，只有一个象限（抱歉我不知道高维空间里面这个词叫什么，还是就叫象限吧）的信息被保留了，而其他象限的信息被不同程度地压缩了，而且压缩幅度非常大，使其完全无法恢复。这其实是非常不合理的，也许这里仍旧有一些可以加以区分的信息被压缩没了，当然，这些信息在其他卷积核中也许会有所体现，但这样断绝一切可能性的做法并不可取，因此便有了Leaky ReLU的想法。

3、Leaky ReLU

　　Leaky ReLU的数学表达式如下：

y=max(0,Wx+b)+αmin(0,Wx+b)

　　在负半轴加了一个斜率 α ，不再是直接压缩至0了，而是将负数部分压缩 α 倍，表现在图形上就是：

　　这样，既起到了修正数据分布的作用，又不一棍打死，在后面几层需要负轴这边信息的时候不至于完全无法恢复。

二、Parametric ReLU

1、计算过程

　　在这篇论文出现之前，已经有人对Leaky ReLU进行了探索，CAFFE上也早已有了相关的实现，但一般都是指定 α 的值，例如0.1或者0.2，之前Kaggle上的CIFAR-10竞赛，冠军就用了类似的黑科技（链接）。然而可以观察到，损失函数对 α 的导数我们是可以求得的，可不可以将它作为一个参数进行训练呢？这篇论文指出，不仅可以训练，而且效果更好。
　　公式非常简单，反向传播至未激活前的神经元的公式就不写了，很容易就能得到。对 α 的导数如下：

∂yi∂α={0,if yi>0yi,if yi≤0

　　在matlab上实现的代码如下：
　　前向传播：

nn.a_hat{i} = nn.a{i};
nn.a{i} = max(nn.a_hat{i}, 0) + nn.ra(i - 1) * min(nn.a_hat{i}, 0);

　　反向传播:

d_act = (nn.a_hat{i} > 0) + nn.ra(i - 1) * (nn.a_hat{i} < 0);
tt = d{i}(nn.a_hat{i} < 0) .* nn.a_hat{i}(nn.a_hat{i} < 0);
nn.da(i - 1) = sum(tt) / size(nn.a{i}, 1);

　　注意到，如果 α 为负数，即类似 abs(x) 的情况，激活后的值就是非负的了，无法从激活值判断未激活状态下的符号，因此我们需要保留下原始的符号信息。

2、初始化方法

　　实际上，我觉得本文最大的贡献不在于提出了leaky relu的斜率可以求导，而是神经网络初始化的方法，众所周知，深度神经网络的参数很难调整，很多新手在使用nn或者cnn模型的时候，甚至会发现损失函数值一直都不下降，于是去改学习率，改初始化权重的尺度，费时费力。实际上，只要函数能下降，我们总会得到一个还算满意的结果，再去调整网络结构之类的参数也更加有信心。我就在2个月前训练一个汉字识别模型的时候，还算遇到了损失函数无法下降的问题，最后莫名其妙的就解决了，搞得我小心翼翼的，生怕动了哪里又无法训练了。
　　看到这篇论文后，我立刻在matlab中进行了实现，说实话，那酸爽…现在可以随便设置多么深的网络进行训练了，完全不用每次都为初始化参数问题折腾半天，记得当时的挫败感和对deep learning的怀疑，现在再也不复存在了。
(1) 理论推导
　　本文提出的初始化方法基于方差的计算，对于一个卷积层或者全连接层，其表达式为：

yl=Wlxl+bl.

　　若 Wl 、 bl 采样自0均值高斯分布，用 nl 表示第 l 层 xl 的维数，在卷积层，有 nl=k2c ，k为卷积核的边长，c为channel数，注意到 yl 是 Wl 中元素与 xl 中对应元素的乘积的和，则上式各变量的方差关系可以表示为：

Var[yl]=nlVar[Wlxl]=nlVar[Wl]E[x2l].

　　这里的 xl 项前并不是其方差，而是 E[x2l] ，因为 xl 通常并不具备0均值，例如ReLU激活函数得到的结果， xl 均为正值。注意到由于 Wl 是0均值的，所以无论 xl 均值为多少，均有
　　

E[yl]=E[Wlxl]=0.

　　通过ReLU激活函数： xl=max(0,yl−1) ，仅正半轴有值，可以得到：

E[x2l]=12Var[yl].

　　于是，得到方差表达式：

Var[yl]=12nlVar[Wl]Var[yl].

　　若我们希望每一层的 y 都有同样的方差，例如方差全部为1，就得到：

12nlVar[Wl]=1.

　　即， Wl 从 N(0,2nl) 中采样，即可使每层的 Var[y] 均为1.
　　对于Leaky Relu来说， 因为负方向也有取值，所以

E[x2l]=12(1+α2)Var[yl].

　　通过类似的推导，可知 Wl 从 N(0,2(1+α2)nl) 中采样，即可使每层的 Var[y] 均为1.
(2) Matlab实现
　　matlab中，我们使用randn函数从标准正态分布 N(0,1) 中采样，每层的 Wl 初始化为：

nn.W{i - 1} = randn(nn.size(i), nn.size(i - 1)+1) * sqrt(2 / (nn.size(i - 1)) / (1 + nn.ra(i-1)^2));

　　完整代码在我的Github（https://github.com/happynear/DeepLearnToolbox）上有，读者可以下载下来试用一下。

3、实验

　　文章中用一个深度达30层的网络将文中的初始化方法与之前比较通用的Xavier方法做了对比，结果如下：
　　
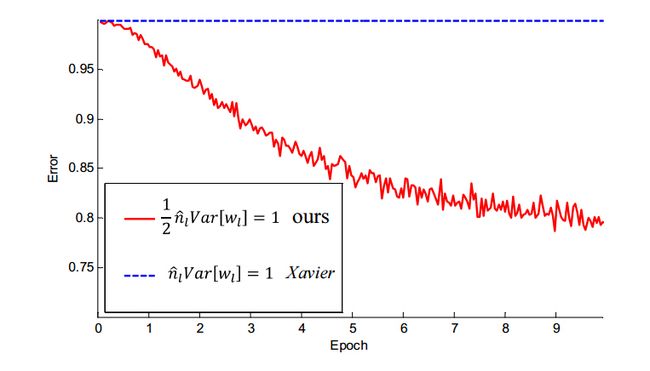
　　图中的表述有点错误，实际上Xavier是从均匀分布中采样的。可以看到，Xavier初始化碰到了经常困扰我们的问题：损失函数不下降，而文中提出的方法即使在30层网络中，依然能够良好地优化。但是，文中说30层网络的效果却不如VGG的19层和他们使用的22层网络，看来imagenet所需的网络容量我们已经能够达到了，那么现实世界需要多少呢？
　　原文说使用了Parametric ReLU后，最终效果比不用提高了1.03%，这个结果我并没有条件进行验证，期待各大实验室的复现结果。

4、关于稀疏

　　我们都知道，由于之前的神经网络使用ReLU激活函数，最终我们提取到的特征（分类器之前一层的输出值）是有50%的稀疏度的，即有50%的神经元输出为0。稀疏的方法在之前10年终也频频出现在人们的视野中，有大量的理论的、工程的论文来描述它。而加了稀疏约束的AutoEncoder、包括稀疏字典训练算法在RBG图像上得到的权重，像极了在imagenet上监督式训练得到的第一层甚至第二层权重的值，这给人一种错觉：一个“好”的特征表达必须是稀疏的？
　　这篇论文给出了相反的答案，稀疏并不是必要条件，稠密的特征能够得到更好的结果。之前以标榜稀疏的论文（如DeepID2+），利用稀疏性，将特征二值化，也能得到优良的分类性能，实际上使用PReLU、采用正/负的二值化，应该也能得到类似的结果。
　　我对稀疏方法研究得并不深入，但我一直对稀疏类的方法持怀疑态度，在我的实验结果中，稀疏表达、稀疏分类器并不能取得很好的效果。稀疏向量、稀疏矩阵究竟是我们一厢情愿的结果，为了稀疏而稀疏，还是稀疏真的对分类、对回归、对重建有效？我觉得以后应当更加辨证地看待这个问题，仔细检验稀疏先验是否与数据的经验分布相符，再决定是否增加一项 λ∥x∥1 。
　　欢迎与我的观点持不同意见的读者与我进行讨论。