我写的一个 C++ 复数类
我的C++ 的基础一直都不太扎实,最近有点空闲时间,找了本 C++ Primer 仔细的读了读。看完运算符重载那一章时,就想到写个复数类来练一练手。
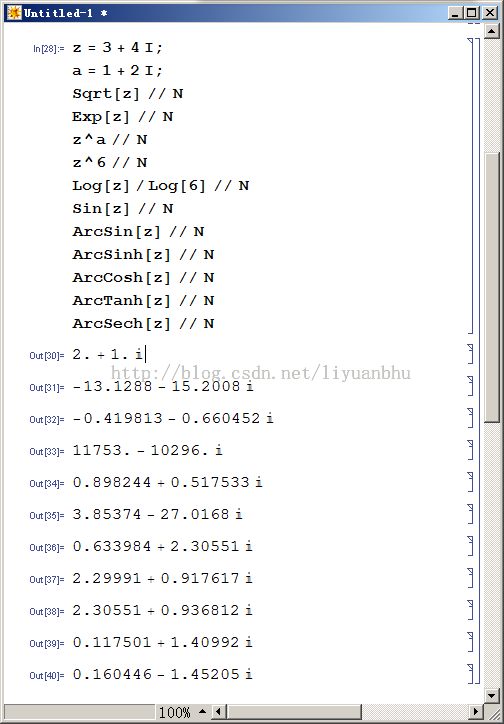
实际上 C++ 中是有复数类的,而且还是个模版类,比我这个类用起来更灵活。不过我的类也有自己的特点,就是支持相当多的数学函数,那些函数相应的代码是从 GSL 中借来的,所以计算结果还算是可靠的,大多数的函数的计算结果 都用 Mathematica 验算过了,看起来还算是挺靠谱的。
下面先贴出头文件。
#ifndef COMPLEX_H
#define COMPLEX_H
#include <iostream>
class Complex
{
public:
Complex(const Complex &z);
Complex(double x = 0.0, double y = 0.0);
~Complex();
double real() const {return dat[0];}
double image() const {return dat[1];}
double abs() const {return hypot(dat[0], dat[1]);}
void set(double x, double y) {dat[0] = x; dat[1] = y;}
inline double arg() const;
inline double abs2() const;
inline double logabs () const;
Complex conjugate() const;
Complex inverse() const;
Complex operator +(const Complex &other) const;
Complex operator +(const double &other) const;
Complex operator -(const Complex &other) const;
Complex operator -(const double &other) const;
Complex operator *(const Complex &other) const;
Complex operator *(const double &other) const;
Complex operator /(const Complex &other) const;
Complex operator /(const double &other) const;
void operator +=(const Complex &other);
void operator +=(const double &other);
void operator -=(const Complex &other);
void operator -=(const double &other);
void operator *=(const Complex &other);
void operator *=(const double &other);
void operator /=(const Complex &other);
void operator /=(const double &other);
Complex& operator =(const Complex &other);
Complex& operator =(const double &other);
private:
double dat[2];
friend std::ostream& operator << (std::ostream&, const Complex & z);
friend Complex operator -(const Complex &other);
};
Complex sqrt(const Complex& a);
Complex exp(const Complex& a);
Complex pow(const Complex& a, const Complex& b);
Complex pow(const Complex& a, double b);
Complex log(const Complex& a);
Complex log10 (const Complex &a);
Complex log(const Complex &a, const Complex &b);
// 三角函数
Complex sin (const Complex& a);
Complex cos (const Complex& a);
Complex tan (const Complex& a);
Complex cot (const Complex& a);
Complex sec (const Complex& a);
Complex csc (const Complex& a);
// 反三角函数
Complex arcsin_real (double a);
Complex arccos_real(double a);
Complex arcsec_real (double a);
Complex arctan_real (double a);
Complex arccsc_real(double a);
Complex arcsin (const Complex& a);
Complex arccos (const Complex& a);
Complex arctan (const Complex& a);
Complex arcsec (const Complex& a);
Complex arccsc (const Complex& a);
Complex arccot (const Complex& a);
/**********************************************************************
* Complex Hyperbolic Functions
**********************************************************************/
Complex sinh (const Complex& a);
Complex cosh (const Complex& a);
Complex tanh (const Complex& a);
Complex sech (const Complex& a);
Complex csch (const Complex& a);
Complex coth (const Complex& a);
/**********************************************************************
* Inverse Complex Hyperbolic Functions
**********************************************************************/
Complex arccoth (const Complex& a);
Complex arccsch (const Complex& a);
Complex arcsech (const Complex& a);
Complex arctanh_real (double a);
Complex arctanh (const Complex& a);
Complex arccosh_real (double a);
Complex arccosh (const Complex& a);
Complex arcsinh (const Complex& a);
Complex polar(double r, double theta);
double fabs(const Complex &z);
#endif // COMPLEX_H
复数的实部和虚部存在了一个数组中,而不是放到两个double型变量中,这样做也是遵循了 GSL 的代码,据GSL 的作者解释,这样可以最大限度的保证 实部和虚部是连续放置的。代码还算简单,这里就对几个重点做些解释。
Complex operator +(const Complex &other) const;
operator + 必须要声明为 const。否则下面的代码无法通过编译。
const Complex a(1, 2); const Complex b(2, 3); Complex c = a + b;
另外 operator - 需要定义两个函数,有一个是
Complex operator -(const Complex &other);这个函数是为了类似如下代码使用的
c = -a + b;
实际上这个函数不用声明为 友元函数,因为它不需要访问越权访问Complex 的私有变量。之所以这么写只是想用一下 friend 关键字。不过我个人认为外部函数还是不应该越权访问类的私有变量的,因此 friend 用的越少越好。所以后面实现的各种数学函数都没有声明为友元函数。
下面是Complex 的基本实现。
#include "complex.h"
#include <cmath>
Complex::Complex(double x, double y)
{
dat[0] = x;
dat[1] = y;
}
Complex::Complex(const Complex &z)
{
dat[0] = z.dat[0];
dat[1] = z.dat[1];
}
Complex::~Complex()
{
}
double Complex::arg() const
{
double x = dat[0];
double y = dat[1];
if (x == 0.0 && y == 0.0)
{
return 0;
}
return std::atan2 (y, x);
}
double Complex::abs2() const
{
double x = dat[0];
double y = dat[1];
return (x * x + y * y);
}
double Complex::logabs () const
{
double xabs = fabs (dat[0]);
double yabs = fabs (dat[1]);
double max, u;
if (xabs >= yabs)
{
max = xabs;
u = yabs / xabs;
}
else
{
max = yabs;
u = xabs / yabs;
}
/* Handle underflow when u is close to 0 */
return log (max) + 0.5 * log1p (u * u);
}
Complex Complex::conjugate() const
{
Complex z(dat[0], -dat[1]);
return z;
}
Complex Complex::inverse() const
{
double s = 1.0 / fabs (*this);
double x = this->real();
double y = this->image();
Complex z(x * s * s, - y * s * s);
return z;
}
void Complex::operator +=(const Complex &other)
{
dat[0] += other.dat[0];
dat[1] += other.dat[1];
}
void Complex::operator +=(const double &other)
{
dat[0] += other;
}
void Complex::operator -=(const Complex &other)
{
dat[0] -= other.dat[0];
dat[1] -= other.dat[1];
}
void Complex::operator -=(const double &other)
{
dat[0] -= other;
}
void Complex::operator *=(const Complex &other)
{
double x, y;
x = (dat[0] * other.dat[0] - dat[1] * other.dat[1]);
y = (dat[1] * other.dat[0] + dat[0] * other.dat[1]);
dat[0] = x;
dat[1] = y;
}
void Complex::operator *=(const double &other)
{
dat[0] = dat[0] * other;
dat[1] = dat[1] * other;
}
void Complex::operator /=(const Complex &other)
{
double x, y;
double a = other.dat[0] * other.dat[0] + other.dat[1] * other.dat[1];
x = ((dat[0] * other.dat[0]) + (dat[1] * other.dat[1])) / a;
y = ((dat[1] * other.dat[0]) - (dat[0] * other.dat[1])) / a;
dat[0] = x;
dat[1] = y;
}
void Complex::operator /=(const double &other)
{
dat[0] = dat[0]/other;
dat[1] = dat[1]/other;
}
Complex Complex::operator+(const Complex &other) const
{
Complex temp(*this);
temp += other;
return temp;
}
Complex Complex::operator +(const double &other) const
{
Complex temp(*this);
temp += other;
return temp;
}
Complex Complex::operator -(const Complex &other) const
{
Complex temp(*this);
temp -= other;
return temp;
}
Complex Complex::operator -(const double &other) const
{
Complex temp(*this);
temp -= other;
return temp;
}
Complex operator -(const Complex &other)
{
Complex temp(-other.real(), -other.image());
return temp;
}
Complex Complex::operator *(const Complex &other) const
{
Complex temp(*this);
temp *= other;
return temp;
}
Complex Complex::operator *(const double &other) const
{
Complex temp(*this);
temp *= other;
return temp;
}
Complex Complex::operator /(const Complex &other) const
{
Complex temp(*this);
temp /= other;
return temp;
}
Complex Complex::operator /(const double &other) const
{
Complex temp(*this);
temp /= other;
return temp;
}
Complex& Complex::operator =(const Complex &other)
{
this->dat[0] = other.dat[0];
this->dat[1] = other.dat[1];
return *this;
}
Complex& Complex::operator =(const double &other)
{
this->dat[0] = other;
this->dat[1] = 0;
return *this;
}
std::ostream& operator << (std::ostream& out, const Complex & z)
{
out << "real = " << z.dat[0] << std::endl;
out << "image = " << z.dat[1] << std::endl;
return out;
}
一些基本数学函数的实现代码如下:
Complex polar(double r, double theta)
{
Complex z(r * cos(theta), r * sin(theta));
return z;
}
double fabs(const Complex &z)
{
return hypot(z.real(), z.image());
}
Complex sqrt(const Complex& a)
{
Complex z;
if (a.real() == 0.0 && a.image() == 0.0)
{
z = Complex(0, 0);
}
else
{
double x = fabs (a.real());
double y = fabs (a.image());
double w;
if (x >= y)
{
double t = y / x;
w = sqrt (x) * sqrt (0.5 * (1.0 + sqrt (1.0 + t * t)));
}
else
{
double t = x / y;
w = sqrt (y) * sqrt (0.5 * (t + sqrt (1.0 + t * t)));
}
if (a.real() >= 0.0)
{
double ai = a.image();
z.set (w, ai / (2.0 * w));
}
else
{
double ai = a.image();
double vi = (ai >= 0) ? w : -w;
z.set( ai / (2.0 * vi), vi);
}
}
return z;
}
Complex exp(const Complex& a)
{
double rho = exp (a.real());
double theta = a.image();
Complex z(rho * cos (theta), rho * sin (theta));
return z;
}
Complex pow(const Complex& a, const Complex& b)
{ /* z=a^b */
Complex z;
if (a.real() == 0 && a.image() == 0.0)
{
if (b.real() == 0 && b.image() == 0.0)
{
z.set(1.0, 0.0);
}
else
{
z.set( 0.0, 0.0);
}
}
else if (b.real() == 1.0 && b.image() == 0.0)
{
return a;
}
else if (b.real() == -1.0 && b.image() == 0.0)
{
return a.inverse();
}
else
{
double logr = a.logabs();
double theta = a.arg();
double br = b.real(), bi = b.image();
double rho = exp (logr * br - bi * theta);
double beta = theta * br + bi * logr;
z.set( rho * cos (beta), rho * sin (beta));
}
return z;
}
Complex pow(const Complex &a, double b)
{ /* z=a^b */
Complex z;
if (a.real() == 0 && a.image() == 0)
{
if (b == 0)
{
z.set( 1, 0);
}
else
{
z.set( 0, 0);
}
}
else
{
double logr = a.logabs();
double theta = a.arg();
double rho = exp (logr * b);
double beta = theta * b;
z.set( rho * cos (beta), rho * sin (beta));
}
return z;
}
Complex log (const Complex &a)
{ /* z=log(a) */
double logr = a.logabs();
double theta = a.arg();
Complex z(logr, theta);
return z;
}
Complex log10 (const Complex &a)
{ /* z = log10(a) */
return log (a) / log (10.0);
}
Complex log(const Complex &a, const Complex &b)
{
return log (a) / log (b);
}
Complex sin (const Complex& a)
{ /* z = sin(a) */
double R = a.real(), I = a.image();
Complex z;
if (I == 0.0)
{
/* avoid returing negative zero (-0.0) for the imaginary part */
z.set( sin (R), 0.0);
}
else
{
z.set( sin (R) * cosh (I), cos (R) * sinh (I));
}
return z;
}
Complex cos (const Complex& a)
{
double R = a.real(), I = a.image();
Complex z;
if (I == 0.0)
{
/* avoid returing negative zero (-0.0) for the imaginary part */
z.set(cos (R), 0.0);
}
else
{
z.set( cos (R) * cosh (I), sin (R) * sinh (-I));
}
return z;
}
Complex tan (const Complex& a)
{
double R = a.real(), I = a.image();
Complex z;
if (fabs (I) < 1)
{
double D = pow (cos (R), 2.0) + pow (sinh (I), 2.0);
z.set( 0.5 * sin (2 * R) / D, 0.5 * sinh (2 * I) / D);
}
else
{
double u = exp (-I);
double C = 2 * u / (1 - pow (u, 2.0));
double D = 1 + pow (cos (R), 2.0) * pow (C, 2.0);
double S = pow (C, 2.0);
double T = 1.0 / tanh (I);
z.set( 0.5 * sin (2 * R) * S / D, T / D);
}
return z;
}
Complex cot (const Complex& a)
{ /* z = cot(a) */
Complex z = tan (a);
return z.inverse();
}
Complex sec (const Complex& a)
{
Complex z = cos (a);
return z.inverse();
}
Complex csc (const Complex& a)
{
Complex z = sin (a);
return z.inverse();
}
Complex arcsin_real(double a)
{ /* z = arcsin(a) */
Complex z;
if (fabs (a) <= 1.0)
{
z.set( asin (a), 0.0);
}
else
{
if (a < 0.0)
{
z.set( -M_PI_2, acosh (-a));
}
else
{
z.set( M_PI_2, -acosh (a));
}
}
return z;
}
Complex arcsin (const Complex& a)
{ /* z = arcsin(a) */
double R = a.real(), I = a.image();
Complex z;
if (I == 0)
{
z = arcsin(R);
}
else
{
double x = fabs (R), y = fabs (I);
double r = hypot (x + 1, y), s = hypot (x - 1, y);
double A = 0.5 * (r + s);
double B = x / A;
double y2 = y * y;
double real, imag;
const double A_crossover = 1.5, B_crossover = 0.6417;
if (B <= B_crossover)
{
real = asin (B);
}
else
{
if (x <= 1)
{
double D = 0.5 * (A + x) * (y2 / (r + x + 1) + (s + (1 - x)));
real = atan (x / sqrt (D));
}
else
{
double Apx = A + x;
double D = 0.5 * (Apx / (r + x + 1) + Apx / (s + (x - 1)));
real = atan (x / (y * sqrt (D)));
}
}
if (A <= A_crossover)
{
double Am1;
if (x < 1)
{
Am1 = 0.5 * (y2 / (r + (x + 1)) + y2 / (s + (1 - x)));
}
else
{
Am1 = 0.5 * (y2 / (r + (x + 1)) + (s + (x - 1)));
}
imag = log1p (Am1 + sqrt (Am1 * (A + 1)));
}
else
{
imag = log (A + sqrt (A * A - 1));
}
z.set( (R >= 0) ? real : -real, (I >= 0) ? imag : -imag);
}
return z;
}
Complex arccos (const Complex& a)
{ /* z = arccos(a) */
double R = a.real(), I = a.image();
Complex z;
if (I == 0)
{
z = arccos(R);
}
else
{
double x = fabs (R), y = fabs (I);
double r = hypot (x + 1, y), s = hypot (x - 1, y);
double A = 0.5 * (r + s);
double B = x / A;
double y2 = y * y;
double real, imag;
const double A_crossover = 1.5, B_crossover = 0.6417;
if (B <= B_crossover)
{
real = acos (B);
}
else
{
if (x <= 1)
{
double D = 0.5 * (A + x) * (y2 / (r + x + 1) + (s + (1 - x)));
real = atan (sqrt (D) / x);
}
else
{
double Apx = A + x;
double D = 0.5 * (Apx / (r + x + 1) + Apx / (s + (x - 1)));
real = atan ((y * sqrt (D)) / x);
}
}
if (A <= A_crossover)
{
double Am1;
if (x < 1)
{
Am1 = 0.5 * (y2 / (r + (x + 1)) + y2 / (s + (1 - x)));
}
else
{
Am1 = 0.5 * (y2 / (r + (x + 1)) + (s + (x - 1)));
}
imag = log1p (Am1 + sqrt (Am1 * (A + 1)));
}
else
{
imag = log (A + sqrt (A * A - 1));
}
z.set( (R >= 0) ? real : M_PI - real, (I >= 0) ? -imag : imag);
}
return z;
}
Complex arccos_real(double a)
{ /* z = arccos(a) */
Complex z;
if (fabs (a) <= 1.0)
{
z.set( acos (a), 0);
}
else
{
if (a < 0.0)
{
z.set( M_PI, -acosh (-a));
}
else
{
z.set( 0, acosh (a));
}
}
return z;
}
Complex arctan (const Complex& a)
{ /* z = arctan(a) */
double R = a.real(), I = a.image();
Complex z;
if (I == 0)
{
z.set( atan (R), 0);
}
else
{
/* FIXME: This is a naive implementation which does not fully
take into account cancellation errors, overflow, underflow
etc. It would benefit from the Hull et al treatment. */
double r = hypot (R, I);
double imag;
double u = 2 * I / (1 + r * r);
/* FIXME: the following cross-over should be optimized but 0.1
seems to work ok */
if (fabs (u) < 0.1)
{
imag = 0.25 * (log1p (u) - log1p (-u));
}
else
{
double A = hypot (R, I + 1);
double B = hypot (R, I - 1);
imag = 0.5 * log (A / B);
}
if (R == 0)
{
if (I > 1)
{
z.set( M_PI_2, imag);
}
else if (I < -1)
{
z.set( -M_PI_2, imag);
}
else
{
z.set( 0, imag);
};
}
else
{
z.set( 0.5 * atan2 (2 * R, ((1 + r) * (1 - r))), imag);
}
}
return z;
}
Complex arcsec (const Complex& a)
{ /* z = arcsec(a) */
Complex z = a.inverse();
return arccos(z);
}
Complex arcsec_real (double a)
{ /* z = arcsec(a) */
Complex z;
if (a <= -1.0 || a >= 1.0)
{
z.set( acos (1 / a), 0.0);
}
else
{
if (a >= 0.0)
{
z.set( 0, acosh (1 / a));
}
else
{
z.set( M_PI, -acosh (-1 / a));
}
}
return z;
}
Complex arccsc (const Complex& a)
{ /* z = arccsc(a) */
Complex z = a.inverse();
return arcsin (z);
}
Complex arccsc_real(double a)
{ /* z = arccsc(a) */
Complex z;
if (a <= -1.0 || a >= 1.0)
{
z.set( asin (1 / a), 0.0);
}
else
{
if (a >= 0.0)
{
z.set( M_PI_2, -acosh (1 / a));
}
else
{
z.set(-M_PI_2, acosh (-1 / a));
}
}
return z;
}
Complex arccot (const Complex& a)
{ /* z = arccot(a) */
Complex z;
if (a.real() == 0.0 && a.image() == 0.0)
{
z.set( M_PI_2, 0);
}
else
{
z = a.inverse();
z = arctan (z);
}
return z;
}
双曲函数的实现代码:
Complex sinh (const Complex& a)
{ /* z = sinh(a) */
double R = a.real(), I = a.image();
Complex z;
z.set( sinh (R) * cos (I), cosh (R) * sin (I));
return z;
}
Complex cosh (const Complex& a)
{ /* z = cosh(a) */
double R = a.real(), I = a.image();
Complex z;
z.set( cosh (R) * cos (I), sinh (R) * sin (I));
return z;
}
Complex tanh (const Complex& a)
{ /* z = tanh(a) */
double R = a.real(), I = a.image();
Complex z;
if (fabs(R) < 1.0)
{
double D = pow (cos (I), 2.0) + pow (sinh (R), 2.0);
z.set( sinh (R) * cosh (R) / D, 0.5 * sin (2 * I) / D);
}
else
{
double D = pow (cos (I), 2.0) + pow (sinh (R), 2.0);
double F = 1 + pow (cos (I) / sinh (R), 2.0);
z.set( 1.0 / (tanh (R) * F), 0.5 * sin (2 * I) / D);
}
return z;
}
Complex sech (const Complex& a)
{ /* z = sech(a) */
Complex z = cosh (a);
return z.inverse();
}
Complex csch (const Complex& a)
{ /* z = csch(a) */
Complex z = sinh (a);
return z.inverse();
}
Complex coth (const Complex& a)
{ /* z = coth(a) */
Complex z = tanh (a);
return z.inverse();
}
/**********************************************************************
* Inverse Complex Hyperbolic Functions
**********************************************************************/
Complex arcsinh (const Complex& a)
{ /* z = arcsinh(a) */
Complex z = a * Complex(0, 1.0);
z = arcsin (z);
z *= Complex(0, -1);
return z;
}
Complex arccosh (const Complex& a)
{ /* z = arccosh(a) */
Complex z = arccos (a);
if(z.image() > 0)
{
z *= Complex(0, -1);
}
else
{
z *= Complex(0, 1);
}
return z;
}
Complex arccosh (double a)
{ /* z = arccosh(a) */
Complex z;
if (a >= 1)
{
z.set( acosh (a), 0);
}
else
{
if (a >= -1.0)
{
z.set( 0, acos (a));
}
else
{
z.set( acosh (-a), M_PI);
}
}
return z;
}
Complex arctanh (const Complex& a)
{ /* z = arctanh(a) */
if (a.image() == 0.0)
{
return arctanh (a.real());
}
else
{
Complex z = a * Complex(0, 1.0);
z = arctan (z);
z = z * Complex(0, -1.0);
return z;
}
}
Complex arctanh_real (double a)
{ /* z = arctanh(a) */
Complex z;
if (a > -1.0 && a < 1.0)
{
z.set( atanh (a), 0);
}
else
{
z.set( atanh (1 / a), (a < 0) ? M_PI_2 : -M_PI_2);
}
return z;
}
Complex arcsech (const Complex& a)
{ /* z = arcsech(a); */
Complex t = a.inverse();
return arccosh (t);
}
Complex arccsch (const Complex& a)
{ /* z = arccsch(a) */
Complex t = a.inverse();
return arcsinh (t);
}
Complex arccoth (const Complex& a)
{ /* z = arccoth(a) */
Complex t = a.inverse();
return arctanh (t);
}
上面的代码中用到了些不在标准库中的数学函数,比如:
double acosh (const double x); double atanh (const double x); double asinh (const double x); double log1p (const double x);
这几个函数的实现可以参考下面的代码:
#define GSL_SQRT_DBL_EPSILON 1.4901161193847656e-08
#define GSL_DBL_EPSILON 2.2204460492503131e-16
#ifndef M_LN2
#define M_LN2 0.69314718055994530941723212146 /* ln(2) */
#endif
inline double fdiv(double a, double b)
{
return a / b;
}
inline double nan (void)
{
return fdiv (0.0, 0.0);
}
inline double posinf (void)
{
return fdiv (+1.0, 0.0);
}
inline double neginf (void)
{
return fdiv (-1.0, 0.0);
}
double log1p (const double x)
{
volatile double y, z;
y = 1 + x;
z = y - 1;
return log(y) - (z - x) / y ; /* cancels errors with IEEE arithmetic */
}
double acosh (const double x)
{
if (x > 1.0 / GSL_SQRT_DBL_EPSILON)
{
return log (x) + M_LN2;
}
else if (x > 2)
{
return log (2 * x - 1 / (sqrt (x * x - 1) + x));
}
else if (x > 1)
{
double t = x - 1;
return log1p (t + sqrt (2 * t + t * t));
}
else if (x == 1)
{
return 0;
}
else
{
return nan();
}
}
double asinh (const double x)
{
double a = fabs (x);
double s = (x < 0) ? -1 : 1;
if (a > 1 / GSL_SQRT_DBL_EPSILON)
{
return s * (log (a) + M_LN2);
}
else if (a > 2)
{
return s * log (2 * a + 1 / (a + sqrt (a * a + 1)));
}
else if (a > GSL_SQRT_DBL_EPSILON)
{
double a2 = a * a;
return s * log1p (a + a2 / (1 + sqrt (1 + a2)));
}
else
{
return x;
}
}
double atanh (const double x)
{
double a = fabs (x);
double s = (x < 0) ? -1 : 1;
if (a > 1)
{
return nan();
}
else if (a == 1)
{
return (x < 0) ? neginf() : posinf();
}
else if (a >= 0.5)
{
return s * 0.5 * log1p (2 * a / (1 - a));
}
else if (a > GSL_DBL_EPSILON)
{
return s * 0.5 * log1p (2 * a + 2 * a * a / (1 - a));
}
else
{
return x;
}
}
下面给个测试代码:
#include <iostream>
#include "complex.h"
using namespace std;
int main()
{
Complex z(1, 2);
cout << z << endl;
cout << z.conjugate() << endl;
cout << -z << endl;
cout << z + Complex(3, 4) << endl;
cout << z - Complex(3, 4) << endl;
cout << z * Complex(3, 4) << endl;
cout << z / Complex(3, 4) << endl;
z = Complex(3, 4);
cout << z << endl;
cout << z.inverse() << endl;
cout << "Hello World!" << endl;
cout << sqrt(Complex(3, 4)) << endl;
cout << exp(Complex(3, 4)) << endl;
cout << pow(Complex(3, 4), Complex(1, 2)) << endl;
cout << pow(Complex(3, 4), 6) << endl;
cout << log(Complex(3, 4), 6) << endl;
cout << sin(Complex(3, 4)) << endl;
cout << arcsin(Complex(3, 4)) << endl;
cout << polar(1, 3.14159265358979 / 4) << endl;
cout << arcsinh(Complex(3, 4)) << endl;
cout << arccosh(Complex(3, 4)) << endl;
cout << arctanh(Complex(3, 4)) << endl;
cout << arcsech(Complex(3, 4)) << endl;
z = 2;
cout << z << endl;
return 0;
}