hdu 3903 Trigonometric Function （数学题）

Trigonometric Function

                                                                                Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 125536/65536 K (Java/Others)

Problem Description

Give you a triangle ABC. Get more information in the picture below.

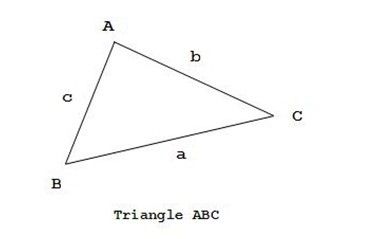
Now, give you 6 integers a, b, c, n, m and k. a, b and c are triangle ABC`s three edges. Can you judge whether the result of the following fraction is rational number?

 

Input

There are several test cases in the input data.
Each case is just one line with 6 integers -- a, b, c, n, m, k (0< a, b, c, n, m, k < 10^4) separated by spaces. The input data ensures that sin(kC) will not be equal with 0.

 

Output

Each case output “YES”, if the result of the fraction is rational number, otherwise “NO”.

 

Sample Input

   
   
   
   

    
    
    
    2
1 1 1 1 1 1
3 4 5 6 7 7
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    NO
YES
   
   
   
   

 

昨天比赛的一道题，卡在这道题好长时间也没做出来。

题意：给出三角形的三条边a、b、c和三个参数n、m、k。问

是不是一个有理数，其中A、B、C为三角形的三个内角。

我做的时候只考虑了特殊角，通过枚举nA+mB的值和kC的值来判断，一直WA。

比赛完上网搜了一下解题报告，没想到思路就是错的。

首先应该明白这些：

（1）若cosA 为有理数，n 为整数，则cos(nA)也为有理数。

（2）若sinA 为有理数，则sin(nA) = u*sinA，其中u 为有理数，那么sin(nA)也是有理数。

由此可得分子为有理数，所以只需要判断分母是不是有理数即可，即只需要判断sinC是不是有理数即可。

利用余弦定理可以求出cosC=（a^2+b^2-c^2)/(2ab),然后根据(cosC)^2 + (sinC)^2 = 1,可以得到

sinC * (2ab)= sqrt(4*a^2*b^2 - (a^2 + b^2 - c^2)*(a^2 + b^2 - c^2))。

所以只要4*b^2*c^2 - (a^2 + b^2 - c^2)*(a^2 + b^2 - c^2)是一个平方数，开方以后sinC就是一个有理数，否则就是无理数。

#include<stdio.h>
#include<math.h>
int main()
{
    __int64 t, a, b, c, n, m, k;
    scanf("%I64d",&t);
    while(t--)
    {
        scanf("%I64d%I64d%I64d%I64d%I64d%I64d",&a,&b,&c,&n,&m,&k);
        __int64 s = 4 * a * a * b * b - (a * a + b * b - c * c) * (a * a + b * b - c * c);
        __int64 tmp = sqrt(s);
        if(tmp * tmp == s)
            printf("YES\n");
        else
            printf("NO\n");
    }
    return 0;
}