Ng机器学习系列补充:3、关联分析算法Apriori
机器学习补充系列国际权威的学术组织the IEEE International Conference on Data Mining (ICDM,国际数据哇局会议) 2006年12月评选出了数据挖掘领域的十大经典算法:C4.5, k-Means, SVM, Apriori, EM, PageRank, AdaBoost, kNN, Naive Bayes, and CART,它们在数据挖掘领域都产生了极为深远的影响,这里对他们做一个简单介绍,仅作为对Ng机器学习教程的补充。
由于k-Means、SVM、EM、kNN、Naive Bayes在Ng的系列教程中都有涉及,所以此系列教程只涉及决策树算法C4.5、关联规则算法Apriori、网页排名算法PageRank、集成学习算法AdaBoost(Adaptive Boosting,自适应推进)、分类与回归树算法CART(Classification and Regression Trees);另外会加上对神经网络的BP算法介绍,后续也会考虑介绍遗传算法等内容。
1)名词解释
2)Apriori算法举例说明
1)名词解释
Apriori algorithm是关联规则里一项基本算法,也被称为购物蓝分析 (Market Basket analysis),因为“购物蓝分析”很贴切的表达了适用该算法情景中的一个子集。关于这个算法有一个非常有名的故事:"尿布和啤酒"。故事是这样的:美国的妇女们经常会嘱咐她们的丈夫下班后为孩子买尿布,而丈夫在买完尿布后又要顺手买回自己爱喝的啤酒,因此啤酒和尿布在一起被购买的机会很多。这个举措使尿布和啤酒的销量双双增加,并一直为众商家所津津乐道。
数据集:存储着二维结构的记录集。比如所有的交易记录。
记录:数据集中的一行。比如一条交易记录。
项:比如每一个商品就表示一项。
项集(Itemset):某些项的集合。比如3号商品和5号商品就表示一个项集{3号商品,5号商品}。
一个项集的支持度(Support):绝对支持度,数据集中包含该项集的记录数;相对支持度,数据集中包含该项集的记录数占所有记录数的比例。比如共有100条交易记录,其中有9条交易记录中同时买了3号商品和5号商品,就认为项集 {3号商品,5号商品} 的绝对支持度为9,相对支持度为9%。
最小支持度(Minimum Support):根据实际问题人为定义,比如22%等。小于该支持度的项集认为是无效数据,比如100个人中买3号商品的有78个,买5号商品的有36个,都大于22,则认为项集 {3号商品} 和 项集{5号商品} 都是有意义的,但项集 {3号商品,5号商品} 对问题的研究就没有意义,是无效数据了。
频繁项集(Frequent itemset):支持度大于等于最小支持度的项集,直观理解就是指经常出现在一块的物品的集合。比如项集 {3号商品} 和 项集{5号商品}都是频繁项集。注意,频繁集的子集一定是频繁集。反过来说,如果一个项集是非频繁的,那么它的所有超集也是非频繁的。
候选项集(Candidate itemset):通过向下合并得出的项集。所谓的向下合并,就是指合并频繁项集 {3号商品} 和 {5号商品}得到候选项集 {3号商品,5号商品},该项集有效无效,要通过判断该项集的支持度来决定,所以称为候选项集。
可信度或置信度(Confidence): 针对一条诸如{尿布}->{葡萄酒}的关联规则来定义的,定义为 Confidence(X->Y) = Support(X ∩ Y) / Support(X) = P(Y|X)。也就是说买了尿布和葡萄酒的人占已经买了尿布的人的比例,这就是X推荐Y的置信度Confidence(X->Y)。
提升度(Lift):Lift(X -> Y) =Lift(Y -> X) = Confidence(X -> Y) / Support(Y) = Confidence(Y -> X) / Support(X) = P(X and Y)/(P(X)P(Y))
Apriori算法主要包括发现频繁项集和挖掘关联规则这两步,其核心是:先找项数为1的频繁项集,在这基础上找项数为2的频繁项集、、、在项数为k的频繁项集中找项数为k+1的频繁项集。可能产生大量的候选项集以及可能需要重复扫描数据库是Apriori算法的两大缺点。
2)Apriori算法举例说明
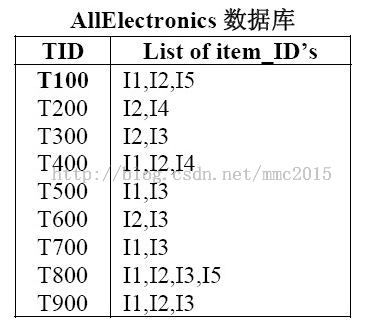
原始交易记录如下:
每一行表示一条交易,共有9笔交易,左边表示交易ID,右边表示商品ID。假设在我们的问题中,最小支持度是22%,那么每件商品至少要出现9*22%=2次才算频繁。
第一次扫描数据库,使得在每一条交易中,右边的商品按ID增序排列,即上图不变。
第二次扫描数据库,找项数为1的频繁项集有:
左边表示商品ID,右边表示所有的交易记录中出现对应商品ID的记录数,且保证要大于阈值2。
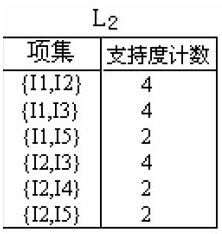
第三次扫描数据库,在 项数为1的频繁项集 的基础上找 项数为2的频繁项集,方法是两两任意组合:
这里{I1,I4},{I3,I4},{I3,I5},{I4,I5}出现的次数都小于2,过滤掉,实际 项数为2的频繁项集 有:
在这基础上找 项数为3的频繁项集,此时就有规律性了,在 项数为k的频繁项集 上找 项数为k+1的频繁项集 的方法是:假如共有N个 项数为k的频繁项集,两两组合,满足两两中前K-1个商品ID相同,仅最后一个商品ID要求前一条记录的商品ID小于后一条记录的商品ID,求它们的并集得到 项数为k的频繁项集,那么最多共有![]() 种可能的组合:
种可能的组合:
上面得到的项集只能称为候选项集,还需要进一步确认其支持度是否大于等于22%(即出现次数大于2),分两步:
第一步是依次扫描数据库检验每一个候选项集出现的次数是否大于2,但如果N很大的话,![]() 将非常大,这就要用到Apriori算法的核心:项数为k+1的频繁项集 中的任意k个商品ID组成的子集也是频繁项集。对于每一个K+1个商品ID组成的候选项集 的所有长度为K的子集两两组合,共有
将非常大,这就要用到Apriori算法的核心:项数为k+1的频繁项集 中的任意k个商品ID组成的子集也是频繁项集。对于每一个K+1个商品ID组成的候选项集 的所有长度为K的子集两两组合,共有![]() 种组合,在项数为k的频繁项集中匹配,只要有一个组合没有找到就删除该K+1个商品ID组成的候选项集。例如第一条候选项集{I1,I2,I3},它的项数为2的频繁项集有:
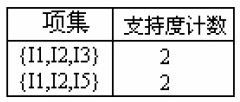
种组合,在项数为k的频繁项集中匹配,只要有一个组合没有找到就删除该K+1个商品ID组成的候选项集。例如第一条候选项集{I1,I2,I3},它的项数为2的频繁项集有:![]() 种,分别是{I1,I2},{I1,I3},{I2,I3},幸好这三种情况在项数为2的频繁项集中都找到了,所以保留候选项集{I1,I2,I3};但对于选项集{I1,I3,I5},它的项数为2的频繁项集有:{I1,3},{I1,I5},{I3,I5},由于在项数为2的频繁项集中都找不到{I3,I5},所以说要删除候选项集{I1,I3,I5}。通过这步确认,得到的依旧是准频繁项集(候选项集),它们是:
种,分别是{I1,I2},{I1,I3},{I2,I3},幸好这三种情况在项数为2的频繁项集中都找到了,所以保留候选项集{I1,I2,I3};但对于选项集{I1,I3,I5},它的项数为2的频繁项集有:{I1,3},{I1,I5},{I3,I5},由于在项数为2的频繁项集中都找不到{I3,I5},所以说要删除候选项集{I1,I3,I5}。通过这步确认,得到的依旧是准频繁项集(候选项集),它们是:
因为{I1,I2,I4}只出现了1次,小于最小支持度2,删除。就这个例子而言,它的最大频繁项集只有3,任何项数为4的候选项集的支持度都小于22%。
可见Apriori算法有个最大的问题就是要产生大量的候选项集,效率不高,并且要多次扫描数据库,在下一篇的PF_growth算法将避免了这两个个问题。
参考:
http://blog.sina.com.cn/s/blog_6e85bf420100ogn2.html
http://www.cnblogs.com/gaizai/archive/2010/03/31/1701573.html
http://blog.csdn.net/lu597203933/article/details/39159685
http://blog.csdn.net/aladdina/article/details/4141101