（子）图同构算法VF2实现（1）

子图同构问题本质上就是一种匹配，VF2算法加了很多feasibility rules，保证了算法的高效性。这里只是实现最基本的判断子图同构的算法：

参考文献有（其实google一把就能出来这些）：

http://stackoverflow.com/questions/8176298/vf2-algorithm-steps-with-example

http://www.zhihu.com/question/27071897

https://github.com/fozziethebeat/S-Space/tree/master/src/main/java/edu/ucla/sspace/graph/isomorphism

http://stackoverflow.com/questions/6743894/any-working-example-of-vf2-algorithm/6744603

Luigi P. Cordella,Pasquale Foggia,Carlo Sansone,Mario Vento: A (Sub)Graph Isomorphism Algorithm for Matching Large Graphs.IEEE Trans. Pattern Anal. Mach. Intell. 26(10): 1367-1372 (2004)

第一个链接给了一个示例：

http://stackoverflow.com/questions/8176298/vf2-algorithm-steps-with-example：

I will try to give you a quick explaination of my previous answer to this question :

Any working example of VF2 algorithm?

I will use the same example as the one in my previous answer :

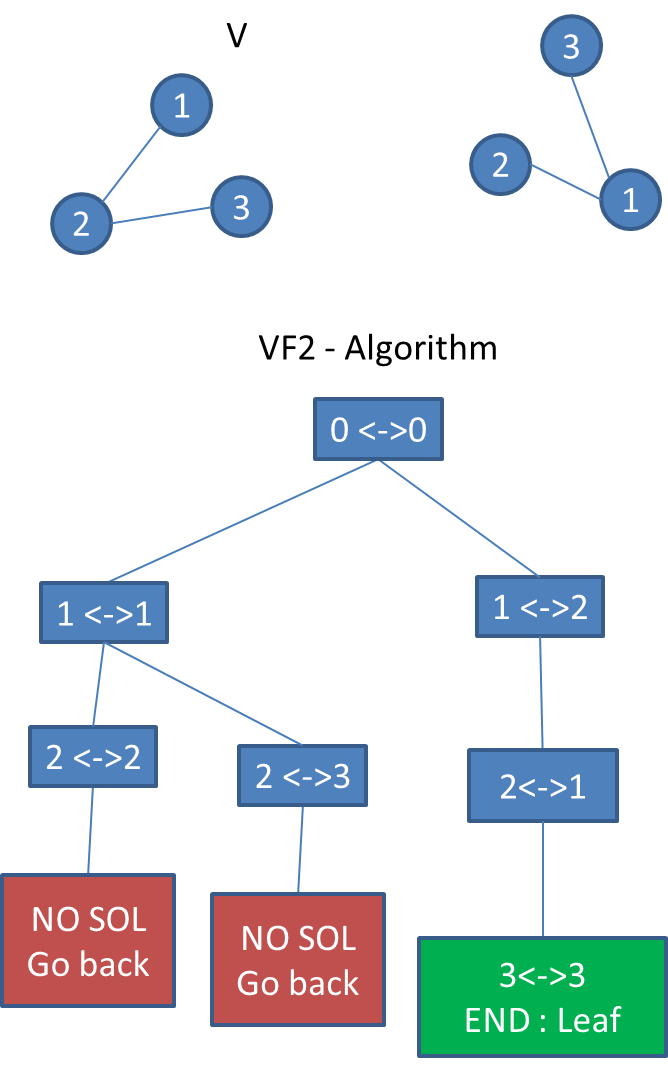
The 2 graphs above are V and V' .(V' is not in the drawing but it's the one on the right)

The VF2 algorithm is described in the graph.

Step by step

I want to know if V and V' are isomorphic.

I will use the following notations : XV is the node X in V

In the VF2 algoritm I will try to match each node in V with a node in V'.

step 1 :

I match empty V with empty V' : it always works

step 2 : I can match 1V with 1V',2V' or 3V'

I match 1V witch 1V' : it always works

step 3 :

I can match 2V with 2V' or 3V'

I match 2V with 2V' : it works because {1V 2V} and {1V' 2V} are isomorphic

step 4 :

I try to match 3V with a node in V' : I cannot! {it would be possible if their was an edge between node 3 and 2 in V', and no edge between 3 and 1)

So I go back to step 2

step 5:

I match 2V with 3V'

step 6:

same as step 4

I go back to step 2. there is no solution in step 2 , I go back to step 1

step 7:

I match 1V with 2V'

step 8:

I match 2V with 1V'

step 9 :

I match 3V with 3V'

it works I matched {1V 2V 3V} with { 2V' 1V' 3V'}

The graphs are isomorphic.

If I test all the solution and it never works the graph would not be isomorphic.

Hope this helps

About you're question on "matching", have a look at the wikipedia article on graph isomorphis :

http://en.wikipedia.org/wiki/Graph_isomorphism

this is a good example of a function f that matches graph G and H :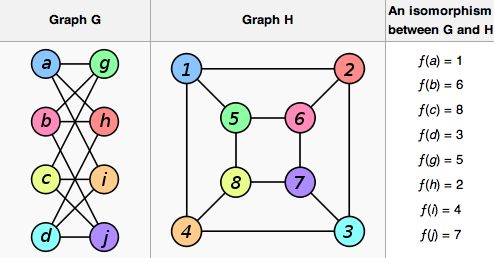 

Hope you can better understand this algorithm with this illustration.

下面给出我的算法设计（这里考虑边和点除了ID之外，还有label）：

边和图结构：

struct EDGE
{
	int id2;
	int label;
	EDGE(int _id2, int _label)
	{
		id2=_id2;
		label=_label;
	}
};


//邻接链表结构，不过是用vector来实现
struct GRAPH
{
	int graphID;
	vector<int> vID;
	vector<int> vLabel;


	vector<vector<EDGE> > vAdjacencyEdge;
	//外面的大vector< >，为每一个节点保存一个邻接表，一个图中有多少个节点，vAdjacencyEdge的size就是多少
	//vector<EDGE>存放EDGE[id2,label]组元，表示每个节点对应的兄弟节点id以及这两个节点间的边的label，
	//vector<EDGE>大小由每个节点的兄弟数量决定（这里所谓的兄弟，就是指“邻接点”）
	//因为可行pair(m,n)就是从当前状态M(s)的邻接点中寻找的，所以该结构能够加快搜索速度
};

每一个match结构：

//match结构，对应论文中提到的core_1 and core_2,
//whose dimensions correspond to the number of nodes in G1 and G2
struct MATCH
{
	//int *dbMATCHqu; //存储DB中的节点id和与之match的QU中的节点id
	//int *quMATCHdb; //存储QU中的节点id和与之match的DB中的节点id
	//使用map编程更方便，查找速度更快!
	map<int, int> dbMATCHqu;
	map<int, int> quMATCHdb;
};

从文件中读取数据（主要是保证每个点的邻接边/点能够按照struct GRAPH正确存储）：

vector<GRAPH *> ReadGraph(const char *filename)
{
	FILE *fp = fopen(filename, "r");
	/*
	if (!fp)
	{
		printf("fp is NULL, file [%s] doesn't exist...\n", filename);
		return;
	}
	*/

	EDGE e(-1,-1);
	vector<EDGE> v;
	v.push_back(e);

	char mark[2];
	int id,label,id2;
	vector<GRAPH *> gSet;
	GRAPH * g = NULL;
	while(true)
	{
		fscanf(fp, "%s", mark);
		if(mark[0]=='t')
		{
			
			fscanf(fp, "%s%d", mark, &id);
			if(id==-1)
			{
				gSet.push_back(g);
				break;
			}
			else //if input not ending, then
			{				
				if(g!=NULL)
				{
					gSet.push_back(g);
				}
				g = new GRAPH;
				g->graphID=id;
			}
		}
		else if(mark[0]=='v')
		{
			fscanf(fp, "%d%d", &id, &label);
			g->vID.push_back(id);
			g->vLabel.push_back(label);

			g->vAdjacencyEdge.push_back(v);//为每个节点申请一个vAdjacencyEdge，其中v只是占用位置，没有任何用处！
		}
		else if(mark[0]=='e')
		{
			fscanf(fp, "%d%d%d", &id, &id2, &label);

			e.id2=id2; e.label=label;
			g->vAdjacencyEdge[id].push_back(e);//id->id2的边
			e.id2=id; e.label=label;
			g->vAdjacencyEdge[id2].push_back(e);//id2->id的边
		}
	}

	fclose(fp);
	printf("graph number:%d\n", gSet.size());
	return gSet;

}

判断一个候选pair是否满足feasibility rules：

//其实 pair(quG->vID[i], dbG->vID[j])就是一个候选pair candidate
//判断该候选pair是否满足feasibility rules
bool FeasibilityRules(GRAPH *quG, GRAPH *dbG, MATCH match, int quG_vID, int dbG_vID)
{
	int quVid,dbVid,quGadjacencyEdgeSize,dbGadjacencyEdgeSize,i,j;
	bool flag=false;

	//首先，判断quG_vID和dbG_vID对应的label是否相同
	if(quG->vLabel[quG_vID]!=dbG->vLabel[dbG_vID]) //如果两个点的label不同，则【一定不】满足feasibility rules
	{
		return false;
	}
	
	//其次，判断是不是每次match的第一个比较pair
	if(match.quMATCHdb.size()==0) //如果是第一个比较pair
	{
		//只需要这两个点的label相同（已经判断成立了）即满足feasibility rules
		return true;
	}

	//最后（label相同，不是第一个pair【即，之前已经match了一部分节点】），那么只要下面条件成立就能满足最简单的feasibility rules：
	//1）quG_vID和dbG_vID与已经match的那些节点对中的【至少】一对(quVid,dbVid)分别相邻（quG_vID和dbG_vID分别是已经match的节点quVid和dbVid的“neighbor节点”）
	//2）如果存在多个相邻对(quVid,dbVid)，则必须要求【所有的】邻接边对( edge(quG_vID,quVid), edge(dbG_vID,dbVid) )的label一样
	for(map<int, int>::iterator iter=match.quMATCHdb.begin();iter!=match.quMATCHdb.end();iter++) //遍历所有的已经match的节点对
	{
		quVid=iter->first;
		quGadjacencyEdgeSize=quG->vAdjacencyEdge[quVid].size();
		for(i=1;i<quGadjacencyEdgeSize;i++) //从1开始依次扫描quVid的邻接点，第0个存的是(-1,-1)
		{
			//quG_vID是已经match的quG中的节点quVid的“第i个neighbor节点”
			if( quG->vAdjacencyEdge[quVid][i].id2==quG_vID ) 
			{
				dbVid=iter->second;
				dbGadjacencyEdgeSize=dbG->vAdjacencyEdge[dbVid].size();
				for(j=1;j<dbGadjacencyEdgeSize;j++) //从1开始依次扫描dbVid的邻接点，第0个存的是(-1,-1)
				{
					//同时，与quVid相match的节点dbVid在dbG中的“第j个neighbor节点”正好是dbG_vID
					if( dbG->vAdjacencyEdge[dbVid][j].id2==dbG_vID )
					{
						//判断2）是否成立
						if( quG->vAdjacencyEdge[quVid][i].label != dbG->vAdjacencyEdge[dbVid][j].label )
						{
							//因为2）要求【所有的】label一样，只要有一个不一样，则返回false
							return false;
						}
						else
						{
							//标记：flag=true表示至少有一对满足1）的pair(dbVid,quVid)，同时满足了2）
							//因为有可能循环结束了，在所有的已经match的节点对里，找不到一个pair(dbVid,quVid)同时满足条件1）和2）
							flag=true;
						}
					}
				}
			}
		}
	}
	return flag;
}

最后给出该算法的伪代码：